10.2 直方图(基础讲解)(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
10.2 直方图
【学习目标】
1. 会正确列出一组数据的制作频数分布表,并据此绘制频数分布直方图;
2. 理解频数分布直方图的意义和作用.
【知识总结】
一、组距与频数分布表的概念
1.组距:每个小组的两个端点之间的距离(组内数据的取值范围).
2.频数分布表:把各个类别及其对应的频数用表格的形式表示出来,所得表格就是频数分布表.
1. 频数分布直方图的画法
制作频数分布直方图的一般步骤是:
(1)找出所给数据中的最大值和最小值,确定统计量的范围;
(2)确定组数和组距(每组两个端点之间的距 ( http: / / www.21cnjy.com )离叫组距)进行分组. 数据个数在 100 以内,一般分 5 到 12 组. 为了使每个数据都落在相应的组内,可以把第一组的起点略微减小一点; 21教育网
(3)统计每组中数据出现的次数(这个次数被称为频数);
(4)根据分组和频数,绘制频数分布直方图
用小长方形的高直接表示频数的分布.
2.直方图和条形图的联系与区别:
(1)联系:它们都是用矩形来表示数据分布情况的;当矩形的宽度相等时,都是用矩形的高来表示数据分布情况的;www.21-cn-jy.com
(2)区别:由于分组数据 ( http: / / www.21cnjy.com )具有连续性,直方图中各矩形之间通常是连续排列,中间没有空隙,而条形图中各矩形是分开排列,中间有一定的间隔;直方图是用面积表示各组频数的多少,而条形图是用矩形的高表示频数. 【来源:21·世纪·教育·网】
二、频数分布折线图
频数分布折线图的制作一般都是在频数分布直方图的基础上得到的,
具体步骤是:①取直方图中每一个长方形上边 ( http: / / www.21cnjy.com )的中点;②再在横轴上取两个频数为0的点(直方图最左及最右两边各取一个,它们分别与直方图左右相距半个组距);③再将这些点用线段依次连接起来,得到了频数分布折线图.21·世纪*教育网
【典型例题】
【类型】一、组距、频数与频数分布表的概念
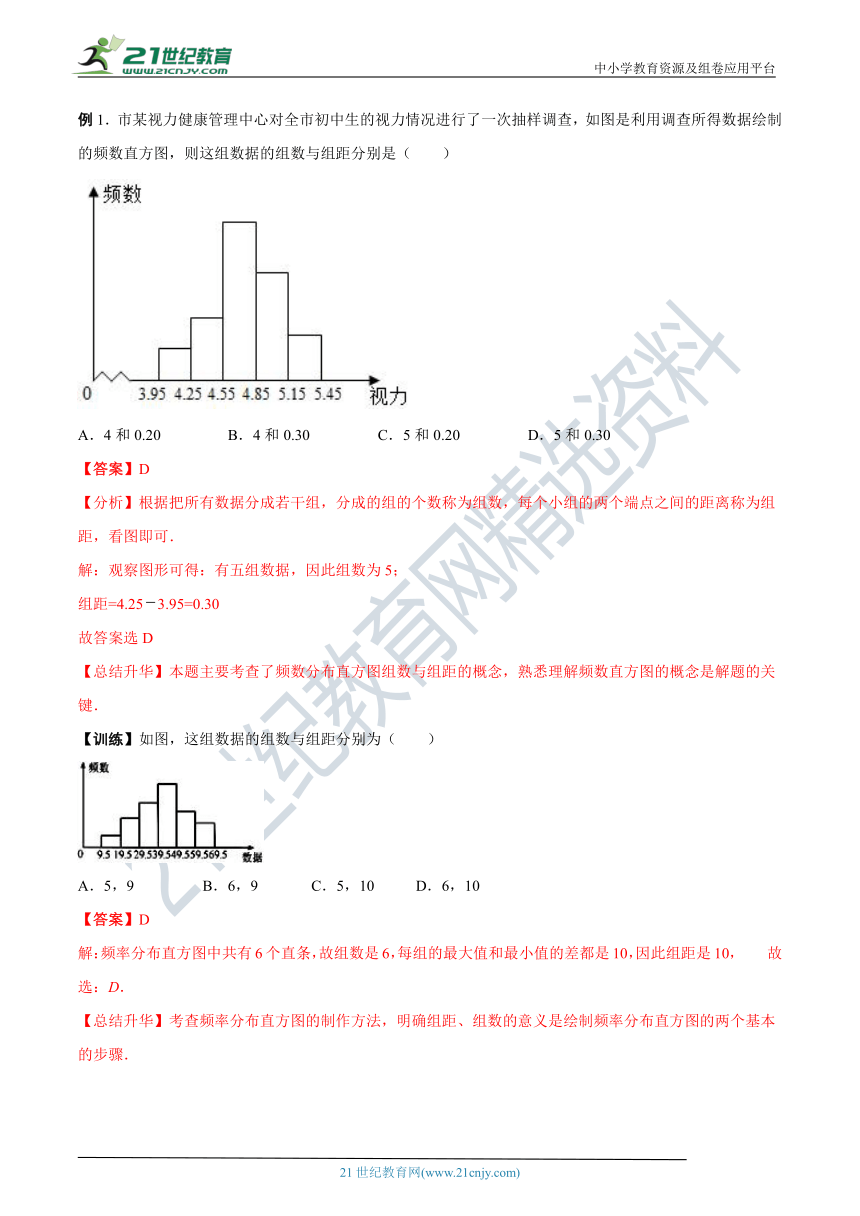
例1.市某视力健康管理中心对全 ( http: / / www.21cnjy.com )市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
【答案】D
【分析】根据把所有数据分成若干组,分成的组的个数称为组数,每个小组的两个端点之间的距离称为组距,看图即可.2-1-c-n-j-y
解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
【总结升华】本题主要考查了频数分布直方图组数与组距的概念,熟悉理解频数直方图的概念是解题的关键.
【训练】如图,这组数据的组数与组距分别为( )
( http: / / www.21cnjy.com / )
A.5,9 B.6,9 C.5,10 D.6,10
【答案】D
解:频率分布直方图中共有6个直条,故组数是6,每组的最大值和最小值的差都是10,因此组距是10, 故选:D.
【总结升华】考查频率分布直方图的制作方法,明确组距、组数的意义是绘制频率分布直方图的两个基本的步骤.
个人旅游年 消费金额/元
频数
【训练】2016年4月30日至5 ( http: / / www.21cnjy.com )月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )【来源:21cnj*y.co*m】
A.小王随机抽取了100名员工 B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
【答案】C
解:A、小王随机抽取了12+25+31+22+10=100人,故正确;
B、观察统计表发现频数分布表中,组距是2000,组数是5组,故正确;
C、个人旅游消费金额在6000元以上的人数占随机抽取人数的,故错误;
D、在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有25+12=37人,故正确;
故选:C.
【总结升华】本题考查了频数分布表的知识,解题的关键是能够仔细读表并从中进一步整理出解题的有关信息,难度不大.
【类型】二、频数分布表或直方图
例2.随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60 0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
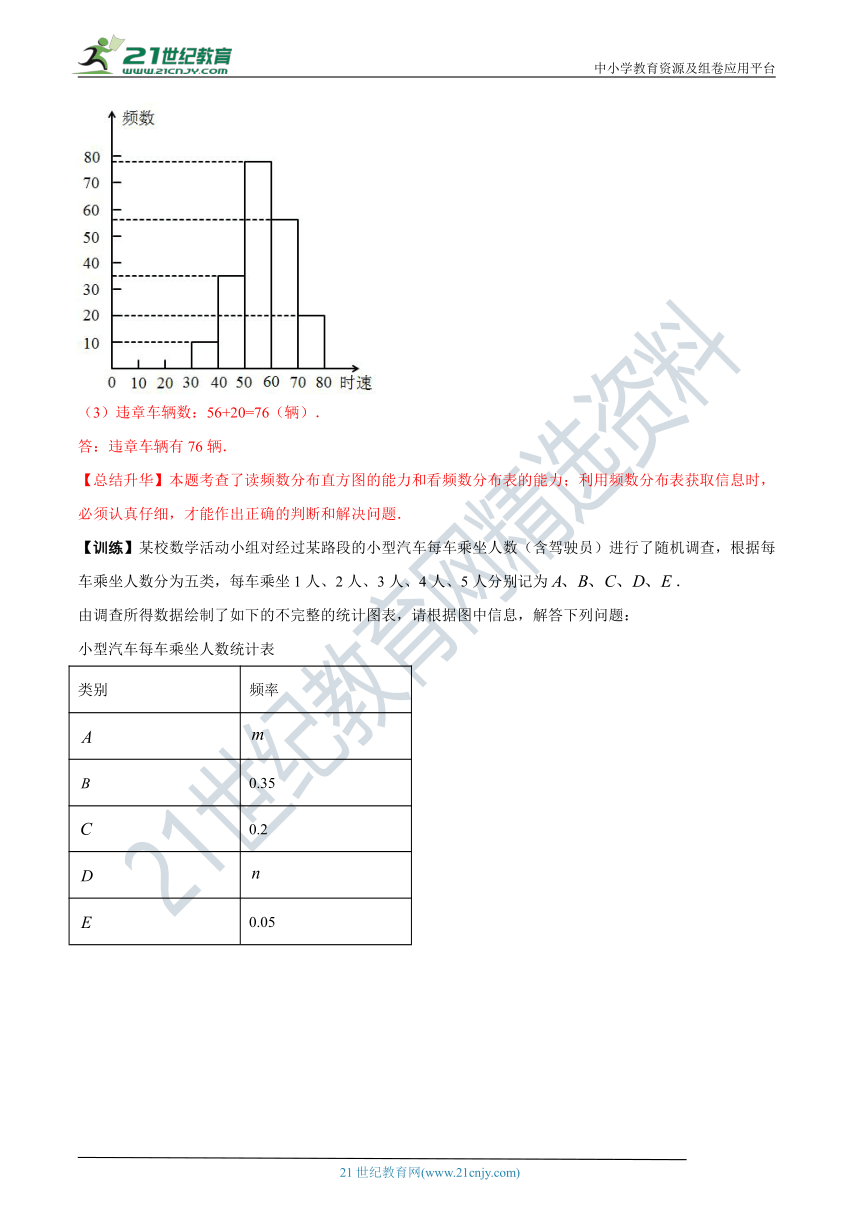
( http: / / www.21cnjy.com / )
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
【答案】(1)第二行0.18,第三行78,第四行0.28;(2)见解析;(3)76
【分析】
(1)根据频数÷总数=频 ( http: / / www.21cnjy.com )率进行计算即可;
(2)结合(1)中的数据补全图形即可;
(3)根据频数分布直方图可看出汽车时速不低于60千米的车的数量.21cnjy.com
(1)解:(1)36÷200=0.18,
200×0.39=78,
200-10-36-78-20=56,
56÷200=0.28;
故第二行0.18,第三行78,第四行0.28
(2)如图所示
( http: / / www.21cnjy.com / )
(3)违章车辆数:56+20=76(辆).
答:违章车辆有76辆.
【总结升华】本题考查了读频数分布直方图的能力和看频数分布表的能力;利用频数分布表获取信息时,必须认真仔细,才能作出正确的判断和解决问题.
【训练】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为五类,每车乘坐1人、2人、3人、4人、5人分别记为.
由调查所得数据绘制了如下的不完整的统计图表,请根据图中信息,解答下列问题:
小型汽车每车乘坐人数统计表
类别 频率
0.35
0.2
0.05
( http: / / www.21cnjy.com / )
(1)求本次调查的小型汽车数量.
(2)求的值.
(3)补全条形统计图.
解:(1)(辆),
所以本次调查的小型汽车数量为160辆;
(2),
;
(3)类小汽车的数量为类小汽车的数量为.
补全条形统计图如下:
( http: / / www.21cnjy.com / ) .
【总结升华】本题考查了条形统计图和频率分布表,从条形统计图和频率分布表中获取所需信息是解答本题的关键.21世纪教育网版权所有
【类型】三、频数分布折线图
例3.抽样检查40个工件的长度,收集到如下一组数据(单位:cm):
23.26 23.27 23.52 23.51 23.43 23.42 23.54 23.55 23.6621*cnjy*com
23.67 23.31 23.30 23.27 23.28 23.41 23.40 23.55 23.56【出处:21教育名师】
23.44 23.43 23.38 23.39 23.63 23.64 23.54 23.56 23.462·1·c·n·j·y
23.44 23.48 23.46 23.50 23.53 23.55 23.46 23.44 23.45【版权所有:21教育】
23.47 23.49 23.50 23.46
试列出这组数据的频数分布表.画出频数分布直方图和频数折线圈.
【分析】利用频数分布直方图画频数折线 ( http: / / www.21cnjy.com )图时,折线图的两个端点要与横轴相交,其方法是在直方图的左右两边各延伸一个假想组,并将频数折线两端连接到轴两端假想组的组中点,就形成了频数折线图.
【答案与解析】
解:列频数分布表如下:
( http: / / www.21cnjy.com / )
根据上表,画出频数分布直方图;连接各小长方形上面一条边的中点及横轴上距直方图左右相距半个组距的两个频数为0的点得到频数折线图(如图所示).21·cn·jy·com
( http: / / www.21cnjy.com / )
【总结升华】本例分组采用了“每组端点比数据多 ( http: / / www.21cnjy.com )一位小数”,即第一组的起点比数据的最小值再小一点的方法.体会这种分组方法的优势,对我们今后的学习很有帮助.21教育名师原创作品
【类型】四、综合应用
例4.为庆祝中华人民共和国成立70周 ( http: / / www.21cnjy.com )年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
( http: / / www.21cnjy.com / )
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人
【答案】(1)40;(2);(3)见解析;(4)估计身高在的学生约有80人
【分析】
(1)用A组人数×其所占的百分数即可得到结论;
(2)利用乘以对应的比例即可求解;
(3)根据题意补全频数分布直方图即可;
(4)利用总人数400乘以对应的比例.
解:(1)这次抽样调查,一共抽取学生(人);
(2)扇形统计图中,扇形E的圆心角度数是,
故答案为:40;;
(3)身高在的人数为:人,
补全频数分布直方图如图所示;
(4)(人),
答:估计身高在的学生约有180人.
( http: / / www.21cnjy.com / )
【总结升华】本题考查读频数分布直方图的能 ( http: / / www.21cnjy.com )力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察 分析 研究统计图,才能作出正确的判断和解决问题.21*cnjy*com
【训练】小明是一名健步走运动的爱好者,他用 ( http: / / www.21cnjy.com )手机软件记录了他近期健步走的步数(单位:万步),绘制出如下的统计图①和统计图②,请根据相关信息,解答下列问题:
( http: / / www.21cnjy.com / )
(Ⅰ)本次记录的总天数为_____________,图①中m的值为______________;
(Ⅱ)求小名近期健步走步数的平均数、众数和中位数;
(Ⅲ)根据样本数据,若小明坚持健步走一年(记为365天),试估计步数为1.1万步的天数.
解:(Ⅰ)2+5+7+8+3=25,100-32-28-20-8=12;
(Ⅱ)∵ =;
∴ 这组数据的平均数为1.22万步;
∵ 在这组数据中,1.3万步出现了8次,出现的次数最多;
∴ 这组数据的众数为1.3万步;
∵ 将这组数据按从小到大的顺序排列,其中处于中间的数是1.2万步;
∴ 这组数据的中位数为1.2万步;
(Ⅲ)∵在统计的健步走的步数样本数据中,步数为1.1万约占20%;
∴估计365天中,步数为1.1万约占20%;
365×20%=73;
答:若小明坚持健步走一年(记为365天),步数为1.1万步的天数约为
73天.
【总结升华】本题主要考查了通过扇形统计图和条形统计图中的数据求解众数、中位数、平均数,理解图表的意义很重要.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
10.2 直方图
【学习目标】
1. 会正确列出一组数据的制作频数分布表,并据此绘制频数分布直方图;
2. 理解频数分布直方图的意义和作用.
【知识总结】
一、组距与频数分布表的概念
1.组距:每个小组的两个端点之间的距离(组内数据的取值范围).
2.频数分布表:把各个类别及其对应的频数用表格的形式表示出来,所得表格就是频数分布表.
1. 频数分布直方图的画法
制作频数分布直方图的一般步骤是:
(1)找出所给数据中的最大值和最小值,确定统计量的范围;
(2)确定组数和组距(每组两个端点之间的距 ( http: / / www.21cnjy.com )离叫组距)进行分组. 数据个数在 100 以内,一般分 5 到 12 组. 为了使每个数据都落在相应的组内,可以把第一组的起点略微减小一点; 21教育网
(3)统计每组中数据出现的次数(这个次数被称为频数);
(4)根据分组和频数,绘制频数分布直方图
用小长方形的高直接表示频数的分布.
2.直方图和条形图的联系与区别:
(1)联系:它们都是用矩形来表示数据分布情况的;当矩形的宽度相等时,都是用矩形的高来表示数据分布情况的;www.21-cn-jy.com
(2)区别:由于分组数据 ( http: / / www.21cnjy.com )具有连续性,直方图中各矩形之间通常是连续排列,中间没有空隙,而条形图中各矩形是分开排列,中间有一定的间隔;直方图是用面积表示各组频数的多少,而条形图是用矩形的高表示频数. 【来源:21·世纪·教育·网】
二、频数分布折线图
频数分布折线图的制作一般都是在频数分布直方图的基础上得到的,
具体步骤是:①取直方图中每一个长方形上边 ( http: / / www.21cnjy.com )的中点;②再在横轴上取两个频数为0的点(直方图最左及最右两边各取一个,它们分别与直方图左右相距半个组距);③再将这些点用线段依次连接起来,得到了频数分布折线图.21·世纪*教育网
【典型例题】
【类型】一、组距、频数与频数分布表的概念
例1.市某视力健康管理中心对全 ( http: / / www.21cnjy.com )市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
【答案】D
【分析】根据把所有数据分成若干组,分成的组的个数称为组数,每个小组的两个端点之间的距离称为组距,看图即可.2-1-c-n-j-y
解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
【总结升华】本题主要考查了频数分布直方图组数与组距的概念,熟悉理解频数直方图的概念是解题的关键.
【训练】如图,这组数据的组数与组距分别为( )
( http: / / www.21cnjy.com / )
A.5,9 B.6,9 C.5,10 D.6,10
【答案】D
解:频率分布直方图中共有6个直条,故组数是6,每组的最大值和最小值的差都是10,因此组距是10, 故选:D.
【总结升华】考查频率分布直方图的制作方法,明确组距、组数的意义是绘制频率分布直方图的两个基本的步骤.
个人旅游年 消费金额/元
频数
【训练】2016年4月30日至5 ( http: / / www.21cnjy.com )月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )【来源:21cnj*y.co*m】
A.小王随机抽取了100名员工 B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
【答案】C
解:A、小王随机抽取了12+25+31+22+10=100人,故正确;
B、观察统计表发现频数分布表中,组距是2000,组数是5组,故正确;
C、个人旅游消费金额在6000元以上的人数占随机抽取人数的,故错误;
D、在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有25+12=37人,故正确;
故选:C.
【总结升华】本题考查了频数分布表的知识,解题的关键是能够仔细读表并从中进一步整理出解题的有关信息,难度不大.
【类型】二、频数分布表或直方图
例2.随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60 0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
( http: / / www.21cnjy.com / )
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
【答案】(1)第二行0.18,第三行78,第四行0.28;(2)见解析;(3)76
【分析】
(1)根据频数÷总数=频 ( http: / / www.21cnjy.com )率进行计算即可;
(2)结合(1)中的数据补全图形即可;
(3)根据频数分布直方图可看出汽车时速不低于60千米的车的数量.21cnjy.com
(1)解:(1)36÷200=0.18,
200×0.39=78,
200-10-36-78-20=56,
56÷200=0.28;
故第二行0.18,第三行78,第四行0.28
(2)如图所示
( http: / / www.21cnjy.com / )
(3)违章车辆数:56+20=76(辆).
答:违章车辆有76辆.
【总结升华】本题考查了读频数分布直方图的能力和看频数分布表的能力;利用频数分布表获取信息时,必须认真仔细,才能作出正确的判断和解决问题.
【训练】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为五类,每车乘坐1人、2人、3人、4人、5人分别记为.
由调查所得数据绘制了如下的不完整的统计图表,请根据图中信息,解答下列问题:
小型汽车每车乘坐人数统计表
类别 频率
0.35
0.2
0.05
( http: / / www.21cnjy.com / )
(1)求本次调查的小型汽车数量.
(2)求的值.
(3)补全条形统计图.
解:(1)(辆),
所以本次调查的小型汽车数量为160辆;
(2),
;
(3)类小汽车的数量为类小汽车的数量为.
补全条形统计图如下:
( http: / / www.21cnjy.com / ) .
【总结升华】本题考查了条形统计图和频率分布表,从条形统计图和频率分布表中获取所需信息是解答本题的关键.21世纪教育网版权所有
【类型】三、频数分布折线图
例3.抽样检查40个工件的长度,收集到如下一组数据(单位:cm):
23.26 23.27 23.52 23.51 23.43 23.42 23.54 23.55 23.6621*cnjy*com
23.67 23.31 23.30 23.27 23.28 23.41 23.40 23.55 23.56【出处:21教育名师】
23.44 23.43 23.38 23.39 23.63 23.64 23.54 23.56 23.462·1·c·n·j·y
23.44 23.48 23.46 23.50 23.53 23.55 23.46 23.44 23.45【版权所有:21教育】
23.47 23.49 23.50 23.46
试列出这组数据的频数分布表.画出频数分布直方图和频数折线圈.
【分析】利用频数分布直方图画频数折线 ( http: / / www.21cnjy.com )图时,折线图的两个端点要与横轴相交,其方法是在直方图的左右两边各延伸一个假想组,并将频数折线两端连接到轴两端假想组的组中点,就形成了频数折线图.
【答案与解析】
解:列频数分布表如下:
( http: / / www.21cnjy.com / )
根据上表,画出频数分布直方图;连接各小长方形上面一条边的中点及横轴上距直方图左右相距半个组距的两个频数为0的点得到频数折线图(如图所示).21·cn·jy·com
( http: / / www.21cnjy.com / )
【总结升华】本例分组采用了“每组端点比数据多 ( http: / / www.21cnjy.com )一位小数”,即第一组的起点比数据的最小值再小一点的方法.体会这种分组方法的优势,对我们今后的学习很有帮助.21教育名师原创作品
【类型】四、综合应用
例4.为庆祝中华人民共和国成立70周 ( http: / / www.21cnjy.com )年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
( http: / / www.21cnjy.com / )
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人
【答案】(1)40;(2);(3)见解析;(4)估计身高在的学生约有80人
【分析】
(1)用A组人数×其所占的百分数即可得到结论;
(2)利用乘以对应的比例即可求解;
(3)根据题意补全频数分布直方图即可;
(4)利用总人数400乘以对应的比例.
解:(1)这次抽样调查,一共抽取学生(人);
(2)扇形统计图中,扇形E的圆心角度数是,
故答案为:40;;
(3)身高在的人数为:人,
补全频数分布直方图如图所示;
(4)(人),
答:估计身高在的学生约有180人.
( http: / / www.21cnjy.com / )
【总结升华】本题考查读频数分布直方图的能 ( http: / / www.21cnjy.com )力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察 分析 研究统计图,才能作出正确的判断和解决问题.21*cnjy*com
【训练】小明是一名健步走运动的爱好者,他用 ( http: / / www.21cnjy.com )手机软件记录了他近期健步走的步数(单位:万步),绘制出如下的统计图①和统计图②,请根据相关信息,解答下列问题:
( http: / / www.21cnjy.com / )
(Ⅰ)本次记录的总天数为_____________,图①中m的值为______________;
(Ⅱ)求小名近期健步走步数的平均数、众数和中位数;
(Ⅲ)根据样本数据,若小明坚持健步走一年(记为365天),试估计步数为1.1万步的天数.
解:(Ⅰ)2+5+7+8+3=25,100-32-28-20-8=12;
(Ⅱ)∵ =;
∴ 这组数据的平均数为1.22万步;
∵ 在这组数据中,1.3万步出现了8次,出现的次数最多;
∴ 这组数据的众数为1.3万步;
∵ 将这组数据按从小到大的顺序排列,其中处于中间的数是1.2万步;
∴ 这组数据的中位数为1.2万步;
(Ⅲ)∵在统计的健步走的步数样本数据中,步数为1.1万约占20%;
∴估计365天中,步数为1.1万约占20%;
365×20%=73;
答:若小明坚持健步走一年(记为365天),步数为1.1万步的天数约为
73天.
【总结升华】本题主要考查了通过扇形统计图和条形统计图中的数据求解众数、中位数、平均数,理解图表的意义很重要.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
