2.3圆周运动实例分析_(教科版必修2)

(共64张PPT)
第3节 圆周运动实例分析
一、水平面内的圆周运动
六、能力提升
二、火车转弯问题
三、圆周运动临界问题
四、离心运动
五、巩固练习
问题：“旋转秋千”中的缆绳跟中心轴的夹角与哪些因素有关？体重不同的人坐在秋千上旋转时，缆绳与中心轴的夹角相同吗？
一、水平面内的圆周运动
“旋转秋千”的运动经过简化，可以看做如下的物理模型：在一根长为l的细线下面系一根质量为m的小球，将小球拉离竖直位置，使悬线与竖直方向成α角，给小球一根初速度，使小球在水平面内做圆周运动，悬线旋转形成一个圆锥面，这种装置叫做圆锥摆。
例、小球做圆锥摆时细绳长l，与竖直方向成α角，求小球做匀速圆周运动的角速度ω。
O
mg
T
F
小球受力：
竖直向下的重力G
沿绳方向的拉力T
小球的向心力：
由T和G的合力提供
解：
l
小球做圆周运动的半径
由牛顿第二定律：
即：
r
α
由此可见，缆绳与中心轴的夹角跟“旋转秋千”的角速度和绳长有关，而与所乘坐人的体重无关，在绳长一定的情况下，角速度越大则缆绳与中心轴的夹角也越大。想一想，怎么样求出它的运动周期？
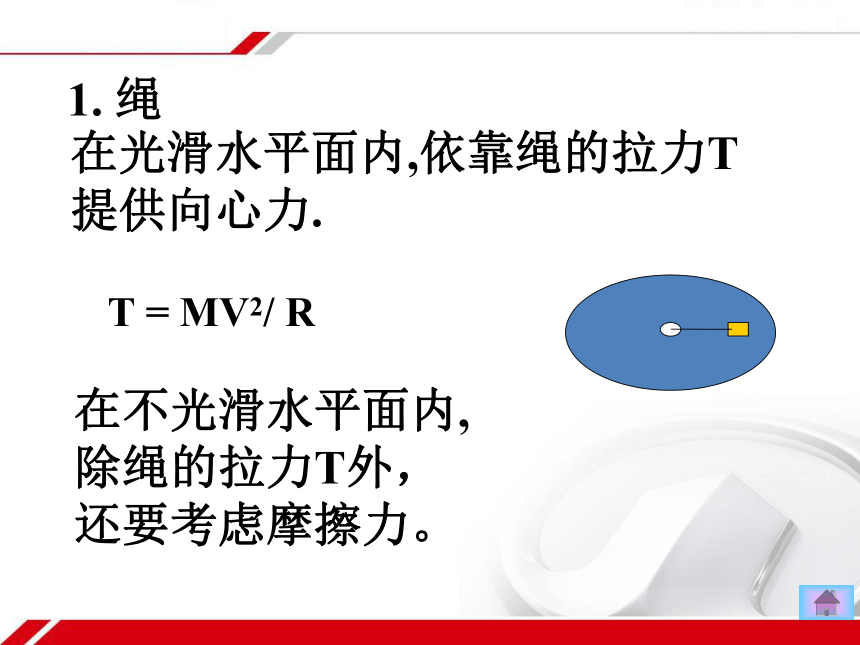
1. 绳
在光滑水平面内,依靠绳的拉力T提供向心力.
T = MV2/ R
在不光滑水平面内,除绳的拉力T外，还要考虑摩擦力。
2. 杆
例: 如图所示的两段轻杆OA和AB长分别为2L和L,在A和B两点分别固定有质量均为M的光滑小球, 当整个装置绕O点以ω做圆周运动时, 求OA和AB杆的张力各为多大
O
A
B
A
B
TAB
TOA
T`AB
解: 据题意, B球的向心力来源于AB杆对它的拉力TAB , 据牛顿第二定律:
TAB = 3M ω2 L ……(1 )
A球的向心力来源于OA杆与AB对它的作用力的合力 , 据牛顿第三定律:
TAB = T`AB ……. .(2)
据牛顿第二定律:对A球有
TOA - T`AB = M ω22L ….. (3)
解得: TOA = 5M ω2L
即:OA杆的张力为5M ω2L, AB杆的张力为3M ω2L .
3.弹簧
在光滑水平面内, 由弹簧的弹力F来提供向心力.
F = MV2/ R
O
例:劲度系数为K的弹簧,一端栓着质量为M的光滑小球,一端固定在水平面内,以角速度ω, 半径L做匀速圆周运动,求弹簧的原长.
据胡克定律: 有 F=K(L-L0 )
据牛顿第二定律: K(L-L0 ) = M ω2L
解得: L0 = L - M ω2 L/ K .
注意: 对于弹簧约束情况下的圆周运动, 一定要找准真实的圆周运动的半径与向心力.
L
L0
F
解:设弹簧的原长为L0 , 则弹簧的形变量为L-L0
例: A、B、C三物体放在水平圆台上,它们与平台的动摩擦因数相同,其质量之比为3:2:1,它们与转轴之间的距离之比为1:2:3,当平台以一定的角速度旋转时,它们均无相对滑动,它们受到静摩擦力分别为fA、fB、fC,则 ( )
A. fAfB>fC C. fA=fB解析:A、B、C三物体在转动过程中未发生滑动，故转台对物体提供的静摩擦力应等于它们作圆周运动需要的向心力，即f提供=f需要=fn=Mω2R.三物体绕同一轴转动，角速度相等，把质量和圆周运动的半径关系代入上式，比较可知fA=fCB
C
A
4. 摩擦力提供向心力
例: A、B、C三物体放在水平圆台上,它们与平台的动摩擦因数相同,其质量之比为3:2:1,它们与转轴之间的距离之比为1:2:3,当平台以一定的角速度旋转时,它们均无相对滑动,它们受到静摩擦力分别为fA、fB、fC,当平台旋转的角速度不断增大时，哪个物体最先相对平台滑动，哪个物体最后滑动
B
C
A
扩展：
分别比较AC、BC、AB谁先动
C最先、其次是B、最后是A
二、火车转弯问题：
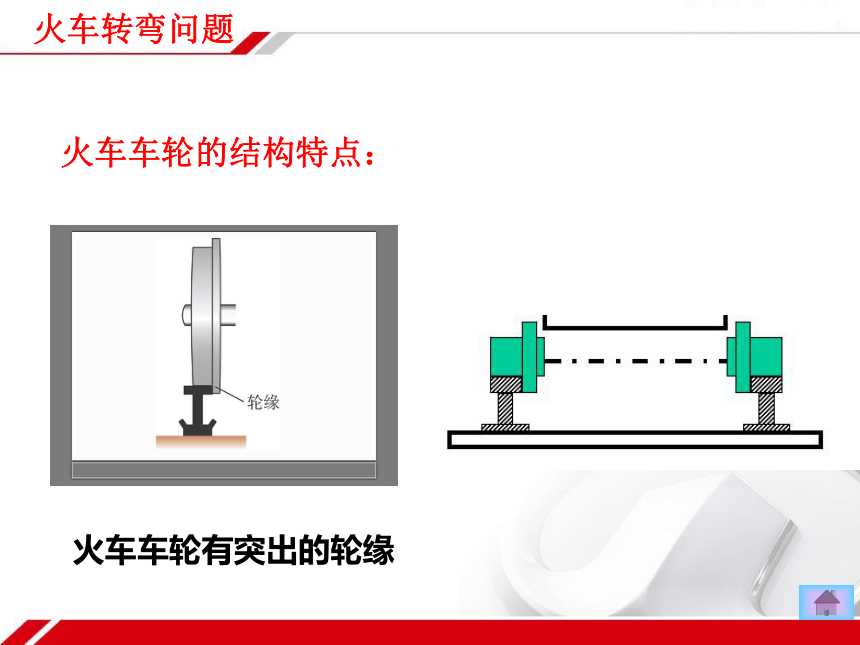
火车车轮的结构特点：
火车车轮有突出的轮缘
火车转弯问题
火车转弯
N
G
向右转
（1）火车转弯处内外轨无高度差
N
G
F
（1）火车转弯处内外轨无高度差
外轨对轮缘的弹力F就是使火车转弯的向心力
根据牛顿第二定律F=m 可知
R
V2
火车质量很大
外轨对轮缘的弹力很大
外轨和外轮之间的磨损大， 铁轨容易受到损坏
向右转
（2 ）转弯处外轨高于内轨
问题：设内外轨间的距离为L，内外轨的高度差为h，火车转弯的半径为R，则火车转弯的规定速度为v0 ？
F合=mgtanα≈mgsinα=mgh/L
由牛顿第二定律得：
F合=ma 所以mgh/L=
即火车转弯的规定速度
根据牛顿第二定律
α
N
G
F
α
1、在水平铁路转弯处，往往使外轨略高于内轨，这是为了( )
A．减轻火车轮子挤压外轨
B．减轻火车轮子挤压内轨
C．使火车车身倾斜，利用重力和支持力的合力提供转弯所需向心力
D．限制火车向外脱轨
ACD
三、圆周运动临界问题
问题1：汽车通过拱形桥时的运动可以看做圆周运动，质量为m的汽车以速度v通过拱形桥最高点时，若桥面的圆弧半径为R，则此时汽车对拱桥的压力为多大？
求汽车以速度v过半径为R的拱桥时对拱桥的压力？
【解】G和N的合力提供汽车做圆周运动的向心力，由牛顿第二定律得：
N
G
（ 1 ）由牛顿第三定律可知汽车对桥的压力N = N（２）汽车的速度越大，汽车对桥的压力越小
汽车开始做平抛运动．
（３）当汽车的速度增大到 时,压力为零
1、汽车过凸形桥
问题2：质量为m的汽车以速度v通过半径为R的凹型桥。它经桥的最低点时对桥的压力为多大？比汽车的重量大还是小？速度越大压力越大还是越小？
N
G
【解】G和N的合力提供汽车做圆周运动的向心力，由牛顿第二定律得：
（２）可见汽车的速度越大对桥的压力越大。
（ 1 ）由牛顿第三定律可知汽车对桥的压力N = N>G
2、汽车过凹形桥
练习：一辆汽车匀速率通过半径为R的圆弧拱形路面，关于汽车的受力情况，下列说法正确的是（ ）
A．汽车对路面的压力大小不变，总是等于汽车的重力
B．汽车对路面的压力大小不断发生变化，总是小于汽车所受重力
C．汽车的牵引力大小不发生变化
D．汽车的牵引力大小逐渐变小
BD
3. 绳(外轨)
mg
T
解:
在最高点:　 T+ mg = mV2/R
解得:　 T = mV2/R- mg
依据此公式，你能找出T与V存在哪些关系？
1).小球对绳的拉力随速度的增大而增大；
　2).当 　　 时，T＝0, 小球恰过最高点;
　　　当Ｖ＞ 时，T>0;
　　　当Ｖ < 时，小球不能到达顶点.
4.杆(有内外轨)
问题: 质量为m的小球,套在长为L轻杆上在竖直平面内转动,在最高点, 试讨论小球的速度在什么范围内,杆对小球有支持力 在什么范围内,杆对小球有向下的拉力 速度为何值时,杆对小球无作用力
解:
(1).杆对小球有支持力N,
mg -N = mV2/R 所以 N = mg - mV2/R
根据题意, N>0,
　(3). 当　　　 时，N＝0, 杆对小球无作用力.
代入上式, V<
(2).杆对小球有拉力T,
mg +N = mV2/R 所以 N = mV2/R - mg
根据题意, T>0,代入上式, V>
T
mg
N
mg
问题: 质量为m的光滑小球,在半径为R的圆管内滚动,请讨论小球的速度在什么范围内,轨道内侧对小球有支持力 在什么范围内,轨道外侧对小球有向下的压力 速度为何值时,轨道与小球间无相互作用力
解:
(1). 轨道内侧对小球有支持力N,
mg -N = mV2/R 所以 N = mg - mV2/R
根据题意, N>0,
　(3). 当　　　 时，N＝0, 小球与轨道内侧外侧均无作用力.
N
mg
代入上式, V<
(2).轨道外侧对小球有压力N,
mg +N = mV2/R 所以 N = mV2/R - mg
N
mg
根据题意, N>0,代入上式, V>
5.有内外轨
凸桥(外轨)
轻绳(内轨)
轻杆(圆管)
最高点受力特点
产生背离圆心的力(支持力)
产生指向圆心的力(拉力或压力)
既可产生背离指向圆心的力也可产生指向圆心的力(支持力或拉力)
最高点特征方程
Mg+T = mV2/R
产生支持力:
mg- N = mV2/R
产生拉力:
做完整圆运动的条件
竖直平面内圆周运动几种模型比较
过山车、飞机在竖直平面翻筋斗、水流星与绳模型类似
mg- N = mV2/R
Mg+T = mV2/R
1﹑链球开始做什么运动？
2﹑链球离开运动员手以后做什么运动？
2008年北京奥运会期望我国的著名女链球运动员顾原在奥运动争取佳绩。链球的运动情况。
四.离心运动
1.离心运动定义：做匀速圆周运动的物体，在所受合力突然消失，或者不足以提供圆周运动所需的向心力的情况下，就做逐渐远离圆心的运动。这种运动叫做离心运动。
2.离心运动的条件：做匀速圆周运动的物体合外力消失或不足以提供所需的向心力
3.离心运动分析
当F=mω2r时，
物体做匀速圆周运动；
当F= 0时，
物体沿切线方向飞出；
当F＜mω2r时，
物体逐渐远离圆心；
当F＞mω2r时，
物体逐渐靠近圆心.
4.离心运动本质：
离心现象的本质是物体惯性的表现；
离心运动是物体逐渐远离圆心的一种物理现象。
5.离心运动的特点 ：
做圆周运动的质点，当合外力消失时，它就以这一时刻的线速度沿切线方向飞去．
做离心运动的质点是做半径越来越大的运动或沿切线方向飞出的运动，它不是沿半径方向飞出．
做离心运动的质点不存在所谓的“离心力”作用，因为没有任何物体提供这种力 ．
离心运动的应用
1、离心干燥器的金属网笼
利用离心运动把附着在物体上的水分甩掉的装置
解释：
o
F2
F
ν
当网笼转得比较慢时，水滴跟物体的附着力F 足以提供所需的向心力F 使水滴做圆周运动。当网笼转得比较快时，附着力 F 不足以提供所需的向心力 F，于是水滴做离心运动，穿过网孔，飞到网笼外面。
2、洗衣机的脱水筒
3、用离心机把体温计的水银柱甩回玻璃泡内
当离心机转得比较慢时，缩口的阻力 F 足以提供所需的向心力，缩口上方的水银柱做圆周运动。当离心机转得相当快时，阻力 F 不足以提供所需的向心力，水银柱做离心运动而进入玻璃泡内。
4、制作“棉花”糖的原理：
内筒与洗衣机的脱水筒相似，里面加入白砂糖，加热使糖熔化成糖汁。内筒高速旋转，黏稠的糖汁就做离心运动，从内筒壁的小孔飞散出去，成为丝状到达温度较低的外筒，并迅速冷却凝固，变得纤细雪白，像一团团棉花。
要使原来作圆周运动的物体作离心运动，该怎么办？
问题1：
A、提高转速，使所需向心力增大到大于物体所受合外力。
B、减小合外力或使其消失
离心运动的防止：
1、在水平公路上行驶的汽车转弯时
υ
F < m
υ
r
2
F
汽车
在水平公路上行驶的汽车，转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大，所需向心力F大于最大静摩擦力Fmax，汽车将做离心运动而造成交通事故。因此，在公路弯道处，车辆行驶不允许超过规定的速度。
2、高速转动的砂轮、飞轮等
问题2：
要防止离心现象发生，该怎么办？
A、减小物体运动的速度，使物体作圆周运动时所需的向心力减小
B、增大合外力，使其达到物体作圆周运动时所需的向心力
1、下列说法正确的是 ( )
A、作匀速圆周运动的物体，在所受合外力突然消失时，将沿圆周半径方向离开圆心；
B、作匀速圆周运动的物体，在所受合外力突然消失时，将沿圆周切线方向离开圆心；
C、作匀速圆周运动的物体，它自己会产生一个向心力，维持其作圆周运动；
D、作离心运动的物体，是因为受到离心力作用的缘故。
五.巩固练习：
B
２、为了防止汽车在水平路面上转弯时出现“打滑”的现象，可以：( )
A、增大汽车转弯时的速度　
B、减小汽车转弯时的速度
C、增大汽车与路面间的摩擦
D、减小汽车与路面间的摩擦
BC
3、物体做离心运动时，运动轨迹是（ ）
A．一定是直线。
B．一定是曲线。
C．可能是直线，也可能是曲线。
D．可能是圆。
C
4、下列说法中错误的有：（ ）
A、提高洗衣机脱水筒的转速，可以使衣服甩得更干
B、转动带有雨水的雨伞，水滴将沿圆周半径方向离开圆心
C、为了防止发生事故，高速转动的砂轮、飞轮等不能超过允许的最大转速
D、离心水泵利用了离心运动的原理
B
5、雨伞半径为R，高出地面h，雨伞以角速度ω旋转时，雨滴从伞边缘飞出（ ）
A．沿飞出点半径方向飞出，做平抛运动。
B．沿飞出点切线方向飞出，做平抛运动。
C．雨滴落在地面上后形成一个和伞半径相同的圆圈。
D．雨滴落在地面上形成一个半径　　　
的圆圈
6、质量为m物体A用线通过光滑的水平板上的小孔与质量为M砝码B相连，并且正在做匀速圆周运动，如图所示．如果减小M的质量，则物体的轨道半径r，角速度ω线速度v的大小变化情况是( )
A．r不变，v变小，ω变小
B．r增大，ω减小，v不变
C．r减小，v不变，ω增大
D．r减小，ω不变，v变小　　
1、明确对象，找出圆周平面，确定圆心及半径；
2、进行受力分析，画出受力图；
3、分析哪些力提供了向心力，并写出向心力的表达式；
4、根据向心力公式列方程求解。
六.能力提升
1：如图一圆盘可以绕一个通过圆盘中心且垂直于盘面的竖直轴转动，在圆盘上放置一木块，Z质量为1kg,动摩擦因数为0.4, 匀速转动的半径为1m,问若使得木块与圆盘不发生相对滑动,则转动的角速度不的超过多少
水平面
，三物体与转盘的摩擦力因数相同，三物体随转盘一起做匀速圆周运动，当转盘的转速逐渐增加时，以下说法正确的是（ ）
A. 物体A先滑动
B. 物体B先滑动
C. 物体C先滑动
D. 物体B、C同时先滑动
2：如图,已知物体A、B、C与转轴的距离为
，质量为
3： A、B两小球质量均为m,由轻杆相连,O为固定轴,AO=L,BO=2L,从图示位置释放,当B转至O点正下方,速度为多少 对轻杆的拉力为多少
A
B
O
4：物体m用线通过光滑的水平板间的小孔与砝码M相连,并且正在做匀速圆周运动,如果减小M的质量,则物体m的轨道半径R,角速度ω,线速度v应该怎么变化
5：如图,细绳的异端系着质量M=0.6kg的物体,静止在水平面上,另一端通过光滑小孔吊着质量m=3kg的物体,M的中点与原空的距离为0.2m,已知M和平面的最大静摩擦力为2N,现使的此平面绕中心轴线转动,问角速度在什么范围m会相对水平面静止
6：半径为Ｒ的圆周绕竖直中心轴oo 转动，小物体Ａ靠在圆筒的内壁上，他与圆筒的动摩擦因数为μ．现要使Ａ不下落，则圆筒转动的角速度ω至少要多少？
Ｏ
ω
Ｏ'
7、有一水平放置的圆盘，
上面放一劲度系数为K的弹簧，
弹簧的一端固定于转轴O上，
另一端拴一质量为m的物体A，
物体与盘面间的动摩擦因数为 。
开始物体A与圆盘一起转动时，弹簧
未发生形变，此时A离盘心O的距离为R。求:
A
O
盘转动的频率f达到多大时，物体A开始动？
当盘转动的频率达到2f时，弹簧的伸长量 x是多大？
8、如图所示，小球用轻绳通过桌面上一光滑小孔与物体B和C相连，小球能在光滑的水平桌面上做匀速圆周运动，若剪断B、C之间的细绳，当A球重新达到稳定状态后，则A球的( )
A.运动半径变大
B.速率变大
C.角速度变大
D.周期变大
P
Q
O
O
9：固定的光滑圆锥漏斗内壁,有两个质量相同的小球P和Q,分别紧贴着漏斗在水平面内做相同转向的匀速圆周运动,则（ ）
ACD
A.vP>vQ
B. vPC. aP=aQ
D. ωP<ωQ
10.在固定在地面的内壁光滑的半球形小碗中,两小球A和B在水平面内做匀速圆周运动,则（ ）
A.向心加速度aA>aB
B.对碗压力FA> FB
C.线速度vA>vB
D.周期TA>TB
A
B
AC
11、绳系着装水的桶，在竖直平面内做圆周运动，水的质量m=0.5kg，绳长=40cm.求
（1）桶在最高点水不流出的最小速率？（2）水在最高点速率=3m/s时水对桶底的压力？(g取10m/s2)
竖直面
12：线球模型,球质量m，绳长L.问给小球多大的Vo才能使小球在竖直面内做完整的圆周运动 试证明只要小求能做完整的圆周运动,则小球在最地点受到的拉力与小球在最高点手到的拉力之差为一恒定的值6mg.
Vo
13：如图所示，一质量为m的小球，放在一个内壁光滑的封闭管内，使其在竖直面内作圆周运动.(1)若过小球恰好能通过最高点，则小球在最高点和最低点的速度分别是多少？小球的受力情况分别如何？(2)若小球在最低点受到管道的力为6mg，则小球在最高点的速度及受到管道的力是多少？
mg
O
N
14：绳子系着装有水的木桶，在竖直面内做圆周运动，水的质量m=0.5kg，绳子长度为l=60cm，求：
A、最高点水不留出的最小速度？
B、设水在最高点速度为V=3m/s，求水对桶底的压力？
15：如图所示，一质量为m的小球，用长为L细绳系住，使其在竖直面内作圆周运动.(1)若过小球恰好能通过最高点，则小球在最高点和最低点的速度分别是多少？小球的受力情况分别如何？(2)若小球在最低点受到绳子的拉力为10mg，则小球在最高点的速度及受到绳子的拉力是多少？
mg
O
16:如图中圆弧轨道AB是在竖直平面内的1/4圆周，在B点，轨道的切线是水平的.一质点自A点从静止开始下滑，不计滑块与轨道间的摩擦和空气阻力，则在质点刚要到达B点时的加速度大小为______，刚滑过B点时的加速度大小为_____.
A
B
17、如图所示，质量为m的小球，用长为L的细绳，悬于光滑斜面上的o点，小球在这个倾角为θ的光滑斜面上做圆周运动，若小球在最高点和最低点的速率分别是vl和v2，则绳在这两个位置时的张力大小分别是多大
18：游乐场的过山车可以底朝上在圆轨道
上运行，游客却掉不下来，我们把这重情况
抽象为如图这种模型，弧形轨道的下端与竖直
圆轨道相连，使小球从弧形轨道上段滑下，
小球进入圆轨道下端后沿圆轨道运动，问小球
从离地面多高处释放，即可使小球刚好能做
完整的圆周运动？
h