5.3.2 函数的最值 第2课时 课件(共33张PPT)
文档属性
| 名称 | 5.3.2 函数的最值 第2课时 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 744.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 10:42:40 | ||
图片预览











文档简介
(共33张PPT)
第2课时 函数的最值
一、函数f(x)在区间[a,b]上的最值
【问题思考】
1.如图,观察函数y=f(x)在区间[a,b]上的图象,你能找出f(x)在区间[a,b]上的最大值与最小值吗
提示:能,函数y=f(x)在区间[a,b]上的最小值是f(x3),最大值是f(b).
2.填空:一般地,如果在区间[a,b]上函数y=f(x)的图象是一条 的曲线,那么它必有最大值和最小值.
连续不断
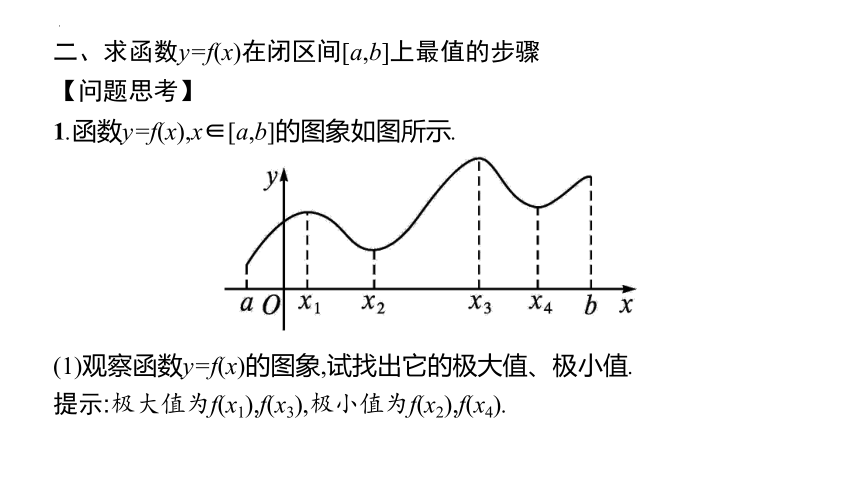
二、求函数y=f(x)在闭区间[a,b]上最值的步骤
【问题思考】
1.函数y=f(x),x∈[a,b]的图象如图所示.
(1)观察函数y=f(x)的图象,试找出它的极大值、极小值.
提示:极大值为f(x1),f(x3),极小值为f(x2),f(x4).
(2)结合图象判断函数y=f(x)在区间[a,b]上是否存在最大值、最小值 若存在,分别是多少
提示:存在,函数y=f(x)在区间[a,b]上的最小值是f(a),最大值是f(x3).
(3)函数y=f(x)在区间[a,b]上的最大值或最小值一定是某极值吗
提示:不一定,也可能是区间端点的函数值.
(4)怎样确定函数f(x)在区间[a,b]上的最小值和最大值
提示:比较极值与区间端点的函数值,最大的是最大值,最小的是最小值.
2.填空:
求函数y=f(x)在区间[a,b]上的最大值与最小值的步骤:
(1)求函数y=f(x)在区间(a,b)上的;
(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是, 最小的一个是.
3.想一想:如果函数y=f(x)在开区间(a,b)上只有一个极值,且为极小值,那么函数在开区间(a,b)上有最值吗
提示:有最小值,无最大值.设x0是函数的极小值点,则函数f(x)在区间(a,x0)上单调递减,在区间(x0,b)上单调递增,故函数f(x)在x0处取得最小值.
极值
最大值
最小值
4.做一做:函数y=2x3-3x2-12x+5在区间[-2,1]上的最大值、最小值分别是
( )
A.12,-8 B.1,-8
C.12,-15 D.5,-16
解析:y'=6x2-6x-12,
令y'=0,解得x=-1或x=2(舍去).
当x=-2时,y=1;当x=-1时,y=12;
当x=1时,y=-8,所以ymax=12,ymin=-8.故选A.
答案:A
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)闭区间上的函数一定有最值.( )
(2)函数的极值只能在区间内取得,而函数的最值可以在区间端点处取得.( )
(3)函数的最大值一定是极大值,函数的最小值也一定是极小值.( )
×
√
×
探究一
求函数在闭区间上的最值
【例1】 求函数f(x)=-x4+2x2+3在区间[-3,2]上的最大值与最小值.
解:因为f(x)=-x4+2x2+3,
所以f'(x)=-4x3+4x.
令f'(x)=-4x(x+1)(x-1)=0,解得x=-1或x=0或x=1.
在区间[-3,2]上,当x变化时,f'(x),f(x)的变化情况如下表所示.
x -3 (-3,-1) -1 (-1,0) 0 (0,1) 1 (1,2) 2
f'(x) + 0 - 0 + 0 -
f(x) -60 单调 递增 极大 值4 单调 递减 极小 值3 单调 递增 极大 值4 单调 递减 -5
所以,函数f(x)在区间[-3,2]上的最大值是4,最小值是-60.
把本例中“区间[-3,2]”改为“区间[0,2]”求相应问题.
解:令f'(x)=0,解得x=-1(舍去)或x=0或x=1.
在区间[0,2]上,当x变化时,f'(x),f(x)的变化情况如下表所示.
x 0 (0,1) 1 (1,2) 2
f'(x) + 0 -
f(x) 3 单调递增 极大值4 单调递减 -5
所以函数f(x)在区间[0,2]上的最大值是4,最小值是-5.
反思感悟 求解函数在固定区间上的最值,需注意以下几点:
(1)对函数进行准确求导,并检验f'(x)=0的根是否在给定区间内;
(2)研究函数的单调性,正确确定函数的极值和端点函数值;
(3)比较函数的极值与端点函数值大小,确定最值.
【变式训练1】 求函数f(x)=e-x-ex在区间[0,a]上的最大值与最小值,其中a>0,且为常数.
当x∈[0,a]时,f'(x)<0恒成立,
则函数f(x)在区间[0,a]上单调递减.
故当x=a时,f(x)有最小值f(a)=e-a-ea.
当x=0时,f(x)有最大值f(0)=0.
探究二
含参数的函数的求最值问题
【例2】 已知函数f(x)=(x-k)ex,k为常数.
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
解:(1)函数f(x)的定义域为R.
由f(x)=(x-k)ex,得f'(x)=(x-k+1)ex.
令f'(x)=0,解得x=k-1.
当x变化时,f(x)与f'(x)的
变化情况如下表:
所以函数f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).
x (-∞,k-1) k-1 (k-1,+∞)
f'(x) - 0 +
f(x) 单调递减 -ek-1 单调递增
(2)当k-1≤0,即k≤1时,函数f(x)在区间[0,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=-k;
当0当k-1≥1,即k≥2时,函数f(x)在区间[0,1]上单调递减,所以函数f(x)在区间[0,1]上的最小值为f(1)=(1-k)e.
综上可知,当k≤1时,f(x)min=f(0)=-k;
当1当k≥2时,f(x)min=f(1)=(1-k)e.
反思感悟 求函数f(x)在闭区间[a,b]上的最值的思路
判断函数在区间[a,b]上的单调性,若函数在区间[a,b]上单调递增或单调递减,则f(a),f(b)一个为最大值,一个为最小值.若函数在区间[a,b]上不单调,一般先求f(x)在区间[a,b]上的极值,再与f(a),f(b)比较,最大的即为最大值,最小的即为最小值.
探究三
由函数的最值求参数的值或取值范围
【例3】 已知函数f(x)=ax3-6ax2+b,问是否存在实数a,b,使f(x)在区间[-1,2]上取得最大值3,最小值-29 若存在,求出a,b的值;若不存在,请说明理由.
解:存在.显然a≠0,f'(x)=3ax2-12ax=3ax(x-4).
令f'(x)=0,解得x=0或x=4(舍去).
若a>0,在区间[-1,2]上当x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,函数f(x)取得最大值3,
即f(0)=b=3.
又因为f(2)=-16a+3,f(-1)=-7a+3,
所以f(-1)>f(2),
所以当x=2时,函数f(x)取得最小值-29,
即f(2)=-16a+3=-29,解得a=2.
若a<0,在区间[-1,2]上当x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,函数f(x)取得最小值-29,
即f(0)=b=-29.
又因为f(2)=-16a-29,f(-1)=-7a-29,
所以f(2)>f(-1).
所以当x=2时,函数f(x)取得最大值3,
即f(2)=-16a-29=3,解得a=-2.
综上所述,a=2,b=3或a=-2,b=-29.
反思感悟 已知函数的最值求参数值(取值范围)的思路
已知函数在某区间上的最值求参数的值是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.
【变式训练3】 已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(1)∵f'(x)=-3x2+6x+9.
令f'(x)<0,解得x<-1或x>3.
∴函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)∵f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,∴f(2)>f(-2).
由(1)知f'(x)=-3x2+6x+9,令f'(x)=0,
解得x=-1或x=3(舍去).
∵当x∈[-2,-1)时,f'(x)<0,
∴函数f(x)在区间[-2,-1)上单调递减.
又当x∈(-1,2]时,f'(x)>0,
∴函数f(x)在区间(-1,2]上单调递增.
∴f(2)和f(-1)分别是函数f(x)在区间[-2,2]上的最大值和最小值.
于是f(2)=22+a=20,解得a=-2.
∴f(x)=-x3+3x2+9x-2.
∴f(-1)=1+3-9-2=-7,即函数f(x)在区间[-2,2]上的最小值为-7.
求最值时忽视“端点值”而致错
【典例】 已知函数f(x)=(x2+1)(x+a)(a∈R),且f'(-1)=0,则函数y=f(x)在区间 上的最大值为 ,最小值为 .
错解:f(x)=x3+ax2+x+a,f'(x)=3x2+2ax+1.
f'(-1)=3-2a+1=0,解得a=2.
以上解答过程中都有哪些错误 出错的原因是什么 你如何改正 你如何防范
正解:f(x)=x3+ax2+x+a,f'(x)=3x2+2ax+1.
f'(-1)=3-2a+1=0,可得a=2.
防范措施 求函数的最值时,若函数的定义域是闭区间,则需比较极值点处的函数值与端点处的函数值的大小;如本例中需比较极值与端点处函数值的大小才能确定出最值.若函数的定义域是开区间,且只有一个极值点,则该极值点就是最值点.
【变式训练】 函数y=x+2cos x在区间 上取得最大值时,x的值为
( )
答案:B
解析:函数y的定义域为(0,+∞).
当x∈(0,e)时,y'>0,则函数y在区间(0,e)上单调递增;
当x∈(e,+∞)时,y'<0,则函数y在区间(e,+∞)上单调递减.
所以,当x=e时,函数y取得极大值也是最大值 ,故选A.
答案:A
2.若函数f(x)=x3-x2-x+a在区间[0,2]上的最大值是3,则a等于( )
A.3 B.1
C.2 D.-1
解析:f'(x)=3x2-2x-1,令f'(x)=0,
解得x=- (舍去)或x=1.
因为f(0)=a,f(1)=a-1,f(2)=a+2,
所以f(2)最大,即a+2=3,解得a=1.
答案:B
3.已知f(x)=-x2+mx+1在区间[-2,-1]上的最大值就是函数f(x)的极大值,则m的取值范围是 .
答案:(-4,-2)
4.已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m∈[-1,1],则f(m)的最小值为 .
解析:f'(x)=-3x2+2ax.
由函数f(x)在x=2处取得极值知f'(2)=0,
即-3×4+2a×2=0,解得a=3.
故f(x)=-x3+3x2-4,f'(x)=-3x2+6x.
f'(0)=0,且函数f(x)在区间(-1,0)上单调递减,在区间(0,1)上单调递增,
所以当m∈[-1,1]时,f(m)min=f(0)=-4.
答案:-4
5.已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.求a的值.
解:函数f(x)的定义域为(-a,+∞).
令f'(x)=0,解得x=1-a>-a.
当-a当x>1-a时,f'(x)>0,函数f(x)在区间(1-a,+∞)上单调递增.
因此函数f(x)在x=1-a处取得极小值,也是最小值.
由题意知f(1-a)=1-a=0,故a=1.
第2课时 函数的最值
一、函数f(x)在区间[a,b]上的最值
【问题思考】
1.如图,观察函数y=f(x)在区间[a,b]上的图象,你能找出f(x)在区间[a,b]上的最大值与最小值吗
提示:能,函数y=f(x)在区间[a,b]上的最小值是f(x3),最大值是f(b).
2.填空:一般地,如果在区间[a,b]上函数y=f(x)的图象是一条 的曲线,那么它必有最大值和最小值.
连续不断
二、求函数y=f(x)在闭区间[a,b]上最值的步骤
【问题思考】
1.函数y=f(x),x∈[a,b]的图象如图所示.
(1)观察函数y=f(x)的图象,试找出它的极大值、极小值.
提示:极大值为f(x1),f(x3),极小值为f(x2),f(x4).
(2)结合图象判断函数y=f(x)在区间[a,b]上是否存在最大值、最小值 若存在,分别是多少
提示:存在,函数y=f(x)在区间[a,b]上的最小值是f(a),最大值是f(x3).
(3)函数y=f(x)在区间[a,b]上的最大值或最小值一定是某极值吗
提示:不一定,也可能是区间端点的函数值.
(4)怎样确定函数f(x)在区间[a,b]上的最小值和最大值
提示:比较极值与区间端点的函数值,最大的是最大值,最小的是最小值.
2.填空:
求函数y=f(x)在区间[a,b]上的最大值与最小值的步骤:
(1)求函数y=f(x)在区间(a,b)上的;
(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是, 最小的一个是.
3.想一想:如果函数y=f(x)在开区间(a,b)上只有一个极值,且为极小值,那么函数在开区间(a,b)上有最值吗
提示:有最小值,无最大值.设x0是函数的极小值点,则函数f(x)在区间(a,x0)上单调递减,在区间(x0,b)上单调递增,故函数f(x)在x0处取得最小值.
极值
最大值
最小值
4.做一做:函数y=2x3-3x2-12x+5在区间[-2,1]上的最大值、最小值分别是
( )
A.12,-8 B.1,-8
C.12,-15 D.5,-16
解析:y'=6x2-6x-12,
令y'=0,解得x=-1或x=2(舍去).
当x=-2时,y=1;当x=-1时,y=12;
当x=1时,y=-8,所以ymax=12,ymin=-8.故选A.
答案:A
【思考辨析】
判断下列说法是否正确,正确的在后面的括号里画“√”,错误的画“×”.
(1)闭区间上的函数一定有最值.( )
(2)函数的极值只能在区间内取得,而函数的最值可以在区间端点处取得.( )
(3)函数的最大值一定是极大值,函数的最小值也一定是极小值.( )
×
√
×
探究一
求函数在闭区间上的最值
【例1】 求函数f(x)=-x4+2x2+3在区间[-3,2]上的最大值与最小值.
解:因为f(x)=-x4+2x2+3,
所以f'(x)=-4x3+4x.
令f'(x)=-4x(x+1)(x-1)=0,解得x=-1或x=0或x=1.
在区间[-3,2]上,当x变化时,f'(x),f(x)的变化情况如下表所示.
x -3 (-3,-1) -1 (-1,0) 0 (0,1) 1 (1,2) 2
f'(x) + 0 - 0 + 0 -
f(x) -60 单调 递增 极大 值4 单调 递减 极小 值3 单调 递增 极大 值4 单调 递减 -5
所以,函数f(x)在区间[-3,2]上的最大值是4,最小值是-60.
把本例中“区间[-3,2]”改为“区间[0,2]”求相应问题.
解:令f'(x)=0,解得x=-1(舍去)或x=0或x=1.
在区间[0,2]上,当x变化时,f'(x),f(x)的变化情况如下表所示.
x 0 (0,1) 1 (1,2) 2
f'(x) + 0 -
f(x) 3 单调递增 极大值4 单调递减 -5
所以函数f(x)在区间[0,2]上的最大值是4,最小值是-5.
反思感悟 求解函数在固定区间上的最值,需注意以下几点:
(1)对函数进行准确求导,并检验f'(x)=0的根是否在给定区间内;
(2)研究函数的单调性,正确确定函数的极值和端点函数值;
(3)比较函数的极值与端点函数值大小,确定最值.
【变式训练1】 求函数f(x)=e-x-ex在区间[0,a]上的最大值与最小值,其中a>0,且为常数.
当x∈[0,a]时,f'(x)<0恒成立,
则函数f(x)在区间[0,a]上单调递减.
故当x=a时,f(x)有最小值f(a)=e-a-ea.
当x=0时,f(x)有最大值f(0)=0.
探究二
含参数的函数的求最值问题
【例2】 已知函数f(x)=(x-k)ex,k为常数.
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
解:(1)函数f(x)的定义域为R.
由f(x)=(x-k)ex,得f'(x)=(x-k+1)ex.
令f'(x)=0,解得x=k-1.
当x变化时,f(x)与f'(x)的
变化情况如下表:
所以函数f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).
x (-∞,k-1) k-1 (k-1,+∞)
f'(x) - 0 +
f(x) 单调递减 -ek-1 单调递增
(2)当k-1≤0,即k≤1时,函数f(x)在区间[0,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=-k;
当0
综上可知,当k≤1时,f(x)min=f(0)=-k;
当1
反思感悟 求函数f(x)在闭区间[a,b]上的最值的思路
判断函数在区间[a,b]上的单调性,若函数在区间[a,b]上单调递增或单调递减,则f(a),f(b)一个为最大值,一个为最小值.若函数在区间[a,b]上不单调,一般先求f(x)在区间[a,b]上的极值,再与f(a),f(b)比较,最大的即为最大值,最小的即为最小值.
探究三
由函数的最值求参数的值或取值范围
【例3】 已知函数f(x)=ax3-6ax2+b,问是否存在实数a,b,使f(x)在区间[-1,2]上取得最大值3,最小值-29 若存在,求出a,b的值;若不存在,请说明理由.
解:存在.显然a≠0,f'(x)=3ax2-12ax=3ax(x-4).
令f'(x)=0,解得x=0或x=4(舍去).
若a>0,在区间[-1,2]上当x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,函数f(x)取得最大值3,
即f(0)=b=3.
又因为f(2)=-16a+3,f(-1)=-7a+3,
所以f(-1)>f(2),
所以当x=2时,函数f(x)取得最小值-29,
即f(2)=-16a+3=-29,解得a=2.
若a<0,在区间[-1,2]上当x变化时,f'(x),f(x)的变化情况如下表:
所以当x=0时,函数f(x)取得最小值-29,
即f(0)=b=-29.
又因为f(2)=-16a-29,f(-1)=-7a-29,
所以f(2)>f(-1).
所以当x=2时,函数f(x)取得最大值3,
即f(2)=-16a-29=3,解得a=-2.
综上所述,a=2,b=3或a=-2,b=-29.
反思感悟 已知函数的最值求参数值(取值范围)的思路
已知函数在某区间上的最值求参数的值是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.
【变式训练3】 已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(1)∵f'(x)=-3x2+6x+9.
令f'(x)<0,解得x<-1或x>3.
∴函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)∵f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,∴f(2)>f(-2).
由(1)知f'(x)=-3x2+6x+9,令f'(x)=0,
解得x=-1或x=3(舍去).
∵当x∈[-2,-1)时,f'(x)<0,
∴函数f(x)在区间[-2,-1)上单调递减.
又当x∈(-1,2]时,f'(x)>0,
∴函数f(x)在区间(-1,2]上单调递增.
∴f(2)和f(-1)分别是函数f(x)在区间[-2,2]上的最大值和最小值.
于是f(2)=22+a=20,解得a=-2.
∴f(x)=-x3+3x2+9x-2.
∴f(-1)=1+3-9-2=-7,即函数f(x)在区间[-2,2]上的最小值为-7.
求最值时忽视“端点值”而致错
【典例】 已知函数f(x)=(x2+1)(x+a)(a∈R),且f'(-1)=0,则函数y=f(x)在区间 上的最大值为 ,最小值为 .
错解:f(x)=x3+ax2+x+a,f'(x)=3x2+2ax+1.
f'(-1)=3-2a+1=0,解得a=2.
以上解答过程中都有哪些错误 出错的原因是什么 你如何改正 你如何防范
正解:f(x)=x3+ax2+x+a,f'(x)=3x2+2ax+1.
f'(-1)=3-2a+1=0,可得a=2.
防范措施 求函数的最值时,若函数的定义域是闭区间,则需比较极值点处的函数值与端点处的函数值的大小;如本例中需比较极值与端点处函数值的大小才能确定出最值.若函数的定义域是开区间,且只有一个极值点,则该极值点就是最值点.
【变式训练】 函数y=x+2cos x在区间 上取得最大值时,x的值为
( )
答案:B
解析:函数y的定义域为(0,+∞).
当x∈(0,e)时,y'>0,则函数y在区间(0,e)上单调递增;
当x∈(e,+∞)时,y'<0,则函数y在区间(e,+∞)上单调递减.
所以,当x=e时,函数y取得极大值也是最大值 ,故选A.
答案:A
2.若函数f(x)=x3-x2-x+a在区间[0,2]上的最大值是3,则a等于( )
A.3 B.1
C.2 D.-1
解析:f'(x)=3x2-2x-1,令f'(x)=0,
解得x=- (舍去)或x=1.
因为f(0)=a,f(1)=a-1,f(2)=a+2,
所以f(2)最大,即a+2=3,解得a=1.
答案:B
3.已知f(x)=-x2+mx+1在区间[-2,-1]上的最大值就是函数f(x)的极大值,则m的取值范围是 .
答案:(-4,-2)
4.已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m∈[-1,1],则f(m)的最小值为 .
解析:f'(x)=-3x2+2ax.
由函数f(x)在x=2处取得极值知f'(2)=0,
即-3×4+2a×2=0,解得a=3.
故f(x)=-x3+3x2-4,f'(x)=-3x2+6x.
f'(0)=0,且函数f(x)在区间(-1,0)上单调递减,在区间(0,1)上单调递增,
所以当m∈[-1,1]时,f(m)min=f(0)=-4.
答案:-4
5.已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.求a的值.
解:函数f(x)的定义域为(-a,+∞).
令f'(x)=0,解得x=1-a>-a.
当-a
因此函数f(x)在x=1-a处取得极小值,也是最小值.
由题意知f(1-a)=1-a=0,故a=1.
