苏教版六年级下册第六单元正比例和反比例总复习课件(共18张PPT)
文档属性
| 名称 | 苏教版六年级下册第六单元正比例和反比例总复习课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 18.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 17:07:52 | ||
图片预览



文档简介
(共18张PPT)
正比例和反比例总复习
苏教版六年级
下册
1.正比例、反比例的意义;
2.正比例、反比例的联系和区别;
3.是否成正比例或反比例的思考方法;
4.灵活应用,解决实际问题。
明确目标
复习意义
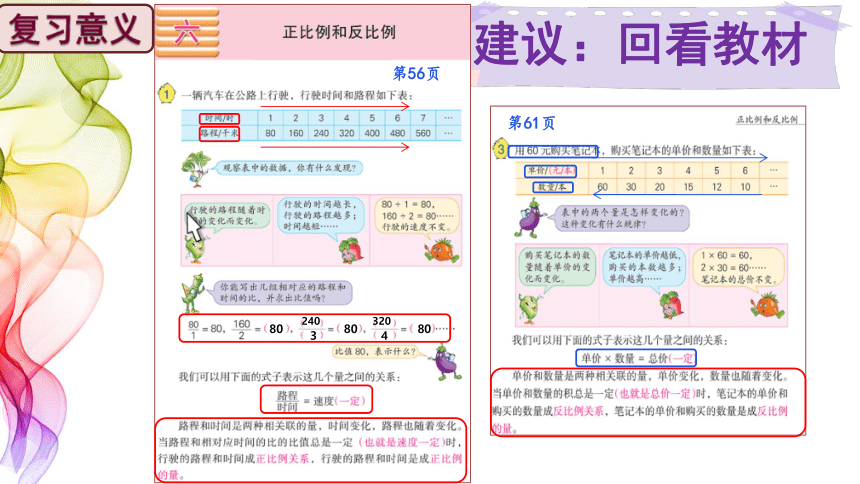
建议:回看教材
第61页
第56页
80
240
3
80
320
4
80
自主梳理
正比例 反比例
相同点 不 同 点 变化规律
运算
关系式
图像
都有两种相关联的量
(一种量随着另一种量的变化而变化)
两种量同时扩大或缩小
一种量扩大,另一种量缩小。
相对应的两个数的比值(商)一定
相对应的两个数的积一定
x × y =k(一定)
建议:比较异同
思考判断
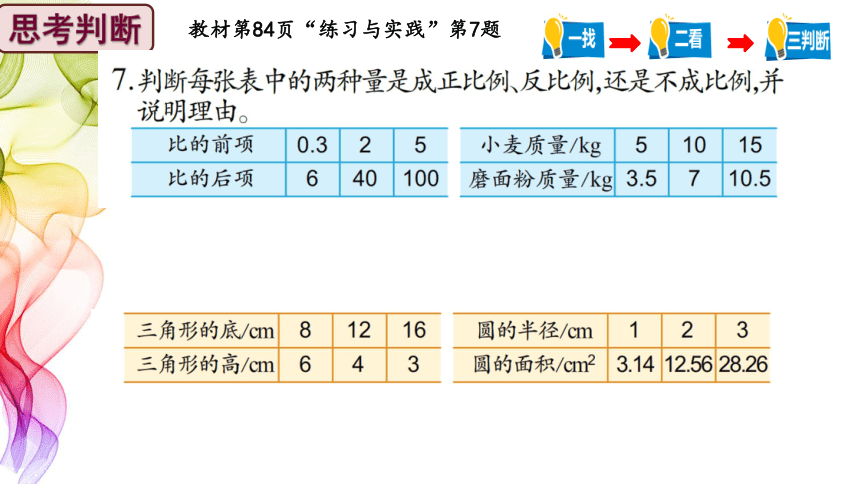
教材第84页“练习与实践”第7题
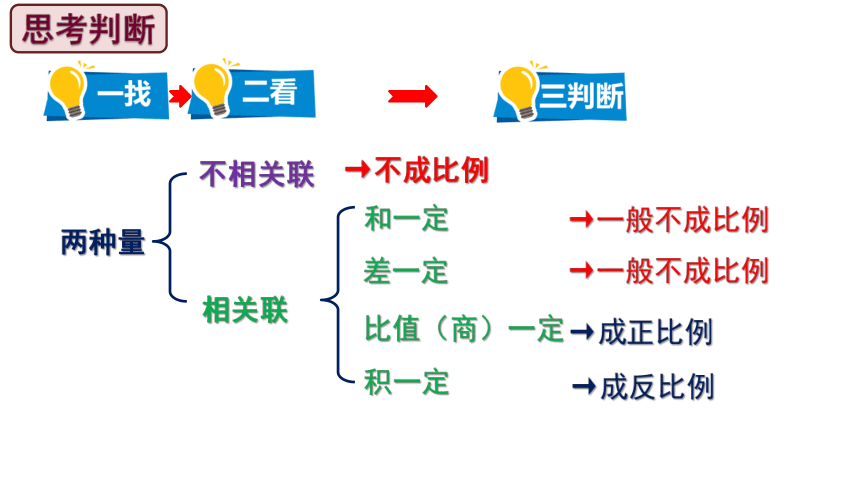
两种量
不相关联
相关联
和一定
差一定
比值(商)一定
积一定
→不成比例
→一般不成比例
→一般不成比例
→成反比例
→成正比例
思考判断
思考判断
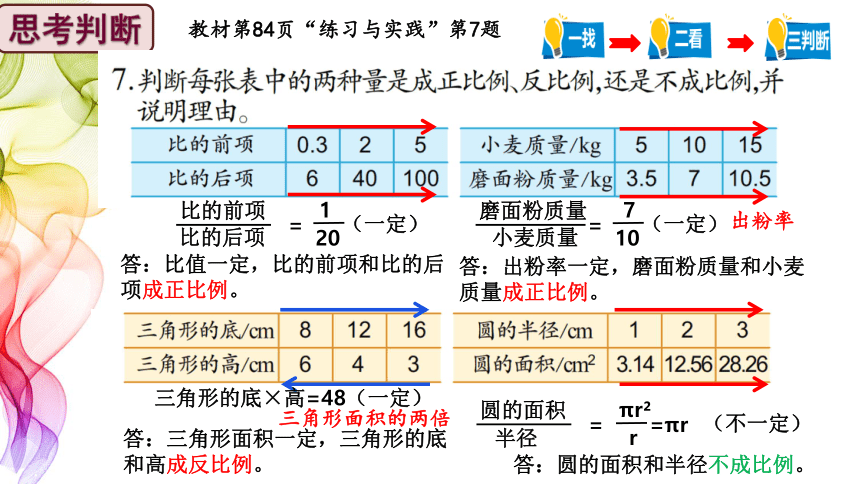
教材第84页“练习与实践”第7题
=
磨面粉质量
小麦质量
7
10
(一定)
=
比的前项
比的后项
1
20
(一定)
出粉率
答:比值一定,比的前项和比的后项成正比例。
答:出粉率一定,磨面粉质量和小麦质量成正比例。
三角形的底×高=48(一定)
三角形面积的两倍
答:三角形面积一定,三角形的底和高成反比例。
= =πr
圆的面积
半径
πr
r
(不一定)
答:圆的面积和半径不成比例。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
(1)步测一段距离,每步的平均长度和走的步数。
(2)一台压路机滚筒滚动的转数和压路的面积。
每步的平均长度×走的步数=步测的距离(一定)
答:步测距离一定,每步的平均长度和走的步数成反比例。
=
压路的面积
滚动的转数
(一定)
滚筒的侧面积
答:滚筒侧面积一定,压路的面积和滚动的转数成正比例。
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
答:收割效率一定,麦地面积和收割时间成正比例。
=
麦地面积
收割时间
(一定)
收割机每小时收割麦子的面积
答:每天借出本数和还回本数不相关联,所以不成比例。
(5)已知 x y = 10, x 和 y。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
(6补充)长方形周长一定,长和宽。
xy=10(一定)
答:积一定,x和y成反比例。
答:长方形周长一定,长和宽不成比例。
(长+宽)×2=长方形周长(一定)
长+宽=长方形周长的一半(一定)
(7补充)小红和爸爸的年龄.
爸爸年龄-小红年龄=年龄差(一定)
答:爸爸年龄和小红年龄不成比例。
建议:循序渐进
综合应用
教材第85页“练习与实践”第9题
路程/千米
耗油量/升
0
50
100
150
200
250
2
4
6
8
10
12
14
16
9. 右图表示一辆汽车在高速公路上
行驶的路程和耗油量的关系。
(1)这辆汽车在高速公路上行驶的路程和耗油量成正比例吗?为什么?
(2)根据图像判断,行驶75千米耗油多少升?
75
答:行驶75千米耗油6升。
综合应用
教材第84页“练习与实践”第9题
路程/千米
耗油量/升
0
50
100
150
200
250
2
4
6
8
10
12
14
16
9. 右图表示一辆汽车在高速公路上
行驶的路程和耗油量的关系。
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油量,在右图中描出行驶50千米、100 千米……路程和耗油量对应的点,再按顺序连接起来。
75
高速公路行驶
市区行驶
陡
建议:分析推理
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(1)你能通过在图中描
点连线,找出哪一
杯中纯酒精与蒸馏
水体积的比和其他
几杯不一样吗?
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(2)这一杯酒精溶液中纯
酒精与蒸馏水体积的
比是多少?纯酒精与
酒精溶液呢?
答:这一杯酒精溶液中纯
酒精与蒸馏水体积的
比是5︰2.
纯酒精与蒸馏水的混合物
纯酒精与酒精溶液的比是( ︰ ).
5
7
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(3)其他几杯酒精溶液中
纯酒精与酒精溶液体
积的比各是多少?
答:其他几杯酒精溶液中
纯酒精与酒精溶液体
积的比都是3︰4。
总结回顾
复习意义
自主梳理
思考判断
综合应用
小红看故事书,3天看了63页。照这样计算,7天可以看多少页?
学校要把一批树苗栽到科普基地,如果每行栽10棵,正好是18行;如果每行栽12棵,可以栽多少行?
每天看的页数一定,(看的页数)和(看的天数)成正比例。
树苗的总棵数一定,(每行栽的棵树)和(行数)成反比例。
实际问题中的正、反比例
解:设7天可以看x页。
63
3
=
x
7
解:设每行栽12棵,可以栽x行。
12x = 10×18
组成比例
列出方程
感谢观看!
正比例和反比例总复习
苏教版六年级
下册
1.正比例、反比例的意义;
2.正比例、反比例的联系和区别;
3.是否成正比例或反比例的思考方法;
4.灵活应用,解决实际问题。
明确目标
复习意义
建议:回看教材
第61页
第56页
80
240
3
80
320
4
80
自主梳理
正比例 反比例
相同点 不 同 点 变化规律
运算
关系式
图像
都有两种相关联的量
(一种量随着另一种量的变化而变化)
两种量同时扩大或缩小
一种量扩大,另一种量缩小。
相对应的两个数的比值(商)一定
相对应的两个数的积一定
x × y =k(一定)
建议:比较异同
思考判断
教材第84页“练习与实践”第7题
两种量
不相关联
相关联
和一定
差一定
比值(商)一定
积一定
→不成比例
→一般不成比例
→一般不成比例
→成反比例
→成正比例
思考判断
思考判断
教材第84页“练习与实践”第7题
=
磨面粉质量
小麦质量
7
10
(一定)
=
比的前项
比的后项
1
20
(一定)
出粉率
答:比值一定,比的前项和比的后项成正比例。
答:出粉率一定,磨面粉质量和小麦质量成正比例。
三角形的底×高=48(一定)
三角形面积的两倍
答:三角形面积一定,三角形的底和高成反比例。
= =πr
圆的面积
半径
πr
r
(不一定)
答:圆的面积和半径不成比例。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
(1)步测一段距离,每步的平均长度和走的步数。
(2)一台压路机滚筒滚动的转数和压路的面积。
每步的平均长度×走的步数=步测的距离(一定)
答:步测距离一定,每步的平均长度和走的步数成反比例。
=
压路的面积
滚动的转数
(一定)
滚筒的侧面积
答:滚筒侧面积一定,压路的面积和滚动的转数成正比例。
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
答:收割效率一定,麦地面积和收割时间成正比例。
=
麦地面积
收割时间
(一定)
收割机每小时收割麦子的面积
答:每天借出本数和还回本数不相关联,所以不成比例。
(5)已知 x y = 10, x 和 y。
思考判断
教材第85页“练习与实践”第8题
8. 判断各题的两种量是否成比例,成比例的是成正比例还是反比例?
(6补充)长方形周长一定,长和宽。
xy=10(一定)
答:积一定,x和y成反比例。
答:长方形周长一定,长和宽不成比例。
(长+宽)×2=长方形周长(一定)
长+宽=长方形周长的一半(一定)
(7补充)小红和爸爸的年龄.
爸爸年龄-小红年龄=年龄差(一定)
答:爸爸年龄和小红年龄不成比例。
建议:循序渐进
综合应用
教材第85页“练习与实践”第9题
路程/千米
耗油量/升
0
50
100
150
200
250
2
4
6
8
10
12
14
16
9. 右图表示一辆汽车在高速公路上
行驶的路程和耗油量的关系。
(1)这辆汽车在高速公路上行驶的路程和耗油量成正比例吗?为什么?
(2)根据图像判断,行驶75千米耗油多少升?
75
答:行驶75千米耗油6升。
综合应用
教材第84页“练习与实践”第9题
路程/千米
耗油量/升
0
50
100
150
200
250
2
4
6
8
10
12
14
16
9. 右图表示一辆汽车在高速公路上
行驶的路程和耗油量的关系。
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油量,在右图中描出行驶50千米、100 千米……路程和耗油量对应的点,再按顺序连接起来。
75
高速公路行驶
市区行驶
陡
建议:分析推理
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(1)你能通过在图中描
点连线,找出哪一
杯中纯酒精与蒸馏
水体积的比和其他
几杯不一样吗?
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(2)这一杯酒精溶液中纯
酒精与蒸馏水体积的
比是多少?纯酒精与
酒精溶液呢?
答:这一杯酒精溶液中纯
酒精与蒸馏水体积的
比是5︰2.
纯酒精与蒸馏水的混合物
纯酒精与酒精溶液的比是( ︰ ).
5
7
综合应用
教材第85页“练习与实践”第10题
10.纯酒精和蒸馏水可以配成酒精溶液。沈老师按表中的数据配制了4杯酒精溶液。
(3)其他几杯酒精溶液中
纯酒精与酒精溶液体
积的比各是多少?
答:其他几杯酒精溶液中
纯酒精与酒精溶液体
积的比都是3︰4。
总结回顾
复习意义
自主梳理
思考判断
综合应用
小红看故事书,3天看了63页。照这样计算,7天可以看多少页?
学校要把一批树苗栽到科普基地,如果每行栽10棵,正好是18行;如果每行栽12棵,可以栽多少行?
每天看的页数一定,(看的页数)和(看的天数)成正比例。
树苗的总棵数一定,(每行栽的棵树)和(行数)成反比例。
实际问题中的正、反比例
解:设7天可以看x页。
63
3
=
x
7
解:设每行栽12棵,可以栽x行。
12x = 10×18
组成比例
列出方程
感谢观看!
