梅州中学2020-2021高二下学期数学周练(8)(word版含答案)
文档属性
| 名称 | 梅州中学2020-2021高二下学期数学周练(8)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 20:36:13 | ||
图片预览

文档简介
高二数学第八周练习
一、选择题(每小题5分,共4小题20分)
1. 的展开式中的系数为( )
A. B.
C. D.
2. 某地区气象台统计,该地区下雨的概率是,刮风的概率为,既刮风又下雨的概率为,则在下雨天里,刮风的概率为( )
A. B. C. D.
3. 中为其内角,设,,且,则( )
A. B. C. D.
4. 复数,则的共轭复数的虚部为( )
A. B. C. D.
二、多选题(每小题4分,共1小题4分)
5. 有本不同的书,按下列方式进行分配,其中分配种数正确的是( )
A. 分给甲 乙 丙三人,每人各本,有种分法
B. 分给甲 乙 丙三人中,一人本,另两人各本,有种分法
C. 分给甲乙每人各本,分给丙丁每人各本,有种分法
D. 分给甲乙丙丁四人,有两人各本,另两人各本,有种分法
三、填空题(每小题5分,共2小题10分)
6. 某盏吊灯上并联着3个灯泡,如果在某段时间内每个灯泡能正常照明的概率都是,则在这段时间内吊灯能照明的概率是__________.
7. 已知正三棱锥所有棱长均为,且四个顶点都在同一个球面上,则该球的表面积为__________.
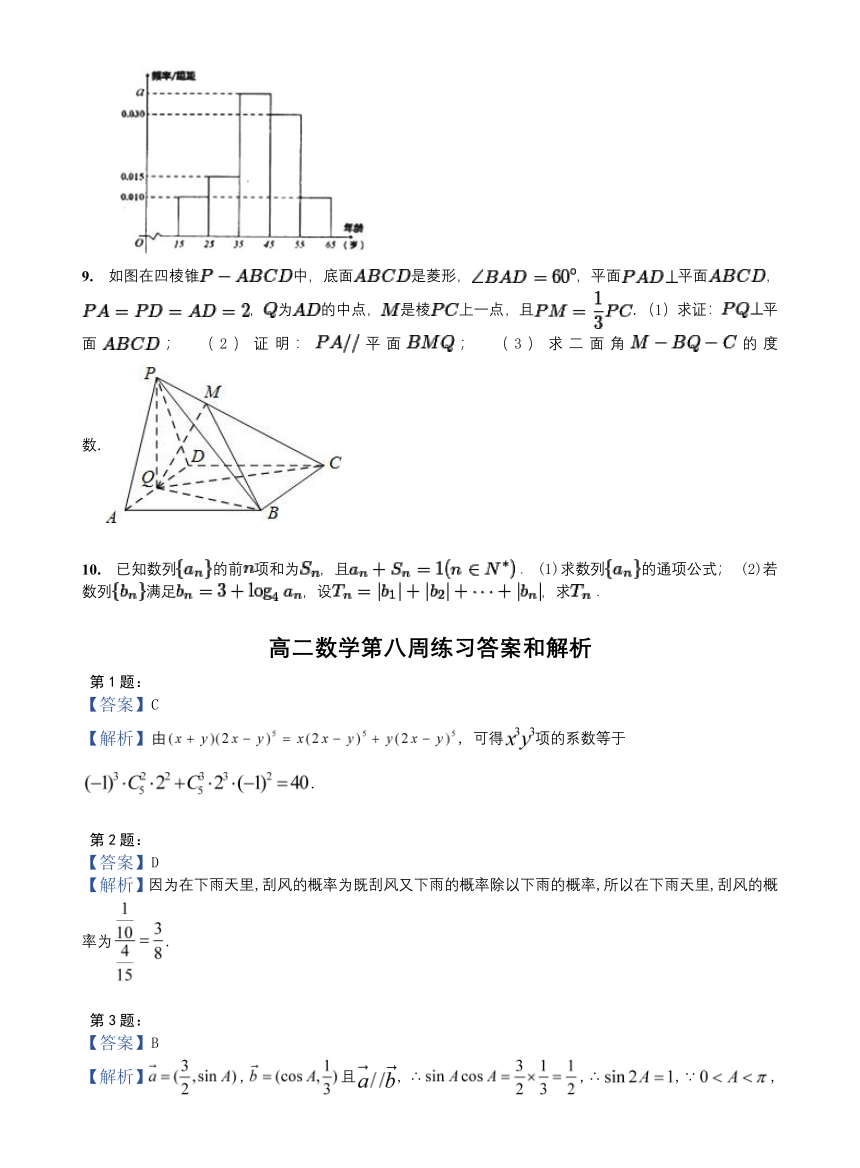
8. 树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占.现从参与调查人群中随机选出人,并将这人按年龄分组:第组,第组,第组,第组,第组得到频率分布直方图如图所示: (1)求的值; (2)现在要从年龄较小的第组中用分层抽样的方法抽取人,再从这人中随机抽取人进行问卷调查,求第组中抽到人的前提下,第组被抽到人的概率.
(3)若从所有参与调查的人中任意选出人,记关注“生态文明”的人数为,求的分布列.
9. 如图在四棱锥中,底面是菱形,,平面平面,,为的中点,是棱上一点,且.(1)求证:平面; (2)证明:平面; (3)求二面角的度数.
10. 已知数列的前项和为,且. (1)求数列的通项公式; (2)若数列满足,设,求.
高二数学第八周练习答案和解析
第1题:
【答案】C
【解析】由, 可得项的系数等于.
第2题:
【答案】D
【解析】因为在下雨天里,刮风的概率为既刮风又下雨的概率除以下雨的概率,所以在下雨天里,刮风的概率为.
第3题:
【答案】B
【解析】,且, ∴,∴,∵, 所以,∴,.故选:B.
第4题:
【答案】B
【解析】, ∴,虚部为.故选B.
第5题:
【答案】A,B,C
【解析】对A,先从本书中分给甲本,有种方法;再从其余的本书中分给乙本,有种方法;最后的本书给丙,有种方法,所以不同的分配方法有种,故A正确; 对B,先把本书分成堆:本、本、本,有种方法;再分给甲 乙 丙三人,所以不同的分配方法有种,故B正确; 对C,本不同的书先分给甲乙每人各本,有种方法;其余本分给丙丁,有种方法,所以不同的分配方法有种,故C正确; 对D,先把本不同的书分成堆:本、本、本、本,有种方法;再分给甲乙丙丁四人,所以不同的分配方法有种,故D错误.故选ABC.
第6题:
【答案】
【解析】依题意可知在某段时间内每个灯泡不能正常照明的概率都是,由于线路是并联电路,所以在这段时间内吊灯能照明的概率是.
第7题:
【答案】
【解析】构造一个各棱长为1的正方体,连接各面的对角线可作出一个正四面体, 此四面体各棱为, 而此四面体的外接球即为正方体的外接球. 此球的直径为正方体的对角线,即, 所以该球表面积. 故答案为:.
第8题:
【答案】见解析
【解析】(1)由,得. (2)第组的人数分别为人,人,人, 从第组中用分层抽样的方法抽取人, 则第组抽取的人数分别为人,人,人. 设从人中随机抽取人,第组已被抽到人为事件, 第组抽到人为事件,则. (3)从所有参与调查的人中任意选出人,关注“生态文明”的概率为,的可能取值为. ∴,. 所以的分布列为∵,.
第9题:
【答案】(1)略; (2)略; (3)
【解析】(1)由已知,为的中点,∴, 又∵平面平面,且平面平面,面, ∴平面. (2)连接,交于,连接, ∵底面是菱形,∴, ∴∽,,∴, 又,∴,∴, 又平面,平面, ∴平面.(3)连结,底面是菱形,且, ∴是等边三角形,∴, 由(1)平面.∴. 以为坐标原点,,,分别为轴,轴,轴建立空间直角坐标系, 则,,,. 设平面的法向量为, ∴注意到,∴解得是平面的一个法向量, 又平面的法向量为, 设二面角的大小为, ∴,∴, 即二面角二面角的度数为.
第10题:
【答案】(1); (2).
【解析】(1)∵, ∴,两式相减得.∴. ∴为公式为的等比数列. 又时,.∴,∴,∴的通项公式:. (2),∴,, ∴.
一、选择题(每小题5分,共4小题20分)
1. 的展开式中的系数为( )
A. B.
C. D.
2. 某地区气象台统计,该地区下雨的概率是,刮风的概率为,既刮风又下雨的概率为,则在下雨天里,刮风的概率为( )
A. B. C. D.
3. 中为其内角,设,,且,则( )
A. B. C. D.
4. 复数,则的共轭复数的虚部为( )
A. B. C. D.
二、多选题(每小题4分,共1小题4分)
5. 有本不同的书,按下列方式进行分配,其中分配种数正确的是( )
A. 分给甲 乙 丙三人,每人各本,有种分法
B. 分给甲 乙 丙三人中,一人本,另两人各本,有种分法
C. 分给甲乙每人各本,分给丙丁每人各本,有种分法
D. 分给甲乙丙丁四人,有两人各本,另两人各本,有种分法
三、填空题(每小题5分,共2小题10分)
6. 某盏吊灯上并联着3个灯泡,如果在某段时间内每个灯泡能正常照明的概率都是,则在这段时间内吊灯能照明的概率是__________.
7. 已知正三棱锥所有棱长均为,且四个顶点都在同一个球面上,则该球的表面积为__________.
8. 树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占.现从参与调查人群中随机选出人,并将这人按年龄分组:第组,第组,第组,第组,第组得到频率分布直方图如图所示: (1)求的值; (2)现在要从年龄较小的第组中用分层抽样的方法抽取人,再从这人中随机抽取人进行问卷调查,求第组中抽到人的前提下,第组被抽到人的概率.
(3)若从所有参与调查的人中任意选出人,记关注“生态文明”的人数为,求的分布列.
9. 如图在四棱锥中,底面是菱形,,平面平面,,为的中点,是棱上一点,且.(1)求证:平面; (2)证明:平面; (3)求二面角的度数.
10. 已知数列的前项和为,且. (1)求数列的通项公式; (2)若数列满足,设,求.
高二数学第八周练习答案和解析
第1题:
【答案】C
【解析】由, 可得项的系数等于.
第2题:
【答案】D
【解析】因为在下雨天里,刮风的概率为既刮风又下雨的概率除以下雨的概率,所以在下雨天里,刮风的概率为.
第3题:
【答案】B
【解析】,且, ∴,∴,∵, 所以,∴,.故选:B.
第4题:
【答案】B
【解析】, ∴,虚部为.故选B.
第5题:
【答案】A,B,C
【解析】对A,先从本书中分给甲本,有种方法;再从其余的本书中分给乙本,有种方法;最后的本书给丙,有种方法,所以不同的分配方法有种,故A正确; 对B,先把本书分成堆:本、本、本,有种方法;再分给甲 乙 丙三人,所以不同的分配方法有种,故B正确; 对C,本不同的书先分给甲乙每人各本,有种方法;其余本分给丙丁,有种方法,所以不同的分配方法有种,故C正确; 对D,先把本不同的书分成堆:本、本、本、本,有种方法;再分给甲乙丙丁四人,所以不同的分配方法有种,故D错误.故选ABC.
第6题:
【答案】
【解析】依题意可知在某段时间内每个灯泡不能正常照明的概率都是,由于线路是并联电路,所以在这段时间内吊灯能照明的概率是.
第7题:
【答案】
【解析】构造一个各棱长为1的正方体,连接各面的对角线可作出一个正四面体, 此四面体各棱为, 而此四面体的外接球即为正方体的外接球. 此球的直径为正方体的对角线,即, 所以该球表面积. 故答案为:.
第8题:
【答案】见解析
【解析】(1)由,得. (2)第组的人数分别为人,人,人, 从第组中用分层抽样的方法抽取人, 则第组抽取的人数分别为人,人,人. 设从人中随机抽取人,第组已被抽到人为事件, 第组抽到人为事件,则. (3)从所有参与调查的人中任意选出人,关注“生态文明”的概率为,的可能取值为. ∴,. 所以的分布列为∵,.
第9题:
【答案】(1)略; (2)略; (3)
【解析】(1)由已知,为的中点,∴, 又∵平面平面,且平面平面,面, ∴平面. (2)连接,交于,连接, ∵底面是菱形,∴, ∴∽,,∴, 又,∴,∴, 又平面,平面, ∴平面.(3)连结,底面是菱形,且, ∴是等边三角形,∴, 由(1)平面.∴. 以为坐标原点,,,分别为轴,轴,轴建立空间直角坐标系, 则,,,. 设平面的法向量为, ∴注意到,∴解得是平面的一个法向量, 又平面的法向量为, 设二面角的大小为, ∴,∴, 即二面角二面角的度数为.
第10题:
【答案】(1); (2).
【解析】(1)∵, ∴,两式相减得.∴. ∴为公式为的等比数列. 又时,.∴,∴,∴的通项公式:. (2),∴,, ∴.
同课章节目录
