北师大版六年数学下册总复习图形与测量(三)表格式教案
文档属性
| 名称 | 北师大版六年数学下册总复习图形与测量(三)表格式教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览


文档简介
课题 名称 北师大版六年数学下册总复习图形与测量(三)教案
教材内容 教材第96页内容。
目标 能正确计算常见立体图形的表面积和体积,并解决一些简单的实际问题。
重点 会正确计算立体图体的表面积与体积。
难点 提高学生解决问题的能力,发展学生的空间能力。
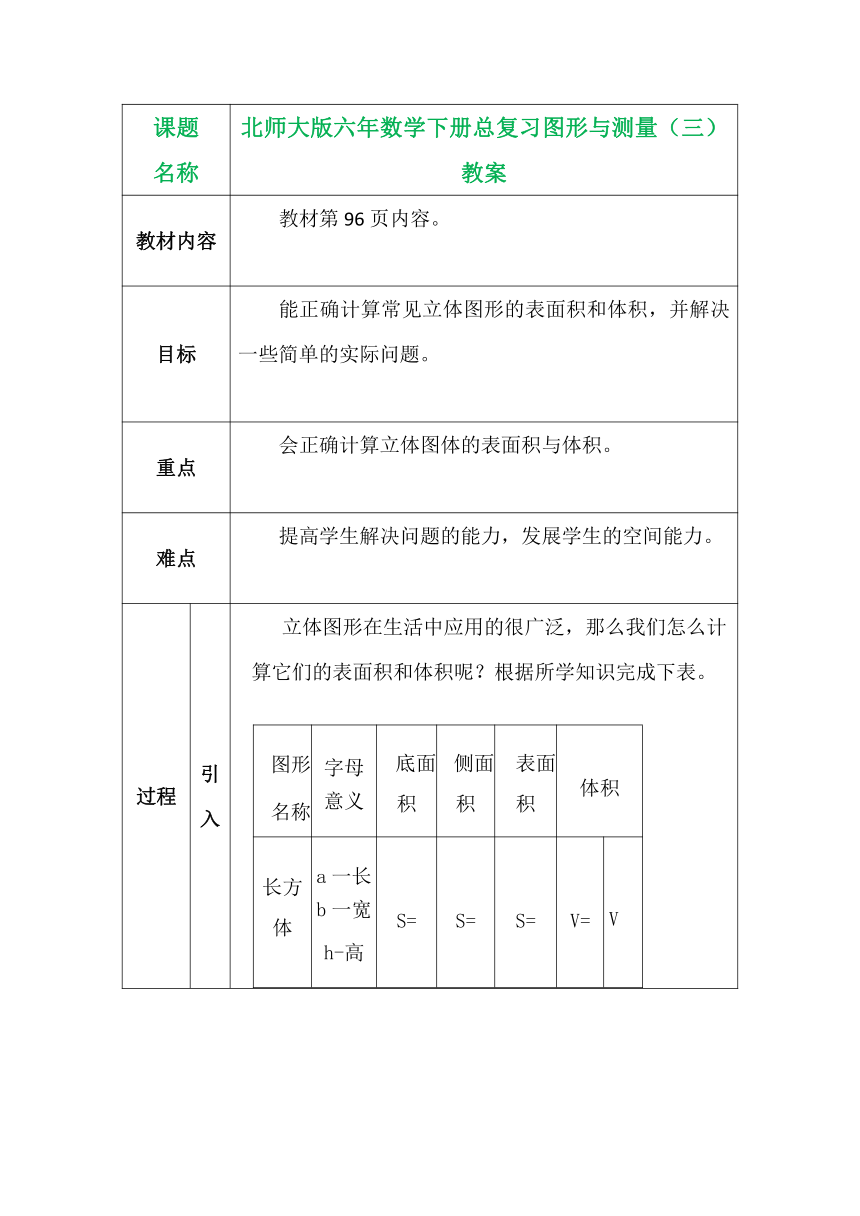
过程 引入 立体图形在生活中应用的很广泛,那么我们怎么计算它们的表面积和体积呢?根据所学知识完成下表。 图形名称字母 意义底面 积侧面 积表面 积体积长方 体a一长 b一宽 h-高S=S=S=V=V正方 体a一棱 长S=S=S=V=圆柱S-底 面积 r一底 面半径 h-高 C-底 面周长S=S=S==A圆锥S-底 面积 r一底 面半径 h-高S=S=S=V=
探新 1.在实际生活中立体图形的表面积应如何计算? 2.立体图形的容积和体积计算有什么区别与联系? 学生讨论,教师查看并做出一些指导。 汇报: 表面积:一个立体图形所有面的面积总和叫做它的表面积。 体积:一个立体图形所占空间的大小叫做它的体积。 应用中: 计算表面积要注意一共要算哪几个面的面积。 计算体积要弄清实际情况,计算容积要从容器里面量。
巩固 1. (1)如图,做两个无盖鱼缸,至少各需要多少平方厘米玻璃? (2)哪个鱼缸盛水多,先猜一猜,再计算多多少升? 2.要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸? 2. 1.把一个圆柱体沿底面半径切开,等分后再拼成一个近似的长方体,这个长方体的长是18.84厘米,高是10厘米,这个圆柱体的体积是多少?表面积是多少? 2.把一个长方体的长缩短3厘米正好变成了一个正方体,这时它的表面积就减少48平方厘米,求原长方体的体积。
小结 今天学到了什么,有什么收获?
(1):
(2):
(3):
作业 (课后余下习题。)
反馈
教材内容 教材第96页内容。
目标 能正确计算常见立体图形的表面积和体积,并解决一些简单的实际问题。
重点 会正确计算立体图体的表面积与体积。
难点 提高学生解决问题的能力,发展学生的空间能力。
过程 引入 立体图形在生活中应用的很广泛,那么我们怎么计算它们的表面积和体积呢?根据所学知识完成下表。 图形名称字母 意义底面 积侧面 积表面 积体积长方 体a一长 b一宽 h-高S=S=S=V=V正方 体a一棱 长S=S=S=V=圆柱S-底 面积 r一底 面半径 h-高 C-底 面周长S=S=S==A圆锥S-底 面积 r一底 面半径 h-高S=S=S=V=
探新 1.在实际生活中立体图形的表面积应如何计算? 2.立体图形的容积和体积计算有什么区别与联系? 学生讨论,教师查看并做出一些指导。 汇报: 表面积:一个立体图形所有面的面积总和叫做它的表面积。 体积:一个立体图形所占空间的大小叫做它的体积。 应用中: 计算表面积要注意一共要算哪几个面的面积。 计算体积要弄清实际情况,计算容积要从容器里面量。
巩固 1. (1)如图,做两个无盖鱼缸,至少各需要多少平方厘米玻璃? (2)哪个鱼缸盛水多,先猜一猜,再计算多多少升? 2.要包装100个圆柱形易拉罐的侧面,至少共需要多少平方分米的广告纸? 2. 1.把一个圆柱体沿底面半径切开,等分后再拼成一个近似的长方体,这个长方体的长是18.84厘米,高是10厘米,这个圆柱体的体积是多少?表面积是多少? 2.把一个长方体的长缩短3厘米正好变成了一个正方体,这时它的表面积就减少48平方厘米,求原长方体的体积。
小结 今天学到了什么,有什么收获?
(1):
(2):
(3):
作业 (课后余下习题。)
反馈
