5.4.2二分查找课件-2021-2022学年浙教版(2019)高中信息技术选修1(21张PPT)
文档属性
| 名称 | 5.4.2二分查找课件-2021-2022学年浙教版(2019)高中信息技术选修1(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-05-10 09:10:30 | ||
图片预览





文档简介
(共21张PPT)
5.4.2 二分查找
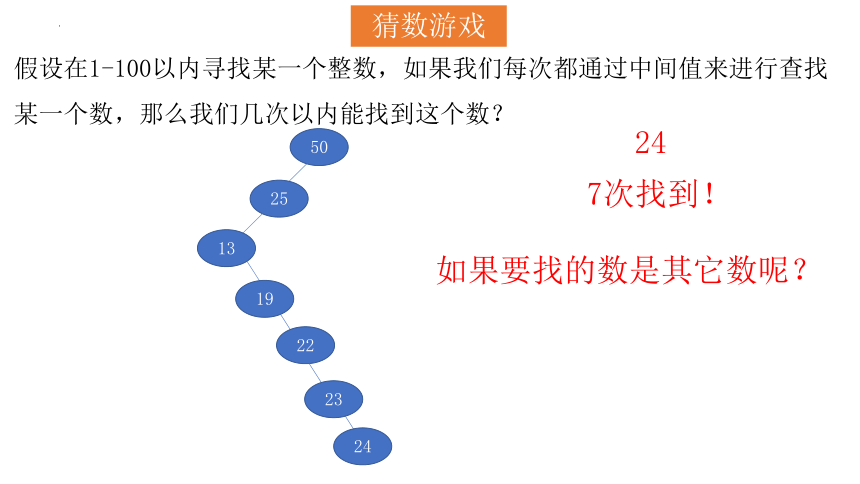
猜数游戏
假设在1-100以内寻找某一个整数,如果我们每次都通过中间值来进行查找
某一个数,那么我们几次以内能找到这个数?
24
50
25
13
19
22
23
24
7次找到!
如果要找的数是其它数呢?
二分查找又称折半查找,对分查找。它是一种效率很高的查找方法,但
被查找的数据序列必须是有序的。
二分查找首先将查找键与有序数组内处于中间位置的元素进行比较,如果
中间位置上的元素的数值与查找键不同,根据数组元素的有序性,就可确
定在数组的前半部分还是后半部分继续查找;在新确定的范围内,继续按
上述方法进行查找,直到获得最终结果。
在数组中的数据是有序的,若是升序的,是指下标越小的数组元素中存储
的数据也越小,降序则相反。为简单起见,设数组d中存储了n个互不相同
的数据,并且数组d中的数据是升序的,则应有:d[0]d[n-1]。
使用两个变量i和j分别记录查找范围内的第一个数组元素和最后一个数组
元素的下标。开始时,整个数组中的所有n个元素都在查找范围内,即变量
i的初值为0,j的初值为n-1,用(i,j)表示查找范围从d[i]起到d[j]为止。
二分查找的基本方法是:在查找范围(i,j)内,可以利用数据的有序性,
而不必逐个地进行查找。
①首先确定该区间的中点位置:m=[(i+j)/2](m表示小于等于的最大整
数)。
②然后将查找键key与d[m]比较,结果必然是如下三种情况之一:
(a)key(b)key=d[m],找到了需要的数据。
(c)key>d[m],由与(a)相同的理由,只需在新的范围(m+1,j)中继续查找。
在通过一次比较后,新的查找范围不会超过上一次查找范围的一半。
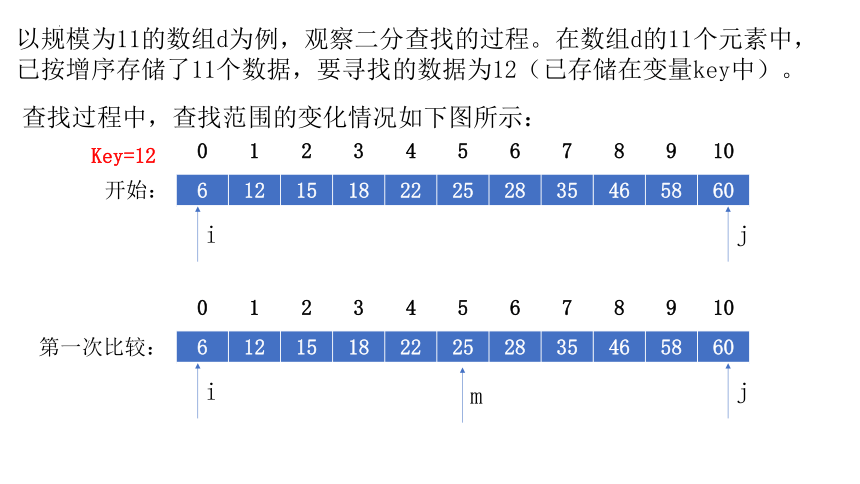
以规模为11的数组d为例,观察二分查找的过程。在数组d的11个元素中,
已按增序存储了11个数据,要寻找的数据为12(已存储在变量key中)。
查找过程中,查找范围的变化情况如下图所示:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
Key=12
开始:
i
j
第一次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
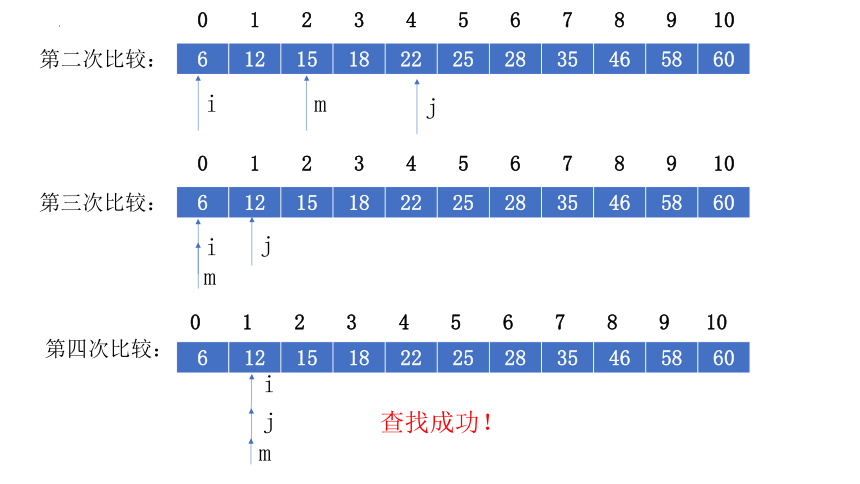
第二次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
第三次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
第四次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
查找成功!
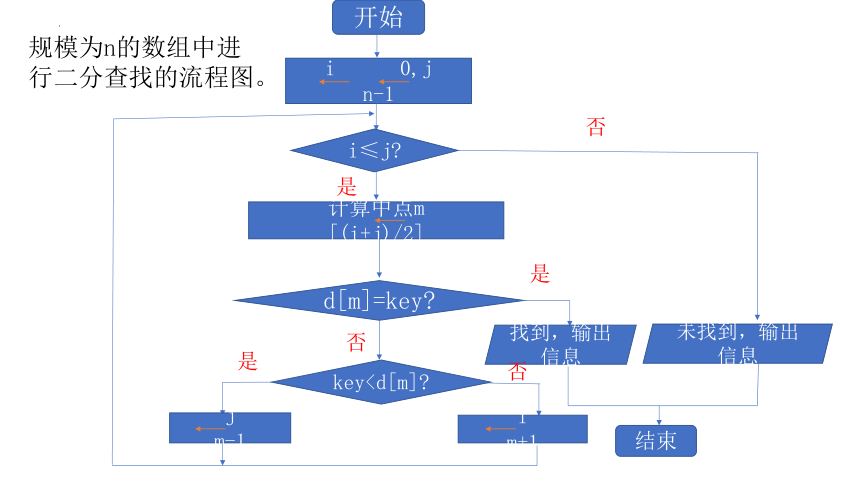
规模为n的数组中进行二分查找的流程图。
开始
i 0,j n-1
i≤j
是
计算中点m [(i+j)/2]
d[m]=key
找到,输出信息
是
否
否
未找到,输出信息
结束
keyj m-1
i m+1
是
否
实现此算法的
Python程序:
key=12
d=[6,12,15,18,22,25,28,35,46,58,60]
f=False
#i和j定义子数组的边界,一开始搜索的是整个数组
i=0
j=len(d)-1
while i<=j:
m=(i+j)//2
if d[m]==key:
f=True
b=m
break
if keyj=m-1
else: #到右边去找
i=m+1
if f==True:
print(“查找成功!第”+str(b)+”个”)
else:
print(“没有找到!”)
另一种写法:
d=[6,12,15,18,22,25,28,35,46,58,60]
i=0
j=len(d)-1
key=int(input(‘请输入查找值:’))
while i<=j:
m=(i+j)//2
if d[m]==key:
print(“找到了,索引位置为:”,m)
break
if keyj=m-1
else: #到右边去找
i=m+1
if i>j:
print(“没有找到!”)
二分查找过程中,在每次关键字比较时,如果不匹配,那么根据匹配结果
将查找表一分为二,排除没有包含查找键的那一半,然后在可能含有查找
键的那一半中继续二分查找,直至找到查找键或找遍整个数组。
处理思想是将一个大范围的查找问题转化为一个与原问题相似的查找范围
较小的查找问题,并且查找能在一定条件下停止。这个思想符合递归算法
的思想。
二分查找算法的递归实现
def bsearch(s,array):
if len(array)==0:
print(“未找到!”)
return False
mid=(len(array)-1)//2
if array[mid]==s:
print(“找到了!”)
return True
elif sreturn bsearch(s,array[:mid])
else:
return bsearch(s,array[mid+1:])
key=12
d=[6,12,15,18,22,25,28,35,46,58,60]
print(bsearch(key,d))
若查找对象采用链表结构,能否适用二分查找?
一般而言,链表结构不适合采用二分查找,但这又并非绝对,链表结构
可以通过数组来实现,从而二分查找也适用。
二分查找过程可用一棵二叉树来描述,树中的每个根节点对应当前查找区间
的中点元素,它的左子树和右子树分别对应该区间的左子表和右子表,如下
图所示:
25
15
6
12
18
22
46
28
35
58
60
二分查找的判定树实例
查找key为12的元素
比较次数为4次
结论:在n个元素排序的顺序表里,某一次查找过程中,所做比较次数不
超过判定树的高度加1,即[]+1
由于二分查找在有序表上进行,所以其对应的判定树就是一棵二叉排序树。
二叉排序树也称为二叉查找树,这种结构的二叉树既能实现排序功能,
也能实现查找功能。
一、排序
二叉排序树的排序功能主要通过二叉树的建立和遍历过程来实现,其在建立
过程中要始终满足如下性质:
1.若它的左子树不为空,则左子树上的所有节点的值均小于它的根节点的值。
2.若它的右子树不为空,则右子树上所有节点的值均大于它的根节点的值。
3.它的左右子树也分别为二叉排序树。
一组数据“23,20,13,18,14,11”建立的二叉排序树如下图所示,对此
二叉树进行中序遍历时,结果为从小到大的有序序列:
23
20
13
11
18
14
11,13,14,18,20,23
二、查找
二叉查找树的查找过程为:首先将给定值和根节点的关键字比较,若相等,
则查找成功;若不相等,则根据给定值和根节点关键字之间的大小关系,
在左子树或右子树中继续进行查找。若查到为空树时,说明该树中没有待查
记录,故查找不成功。
23
20
13
11
18
14
查找关键字key为14的节点
小
小
大
小
路径:23 20 13 18 14
与给定值比较的关键字个数不超过树的高度加1,
即[]+1。
练一练:
1.在有序数组[12,23,34,45,46,56,75,81,87,99]中查找数据87,左偏取
中间位置元素,则数组中被比较的数字可能是( )
A.46,81,87
B.46,99,81,87
C.99,87
D.56,75,99,87
A
2.在含有20个数据的数组中使用二分查找算法查找某个元素,若查找失败,
则进行比较的次数是( )
A.5
B.10
C.15
D.20
A
谢 谢
5.4.2 二分查找
猜数游戏
假设在1-100以内寻找某一个整数,如果我们每次都通过中间值来进行查找
某一个数,那么我们几次以内能找到这个数?
24
50
25
13
19
22
23
24
7次找到!
如果要找的数是其它数呢?
二分查找又称折半查找,对分查找。它是一种效率很高的查找方法,但
被查找的数据序列必须是有序的。
二分查找首先将查找键与有序数组内处于中间位置的元素进行比较,如果
中间位置上的元素的数值与查找键不同,根据数组元素的有序性,就可确
定在数组的前半部分还是后半部分继续查找;在新确定的范围内,继续按
上述方法进行查找,直到获得最终结果。
在数组中的数据是有序的,若是升序的,是指下标越小的数组元素中存储
的数据也越小,降序则相反。为简单起见,设数组d中存储了n个互不相同
的数据,并且数组d中的数据是升序的,则应有:d[0]
使用两个变量i和j分别记录查找范围内的第一个数组元素和最后一个数组
元素的下标。开始时,整个数组中的所有n个元素都在查找范围内,即变量
i的初值为0,j的初值为n-1,用(i,j)表示查找范围从d[i]起到d[j]为止。
二分查找的基本方法是:在查找范围(i,j)内,可以利用数据的有序性,
而不必逐个地进行查找。
①首先确定该区间的中点位置:m=[(i+j)/2](m表示小于等于的最大整
数)。
②然后将查找键key与d[m]比较,结果必然是如下三种情况之一:
(a)key
(c)key>d[m],由与(a)相同的理由,只需在新的范围(m+1,j)中继续查找。
在通过一次比较后,新的查找范围不会超过上一次查找范围的一半。
以规模为11的数组d为例,观察二分查找的过程。在数组d的11个元素中,
已按增序存储了11个数据,要寻找的数据为12(已存储在变量key中)。
查找过程中,查找范围的变化情况如下图所示:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
Key=12
开始:
i
j
第一次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
第二次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
第三次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
第四次比较:
6 12 15 18 22 25 28 35 46 58 60
0 1 2 3 4 5 6 7 8 9 10
i
j
m
查找成功!
规模为n的数组中进行二分查找的流程图。
开始
i 0,j n-1
i≤j
是
计算中点m [(i+j)/2]
d[m]=key
找到,输出信息
是
否
否
未找到,输出信息
结束
key
i m+1
是
否
实现此算法的
Python程序:
key=12
d=[6,12,15,18,22,25,28,35,46,58,60]
f=False
#i和j定义子数组的边界,一开始搜索的是整个数组
i=0
j=len(d)-1
while i<=j:
m=(i+j)//2
if d[m]==key:
f=True
b=m
break
if key
else: #到右边去找
i=m+1
if f==True:
print(“查找成功!第”+str(b)+”个”)
else:
print(“没有找到!”)
另一种写法:
d=[6,12,15,18,22,25,28,35,46,58,60]
i=0
j=len(d)-1
key=int(input(‘请输入查找值:’))
while i<=j:
m=(i+j)//2
if d[m]==key:
print(“找到了,索引位置为:”,m)
break
if key
else: #到右边去找
i=m+1
if i>j:
print(“没有找到!”)
二分查找过程中,在每次关键字比较时,如果不匹配,那么根据匹配结果
将查找表一分为二,排除没有包含查找键的那一半,然后在可能含有查找
键的那一半中继续二分查找,直至找到查找键或找遍整个数组。
处理思想是将一个大范围的查找问题转化为一个与原问题相似的查找范围
较小的查找问题,并且查找能在一定条件下停止。这个思想符合递归算法
的思想。
二分查找算法的递归实现
def bsearch(s,array):
if len(array)==0:
print(“未找到!”)
return False
mid=(len(array)-1)//2
if array[mid]==s:
print(“找到了!”)
return True
elif s
else:
return bsearch(s,array[mid+1:])
key=12
d=[6,12,15,18,22,25,28,35,46,58,60]
print(bsearch(key,d))
若查找对象采用链表结构,能否适用二分查找?
一般而言,链表结构不适合采用二分查找,但这又并非绝对,链表结构
可以通过数组来实现,从而二分查找也适用。
二分查找过程可用一棵二叉树来描述,树中的每个根节点对应当前查找区间
的中点元素,它的左子树和右子树分别对应该区间的左子表和右子表,如下
图所示:
25
15
6
12
18
22
46
28
35
58
60
二分查找的判定树实例
查找key为12的元素
比较次数为4次
结论:在n个元素排序的顺序表里,某一次查找过程中,所做比较次数不
超过判定树的高度加1,即[]+1
由于二分查找在有序表上进行,所以其对应的判定树就是一棵二叉排序树。
二叉排序树也称为二叉查找树,这种结构的二叉树既能实现排序功能,
也能实现查找功能。
一、排序
二叉排序树的排序功能主要通过二叉树的建立和遍历过程来实现,其在建立
过程中要始终满足如下性质:
1.若它的左子树不为空,则左子树上的所有节点的值均小于它的根节点的值。
2.若它的右子树不为空,则右子树上所有节点的值均大于它的根节点的值。
3.它的左右子树也分别为二叉排序树。
一组数据“23,20,13,18,14,11”建立的二叉排序树如下图所示,对此
二叉树进行中序遍历时,结果为从小到大的有序序列:
23
20
13
11
18
14
11,13,14,18,20,23
二、查找
二叉查找树的查找过程为:首先将给定值和根节点的关键字比较,若相等,
则查找成功;若不相等,则根据给定值和根节点关键字之间的大小关系,
在左子树或右子树中继续进行查找。若查到为空树时,说明该树中没有待查
记录,故查找不成功。
23
20
13
11
18
14
查找关键字key为14的节点
小
小
大
小
路径:23 20 13 18 14
与给定值比较的关键字个数不超过树的高度加1,
即[]+1。
练一练:
1.在有序数组[12,23,34,45,46,56,75,81,87,99]中查找数据87,左偏取
中间位置元素,则数组中被比较的数字可能是( )
A.46,81,87
B.46,99,81,87
C.99,87
D.56,75,99,87
A
2.在含有20个数据的数组中使用二分查找算法查找某个元素,若查找失败,
则进行比较的次数是( )
A.5
B.10
C.15
D.20
A
谢 谢
