6-2平行四边形的判定(2)课件--北师大版八年级数学下册(21张ppt)
文档属性
| 名称 | 6-2平行四边形的判定(2)课件--北师大版八年级数学下册(21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 242.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 19:11:28 | ||
图片预览




文档简介
(共21张PPT)
6.2 平行四边形的判定
(第2课时)
1. 利用对角线互相平分判定平行四边形.
2. 掌握平行四边形判定的方法.
教学目标
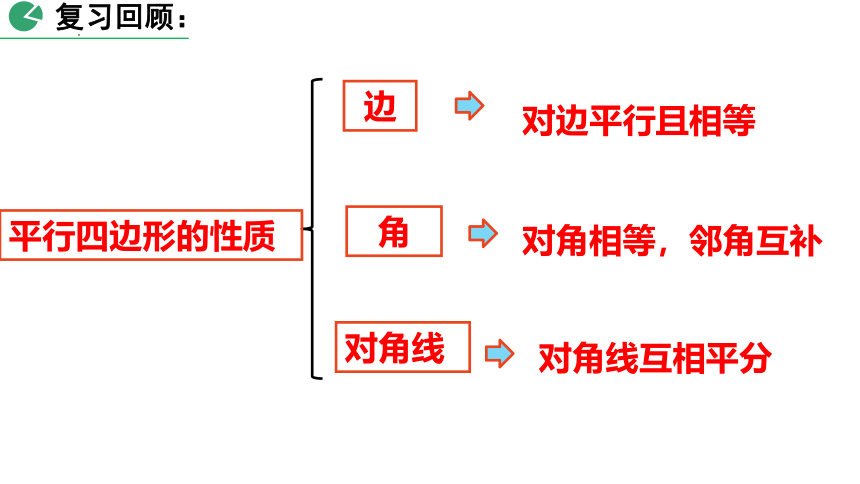
边
对角线
平行四边形的性质
角
对边平行且相等
对角相等,邻角互补
对角线互相平分
复习回顾:
2、两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是 平行四边形
3、一组对边平行且相等的四边形是平行四边形
∵AB=CD, AB∥CD,
∴四边形ABCD是 平行四边形
平行四边形判定方法
复习回顾:
1、两组对边分别平行的四边形是平行四边形
∵ AB∥CD AD∥BC
∴四边形ABCD是 平行四边形
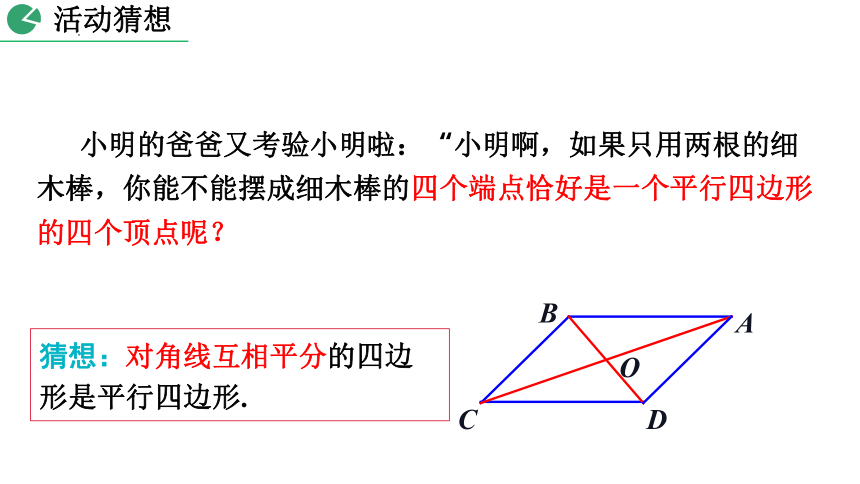
小明的爸爸又考验小明啦:“小明啊,如果只用两根的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
活动猜想
A
B
C
D
O
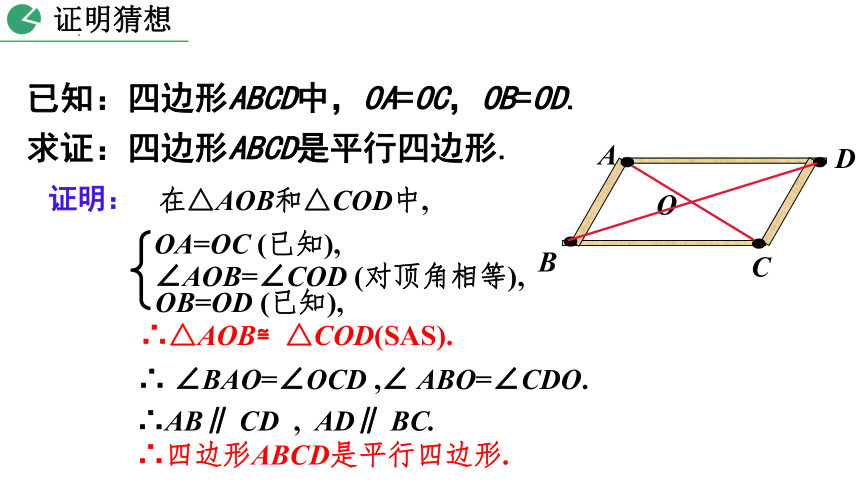
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
证明猜想
对角线互相平分的四边形是平行四边形.
∵AO=CO,
BO=DO,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理3
A
B
C
D
O
结论
探究新知
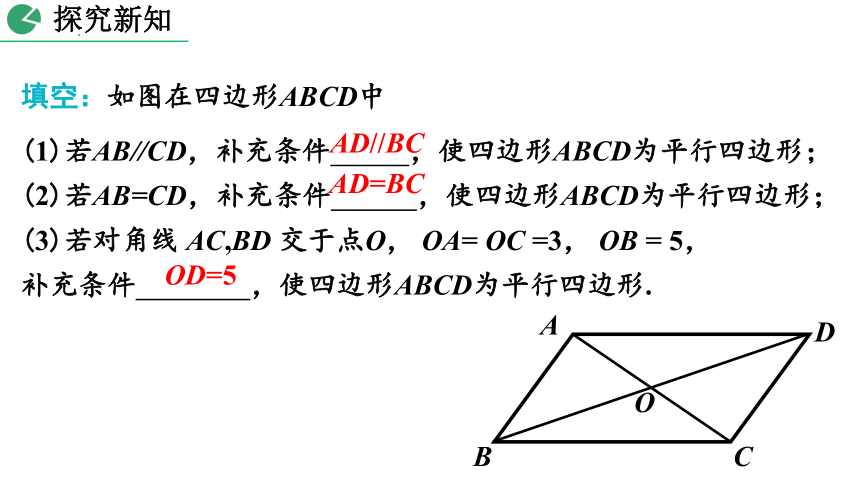
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形;
(3)若对角线 AC,BD 交于点O, OA= OC =3, OB = 5,
补充条件 ,使四边形ABCD为平行四边形.
AD//BC
AD=BC
OD=5
B
O
D
A
C
探究新知
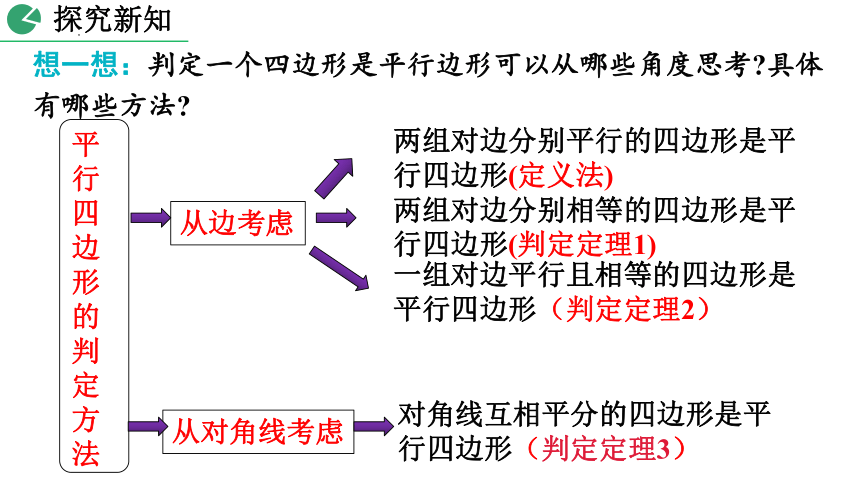
想一想:判定一个四边形是平行边形可以从哪些角度思考 具体有哪些方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从对角线考虑
平行四边形的判定方法
对角线互相平分的四边形是平行四边形(判定定理3)
探究新知
例题 已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF,
∴AO-AE=CO-CF.
∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
O
B
A
C
E
F
D
探究新知
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
拓展延伸
对于上述例题,若点E、F 继续移动至 OA、OC 的延长线上,仍使AE=CF(如图),那么结论还成立吗?若不成立,,请说明理由,若成立请证明。
B
E
F
A
C
D
O
判定平行四边形的方法选择
已知条件 证明思路
一组对边相等 1.另一组对边也相等
2.相等的边也平行
一组对边平行 1.另一组对边也平行
2.平行的边也相等
对角线相交 对角线互相平分
探究新知
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形;
(2)若AC=8cm,BD=10cm,那么当AO=___cm,DO=___cm时,四边形ABCD为平行四边形.
8
4
4
5
当堂检测
2. 对于四边形ABCD,如果从条件①AB∥CD②AD∥BC③AB=CD④BC=AD中选出2个,那么能说明四边形ABCD是平行四边形的有_______(填序号,填出符合条件的一种情况即可)
3、根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
当堂检测
4.已知:如图,平行四边形ABCD的对角线AC与BD于点O,E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
B
C
A
D
E
F
O
当堂检测
5、如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
当堂检测
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
6、已知:如图, ABCD中,E、F分别是AC上两点,且BE⊥AC 于E,DF⊥AC 于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
当堂检测
如图,已知G,H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG,FH交于点D,连接AD,DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
巩固练习
证明: ∵GE∥BH,HF∥BG,∴四边形BHDG是平行四边形.
∴OB= OD,OG= OH.
∵G,H是△ABC的边AC的三等分点,∴AG=GH=CH.
∴OG+ AG =OH+ CH, ∴OA= OC,
∴四边形ABCD是平行四边形.
巩固练习
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从对角线考虑
平行四边形的判定方法
对角线互相平分的四边形是平行四边形(判定定理3)
6.2 平行四边形的判定
(第2课时)
1. 利用对角线互相平分判定平行四边形.
2. 掌握平行四边形判定的方法.
教学目标
边
对角线
平行四边形的性质
角
对边平行且相等
对角相等,邻角互补
对角线互相平分
复习回顾:
2、两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是 平行四边形
3、一组对边平行且相等的四边形是平行四边形
∵AB=CD, AB∥CD,
∴四边形ABCD是 平行四边形
平行四边形判定方法
复习回顾:
1、两组对边分别平行的四边形是平行四边形
∵ AB∥CD AD∥BC
∴四边形ABCD是 平行四边形
小明的爸爸又考验小明啦:“小明啊,如果只用两根的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
活动猜想
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
证明猜想
对角线互相平分的四边形是平行四边形.
∵AO=CO,
BO=DO,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理3
A
B
C
D
O
结论
探究新知
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形;
(3)若对角线 AC,BD 交于点O, OA= OC =3, OB = 5,
补充条件 ,使四边形ABCD为平行四边形.
AD//BC
AD=BC
OD=5
B
O
D
A
C
探究新知
想一想:判定一个四边形是平行边形可以从哪些角度思考 具体有哪些方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从对角线考虑
平行四边形的判定方法
对角线互相平分的四边形是平行四边形(判定定理3)
探究新知
例题 已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF,
∴AO-AE=CO-CF.
∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
O
B
A
C
E
F
D
探究新知
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
拓展延伸
对于上述例题,若点E、F 继续移动至 OA、OC 的延长线上,仍使AE=CF(如图),那么结论还成立吗?若不成立,,请说明理由,若成立请证明。
B
E
F
A
C
D
O
判定平行四边形的方法选择
已知条件 证明思路
一组对边相等 1.另一组对边也相等
2.相等的边也平行
一组对边平行 1.另一组对边也平行
2.平行的边也相等
对角线相交 对角线互相平分
探究新知
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形;
(2)若AC=8cm,BD=10cm,那么当AO=___cm,DO=___cm时,四边形ABCD为平行四边形.
8
4
4
5
当堂检测
2. 对于四边形ABCD,如果从条件①AB∥CD②AD∥BC③AB=CD④BC=AD中选出2个,那么能说明四边形ABCD是平行四边形的有_______(填序号,填出符合条件的一种情况即可)
3、根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
当堂检测
4.已知:如图,平行四边形ABCD的对角线AC与BD于点O,E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
B
C
A
D
E
F
O
当堂检测
5、如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
当堂检测
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
6、已知:如图, ABCD中,E、F分别是AC上两点,且BE⊥AC 于E,DF⊥AC 于F.
求证:四边形BEDF是平行四边形.
┓
┓
A
B
C
D
E
F
当堂检测
如图,已知G,H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG,FH交于点D,连接AD,DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
巩固练习
证明: ∵GE∥BH,HF∥BG,∴四边形BHDG是平行四边形.
∴OB= OD,OG= OH.
∵G,H是△ABC的边AC的三等分点,∴AG=GH=CH.
∴OG+ AG =OH+ CH, ∴OA= OC,
∴四边形ABCD是平行四边形.
巩固练习
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从对角线考虑
平行四边形的判定方法
对角线互相平分的四边形是平行四边形(判定定理3)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
