12-1定义与命题课件苏科版数学七年级下册(16张ppt)
文档属性
| 名称 | 12-1定义与命题课件苏科版数学七年级下册(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 730.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
学习目标:
1.什么是定义?
2.什么是命题,结构是怎样的?
3.什么是真命题?什么是假命题?
4.如何说明一个命题是假命题?
12.1 定义与命题
情境引入:
篮球比赛中我们常听到解说员说:
“好,漂亮!很快就要进球了,可惜,对方盖帽了。”
生活中为了交流不产生歧义,常常需要使用许多名称和术语,对这些名称的术语和名称的含义必须有明确的规定。
对 名称或术语 的含义 进行描述 或 作出规定,
就是给出它们的 定义。
①在同一平面内,不相交的两条直线是平行线。
②数轴上表示一个点到原点的距离是这个数的绝对值。
③能使方程两边的值相等的未知数的值就是方程的解。
问题一:请你解释下面的名称或术语。
①平行线 ②绝对值 ③方程的解
探索新知:——定义
(1)“等角的余角相等。”与“等角的余角相等吗 ”
这两句话一样吗 如果不一样,它们有什么不同
(2)“经过一点有且只有一条直线与已知直线垂直。”与
“经过一点画已知直线的垂线。”有什么不同
判断 一件事情的句子叫做 命题。
要求:1min独立思考,
1生口答
探索新知:——命题的定义
问题二:
1.下列句子中,请选出哪些是命题?
A、对顶角相等。
B、延长线段AB到点C,使BC=AB。
C、两直线平行,同位角相等。
D、同位角相等吗?
E、四边形不是多边形。
F、立正!
不是(作图语句)
是
不是(疑问句)
是
不是(祈使句)
是
是否作出判断
采用:腾讯课堂答题卡
提交正确选项
思考:你认为判断一句话是否是命题的关键是什么?
练习:(多选题)
(2)一定不是命题的语句:
1.疑问句?
3.作图语句
(如:过...作...或延长...或连接...)
2.祈使句
(1)凡做出判断的陈述句都是命题,
不论判断是否正确;
归纳总结:——判断命题的方法
(2)如果 ,那么 。
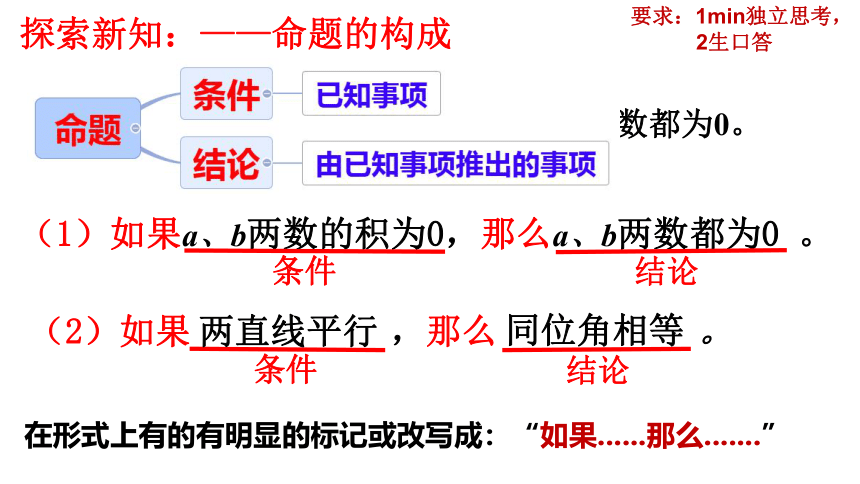
(2)两直线平行,同位角相等。
(1)如果a、b两数的积为0,那么a、b两数都为0 。
条件
结论
判断下列句子是否是命题:
(1)如果a、b两数的积为0,那么a、b两数都为0。
要求:1min独立思考,
2生口答
条件
结论
两直线平行
同位角相等
探索新知:——命题的构成
在形式上有的有明显的标记或改写成:“如果......那么.......”
2.下列命题的条件是什么?结论是什么?
C、同旁内角互补,两直线平行.
A、相等的角是对顶角.
B、平行于同一条直线的两条不同的直线平行.
条件:
结论:
条件: 结论:
条件: 结论:
两直线平行
两个角相等
这两个角是对顶角
两条直线平行于同一条直线
两条不同的直线平行
(若是命题则试着改成“如果...那么...”的形式)
思考:这些命题中若条件成立,结论是否成立?
请选出条件成立,结论也成立的命题( )
同旁内角互补
练习:
真命题 如果条件成立,结论成立
假命题 如果条件成立,但结论不成立
说明假命题的常用方法:
举一个反例
归纳总结:——命题的分类
说明真命题的常用方法:
证明
3.下列命题中真命题是( )若是假命题,请举出反例
A、末位数字是5的整数,能被5整除。
B、如果两个角是对顶角,那么它们的平分线组成一个平角。
C、平方后等于4的数是2。
D、锐角与钝角互为补角。
真命题
真命题
假命题
假命题
举出一个符合命题的条件,但是命题结论不成立的例子来说明命题是假命题,这样的例子成为反例。
采用:腾讯课堂答题卡
提交正确选项
练习(多选题)
解答题:
本节课你学会了……
课堂小结:
对于同一平面内的三条直线a、b、c,给出下列五个论断:
(1)a∥b;(2)b∥c;(3)a⊥b;
(4)a∥c;(5)a⊥c ;
以其中两个论断为条件,一个论断为结论,组成一个真命题(至少写出3个).
中午练习1:
下列各命题的条件是什么?结论是什么?并判断下列命题的真假
(1)如果a、b两数的积为0,那么a、b两数都为0。
(2)如果两个角互为补角,那么这两角和为180°。
(3)两直线平行,同旁内角互补。
(4)两条直线相交,只有一个交点。
(5)有公共端点的两个角是对顶角。
条件 结论
1
2
3
4
5
中午
练习2:
真命题
真命题
真命题
假命题
假命题
a、b两数的积为0
a、b两数都为0
两个角互为补角
这两角和为180°
两直线平行
同旁内角互补
两条直线相交
这两条直线只有一个交点
有公共端点的两个角
这两个角是对顶角
1.直线外一点到直线的垂线段的长度,叫做_________的距离.
2.下列句子中,不是命题的是( )
A.三角形的内角和等于180° B.对顶角相等
C.过一点作已知直线的垂线 D.同旁内角互补
3.下列命题中,假命题是( )
A.对顶角相等 B.两直线平行,同位角相等
C.互补两角的和等于180° D.内错角相等
4. 下列命题中的真命题是( )
A.锐角大于它的余角 B.锐角大于它的补角
C.钝角大于它的补角 D.锐角与钝角之和等于平角
点到直线
C
D
C
中午练习3:(限时8分钟)
这两个角是对顶角
5.写出下列命题的条件和结论,并判断是真命题还是假命题?
①两直线平行,同旁内角互补;
条件:________________,结论:________________是____命题.
②同角的补角相等;
条件:________________ ,结论:____________是__命题.
③命题“相等的角是对顶角” .
条件:________________,结论:________________是____命题.
两条直线平行
内错角相等
真
两个角是同一个角的补角
这两个角相等
真
假
两个角相等
学习目标:
1.什么是定义?
2.什么是命题,结构是怎样的?
3.什么是真命题?什么是假命题?
4.如何说明一个命题是假命题?
12.1 定义与命题
情境引入:
篮球比赛中我们常听到解说员说:
“好,漂亮!很快就要进球了,可惜,对方盖帽了。”
生活中为了交流不产生歧义,常常需要使用许多名称和术语,对这些名称的术语和名称的含义必须有明确的规定。
对 名称或术语 的含义 进行描述 或 作出规定,
就是给出它们的 定义。
①在同一平面内,不相交的两条直线是平行线。
②数轴上表示一个点到原点的距离是这个数的绝对值。
③能使方程两边的值相等的未知数的值就是方程的解。
问题一:请你解释下面的名称或术语。
①平行线 ②绝对值 ③方程的解
探索新知:——定义
(1)“等角的余角相等。”与“等角的余角相等吗 ”
这两句话一样吗 如果不一样,它们有什么不同
(2)“经过一点有且只有一条直线与已知直线垂直。”与
“经过一点画已知直线的垂线。”有什么不同
判断 一件事情的句子叫做 命题。
要求:1min独立思考,
1生口答
探索新知:——命题的定义
问题二:
1.下列句子中,请选出哪些是命题?
A、对顶角相等。
B、延长线段AB到点C,使BC=AB。
C、两直线平行,同位角相等。
D、同位角相等吗?
E、四边形不是多边形。
F、立正!
不是(作图语句)
是
不是(疑问句)
是
不是(祈使句)
是
是否作出判断
采用:腾讯课堂答题卡
提交正确选项
思考:你认为判断一句话是否是命题的关键是什么?
练习:(多选题)
(2)一定不是命题的语句:
1.疑问句?
3.作图语句
(如:过...作...或延长...或连接...)
2.祈使句
(1)凡做出判断的陈述句都是命题,
不论判断是否正确;
归纳总结:——判断命题的方法
(2)如果 ,那么 。
(2)两直线平行,同位角相等。
(1)如果a、b两数的积为0,那么a、b两数都为0 。
条件
结论
判断下列句子是否是命题:
(1)如果a、b两数的积为0,那么a、b两数都为0。
要求:1min独立思考,
2生口答
条件
结论
两直线平行
同位角相等
探索新知:——命题的构成
在形式上有的有明显的标记或改写成:“如果......那么.......”
2.下列命题的条件是什么?结论是什么?
C、同旁内角互补,两直线平行.
A、相等的角是对顶角.
B、平行于同一条直线的两条不同的直线平行.
条件:
结论:
条件: 结论:
条件: 结论:
两直线平行
两个角相等
这两个角是对顶角
两条直线平行于同一条直线
两条不同的直线平行
(若是命题则试着改成“如果...那么...”的形式)
思考:这些命题中若条件成立,结论是否成立?
请选出条件成立,结论也成立的命题( )
同旁内角互补
练习:
真命题 如果条件成立,结论成立
假命题 如果条件成立,但结论不成立
说明假命题的常用方法:
举一个反例
归纳总结:——命题的分类
说明真命题的常用方法:
证明
3.下列命题中真命题是( )若是假命题,请举出反例
A、末位数字是5的整数,能被5整除。
B、如果两个角是对顶角,那么它们的平分线组成一个平角。
C、平方后等于4的数是2。
D、锐角与钝角互为补角。
真命题
真命题
假命题
假命题
举出一个符合命题的条件,但是命题结论不成立的例子来说明命题是假命题,这样的例子成为反例。
采用:腾讯课堂答题卡
提交正确选项
练习(多选题)
解答题:
本节课你学会了……
课堂小结:
对于同一平面内的三条直线a、b、c,给出下列五个论断:
(1)a∥b;(2)b∥c;(3)a⊥b;
(4)a∥c;(5)a⊥c ;
以其中两个论断为条件,一个论断为结论,组成一个真命题(至少写出3个).
中午练习1:
下列各命题的条件是什么?结论是什么?并判断下列命题的真假
(1)如果a、b两数的积为0,那么a、b两数都为0。
(2)如果两个角互为补角,那么这两角和为180°。
(3)两直线平行,同旁内角互补。
(4)两条直线相交,只有一个交点。
(5)有公共端点的两个角是对顶角。
条件 结论
1
2
3
4
5
中午
练习2:
真命题
真命题
真命题
假命题
假命题
a、b两数的积为0
a、b两数都为0
两个角互为补角
这两角和为180°
两直线平行
同旁内角互补
两条直线相交
这两条直线只有一个交点
有公共端点的两个角
这两个角是对顶角
1.直线外一点到直线的垂线段的长度,叫做_________的距离.
2.下列句子中,不是命题的是( )
A.三角形的内角和等于180° B.对顶角相等
C.过一点作已知直线的垂线 D.同旁内角互补
3.下列命题中,假命题是( )
A.对顶角相等 B.两直线平行,同位角相等
C.互补两角的和等于180° D.内错角相等
4. 下列命题中的真命题是( )
A.锐角大于它的余角 B.锐角大于它的补角
C.钝角大于它的补角 D.锐角与钝角之和等于平角
点到直线
C
D
C
中午练习3:(限时8分钟)
这两个角是对顶角
5.写出下列命题的条件和结论,并判断是真命题还是假命题?
①两直线平行,同旁内角互补;
条件:________________,结论:________________是____命题.
②同角的补角相等;
条件:________________ ,结论:____________是__命题.
③命题“相等的角是对顶角” .
条件:________________,结论:________________是____命题.
两条直线平行
内错角相等
真
两个角是同一个角的补角
这两个角相等
真
假
两个角相等
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
