青岛版八年级数学下册 10.2一次函数和它的图象 课件(共15张)
文档属性
| 名称 | 青岛版八年级数学下册 10.2一次函数和它的图象 课件(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
10.2 一次函数和它的图象
八年级数学
第10章 一次函数
学习目标:
1、掌握一次函数的概念,理解一次函数与正比例函数的区别与联系;
2、会用待定系数法求一次函数的解析式;
3、 根据解析式画出一次函数的图象,并利用图象解决问题;
4、渗透“数形结合”思想,发展学生的数学能力;
【重、难点】一次函数的图象与应用
观察五个函数关系式完成下列填空:
课堂导入:
y=x+0.5
y=x-1
1、这些函数都有 个变量,
自变量的次数都为 ,
自变量的系数 0(填=, ≠)。
2、这些函数表达式都是自变量的 次式,
它们的一般形式是 。
1
2
y=kx+b
≠
一
一列高铁列车自北京站出发,运行10km 后,便以300km∕h的速度匀速行驶。如果从运行10km后开始计时,你能写出该列车离开浦东机场站的距离s(单位:米)与时间t(单位:秒)之间的函数关系式吗?
S=10+300t
某同学的家离学校2000米,骑自行车返校时他每分钟行驶200米。他骑车所用的时间X(分钟)与剩下的路程Y(米)之间的函数关系式为 。
y=2000-200x
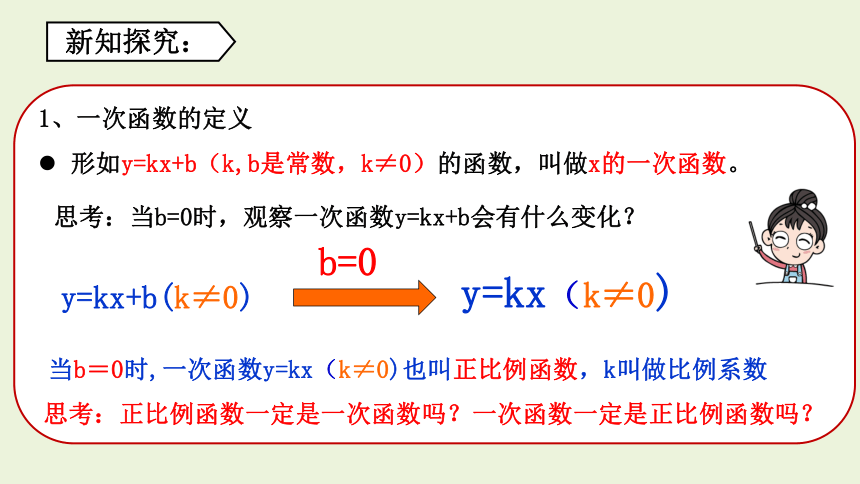
1、一次函数的定义
形如y=kx+b(k,b是常数,k≠0)的函数,叫做x的一次函数。
y=kx+b(k≠0)
当b=0时,一次函数y=kx(k≠0)也叫正比例函数,k叫做比例系数
新知探究:
b=0
y=kx(k≠0)
思考:当b=0时,观察一次函数y=kx+b会有什么变化?
思考:正比例函数一定是一次函数吗?一次函数一定是正比例函数吗?
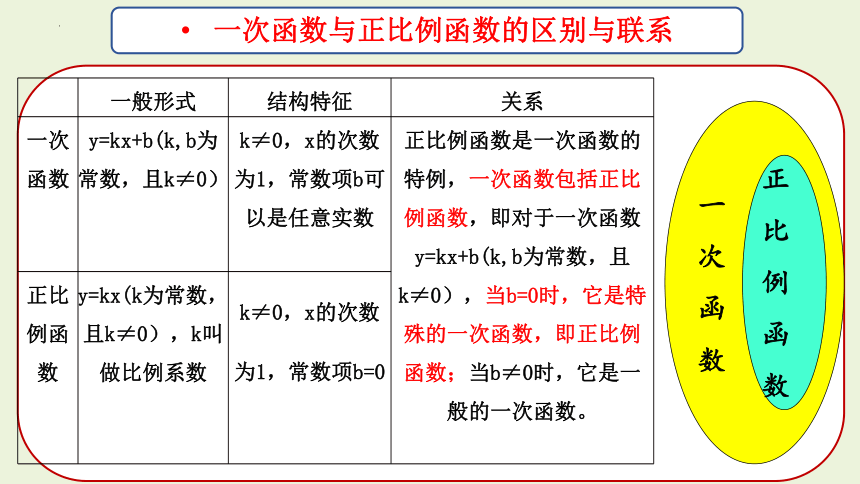
一般形式 结构特征 关系
一次函数 y=kx+b(k,b为常数,且k≠0) k≠0,x的次数为1,常数项b可以是任意实数 正比例函数是一次函数的特例,一次函数包括正比例函数,即对于一次函数y=kx+b(k,b为常数,且k≠0),当b=0时,它是特殊的一次函数,即正比例函数;当b≠0时,它是一般的一次函数。
正比例函数 y=kx(k为常数,且k≠0),k叫做比例系数 k≠0,x的次数为1,常数项b=0
一次函数与正比例函数的区别与联系
一
次
函
数
正
比
例
函
数
当堂练习:下列函数中,哪些是一次函数,哪些是正比例函数?
是一次函数,也是正比例函数。
是一次函数,不是正比例函数。
不是一次函数,也不是正比例函数。
是一次函数,不是正比例函数。
不是一次函数,也不是正比例函数
是一次函数,不是正比例函数。
2、要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
3.已知下列函数:y=2x+1,s=60t,y=100-25x, , ,其中表示一次函数的有 个
4、下列说法不正确的是 ( )
A、一次函数不一定是正比例函数 B、不是一次函数就一定不是正比例函数
C、正比例函数是特定的一次函数 D、不是正比例函数就不是一次函数
4
D
题型一 利用一次函数的概念求字母的值
1、y=(m-2)xn-1+n是关于x的一次函数,m、n应满足 。
2、函数y=(2-m)x+2m-3,当m= 时,此函数为正比例函数,当m 时,此函数为一次函数
≠2
m≠2且n=3
新知探究:
思考 已知一次函数的图象经过点(3,5)与(-4,-9),如何求这个一次函数的解析式呢?
解:设这个一次函数的解析式为y=kx+b
∵y=kx+b的图象过点(3,5)与(-4,-9)
∴ 3k+b=5
-4k+b=-9
∴这个一次函数的解析式为y=2x-1
解得 k=2
b=-1
待定系数法:通过先设出表达式中的未知系数,再根据所给条件,利用解方程或方程组确定这些未知系数。
题型二 确定一次函数的表达式
1、已知y+1与x-2成正比例,当x=3时,y=-3,求y与x的函数关系式
解:∵ y+1与x-2成正比例 ∴设这个一函数的解析式为y+1=k(x-2)
∵当x=3时,y=-3 ∴ - 3+1=k(3-2) 解得 k=-2
∴这个一次函数的解析式为y=-2x+3
2、已知函数y=kx+2,当x=2时,y值为4,求k的值。
解:把x=2,y=4代入y=kx+2 得:4=2k+2 ∴k=1
3、若一次函数的图象经过点A(2,1),B(-1,-3),C(m,3),求m的值。
例 汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围,y是x的一次函数吗
题型三 一次函数解析式的简单应用
解:由题意得,函数关系式为y=50-5t,自变量x的取值范围是0≤t≤10,所以,y是x的一次函数
对于日常生活中的实际问题,解题的关键是把问题转化成数学问题,即构建相应的数学模型,建立函数关系式,通过题中条件做出答案。
我们来探究函数y=x-1的图像.
(1)给定自变量的x的一些值,求出对应y的值,并填表;
(2)以x与y的对应值作为点的坐标描出这些点;
(3)按照自变量由小到大的顺序把描出的点顺次连接起来.
如图,可得函数y=x-1的图像.
通过画图,你发现一次函数的图象是什么形状?怎样简单快速的画出一次函数的图象?
y=x-1
新知探究:
三、一次函数的图象
1、图象的形状
一次函数y=kx+b的图象是一条直线,所以也称为直线y=kx+b
2、图象的画法
一次函数的图象是一条直线,而两点确定一条直线,所以画一次函数的图象只要找出图像上的两个点,过这两个点作直线就是所求的一次函数的图象
新知探究:
练习:在同一坐标系中,画出一次函数y=2x+1与y=-2x的图象
题型三:一次函数的图象与坐标轴围成的三角形面积问题
例 已知一次函数y=kx+2的图象与x轴交于点A,与y轴交于点B,且S△OAB=3,求k的值.
课堂小结:
1、一次函数的定义
2、正比例函数是特殊的一次函数
3、对于日常生活中的实际问题,解题的关键是把问题转化成数学问题,即构建相应的数学模型,建立函数关系式,通过题中条件做出答案。
4、一次函数的图象形状与画法
10.2 一次函数和它的图象
八年级数学
第10章 一次函数
学习目标:
1、掌握一次函数的概念,理解一次函数与正比例函数的区别与联系;
2、会用待定系数法求一次函数的解析式;
3、 根据解析式画出一次函数的图象,并利用图象解决问题;
4、渗透“数形结合”思想,发展学生的数学能力;
【重、难点】一次函数的图象与应用
观察五个函数关系式完成下列填空:
课堂导入:
y=x+0.5
y=x-1
1、这些函数都有 个变量,
自变量的次数都为 ,
自变量的系数 0(填=, ≠)。
2、这些函数表达式都是自变量的 次式,
它们的一般形式是 。
1
2
y=kx+b
≠
一
一列高铁列车自北京站出发,运行10km 后,便以300km∕h的速度匀速行驶。如果从运行10km后开始计时,你能写出该列车离开浦东机场站的距离s(单位:米)与时间t(单位:秒)之间的函数关系式吗?
S=10+300t
某同学的家离学校2000米,骑自行车返校时他每分钟行驶200米。他骑车所用的时间X(分钟)与剩下的路程Y(米)之间的函数关系式为 。
y=2000-200x
1、一次函数的定义
形如y=kx+b(k,b是常数,k≠0)的函数,叫做x的一次函数。
y=kx+b(k≠0)
当b=0时,一次函数y=kx(k≠0)也叫正比例函数,k叫做比例系数
新知探究:
b=0
y=kx(k≠0)
思考:当b=0时,观察一次函数y=kx+b会有什么变化?
思考:正比例函数一定是一次函数吗?一次函数一定是正比例函数吗?
一般形式 结构特征 关系
一次函数 y=kx+b(k,b为常数,且k≠0) k≠0,x的次数为1,常数项b可以是任意实数 正比例函数是一次函数的特例,一次函数包括正比例函数,即对于一次函数y=kx+b(k,b为常数,且k≠0),当b=0时,它是特殊的一次函数,即正比例函数;当b≠0时,它是一般的一次函数。
正比例函数 y=kx(k为常数,且k≠0),k叫做比例系数 k≠0,x的次数为1,常数项b=0
一次函数与正比例函数的区别与联系
一
次
函
数
正
比
例
函
数
当堂练习:下列函数中,哪些是一次函数,哪些是正比例函数?
是一次函数,也是正比例函数。
是一次函数,不是正比例函数。
不是一次函数,也不是正比例函数。
是一次函数,不是正比例函数。
不是一次函数,也不是正比例函数
是一次函数,不是正比例函数。
2、要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
3.已知下列函数:y=2x+1,s=60t,y=100-25x, , ,其中表示一次函数的有 个
4、下列说法不正确的是 ( )
A、一次函数不一定是正比例函数 B、不是一次函数就一定不是正比例函数
C、正比例函数是特定的一次函数 D、不是正比例函数就不是一次函数
4
D
题型一 利用一次函数的概念求字母的值
1、y=(m-2)xn-1+n是关于x的一次函数,m、n应满足 。
2、函数y=(2-m)x+2m-3,当m= 时,此函数为正比例函数,当m 时,此函数为一次函数
≠2
m≠2且n=3
新知探究:
思考 已知一次函数的图象经过点(3,5)与(-4,-9),如何求这个一次函数的解析式呢?
解:设这个一次函数的解析式为y=kx+b
∵y=kx+b的图象过点(3,5)与(-4,-9)
∴ 3k+b=5
-4k+b=-9
∴这个一次函数的解析式为y=2x-1
解得 k=2
b=-1
待定系数法:通过先设出表达式中的未知系数,再根据所给条件,利用解方程或方程组确定这些未知系数。
题型二 确定一次函数的表达式
1、已知y+1与x-2成正比例,当x=3时,y=-3,求y与x的函数关系式
解:∵ y+1与x-2成正比例 ∴设这个一函数的解析式为y+1=k(x-2)
∵当x=3时,y=-3 ∴ - 3+1=k(3-2) 解得 k=-2
∴这个一次函数的解析式为y=-2x+3
2、已知函数y=kx+2,当x=2时,y值为4,求k的值。
解:把x=2,y=4代入y=kx+2 得:4=2k+2 ∴k=1
3、若一次函数的图象经过点A(2,1),B(-1,-3),C(m,3),求m的值。
例 汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围,y是x的一次函数吗
题型三 一次函数解析式的简单应用
解:由题意得,函数关系式为y=50-5t,自变量x的取值范围是0≤t≤10,所以,y是x的一次函数
对于日常生活中的实际问题,解题的关键是把问题转化成数学问题,即构建相应的数学模型,建立函数关系式,通过题中条件做出答案。
我们来探究函数y=x-1的图像.
(1)给定自变量的x的一些值,求出对应y的值,并填表;
(2)以x与y的对应值作为点的坐标描出这些点;
(3)按照自变量由小到大的顺序把描出的点顺次连接起来.
如图,可得函数y=x-1的图像.
通过画图,你发现一次函数的图象是什么形状?怎样简单快速的画出一次函数的图象?
y=x-1
新知探究:
三、一次函数的图象
1、图象的形状
一次函数y=kx+b的图象是一条直线,所以也称为直线y=kx+b
2、图象的画法
一次函数的图象是一条直线,而两点确定一条直线,所以画一次函数的图象只要找出图像上的两个点,过这两个点作直线就是所求的一次函数的图象
新知探究:
练习:在同一坐标系中,画出一次函数y=2x+1与y=-2x的图象
题型三:一次函数的图象与坐标轴围成的三角形面积问题
例 已知一次函数y=kx+2的图象与x轴交于点A,与y轴交于点B,且S△OAB=3,求k的值.
课堂小结:
1、一次函数的定义
2、正比例函数是特殊的一次函数
3、对于日常生活中的实际问题,解题的关键是把问题转化成数学问题,即构建相应的数学模型,建立函数关系式,通过题中条件做出答案。
4、一次函数的图象形状与画法
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
