苏科版八年级数学下册 12.1 二次根式 课件(共16张)
文档属性
| 名称 | 苏科版八年级数学下册 12.1 二次根式 课件(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 782.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
复习回顾
1.若x2 = a(a≥0),那么x叫做a的________;
2.一个正数有____个平方根,它们___________;
3.0的平方根是____;负数___________.
4.正数a的正的平方根,叫做a的___________;记作____.
平方根
没有平方根
两
互为相反数
0
算术平方根
12.1 二次根式(1)
学习目标:
1.了解二次根式的概念,初步理解二次根式有意义的条件.
2.掌握二次根式的基本性质.
3.通过观察一些特殊的情形,获得一般的结论,感受归纳的思想方法.
重难点:
掌握二次根式的基本性质;
问题引入
S=30
问:正方形喷水池的面积为30m2,那么正方形的边长是_______m .
问题引入
问:圆形花坛的面积为S,那么这个圆的半径是_______.
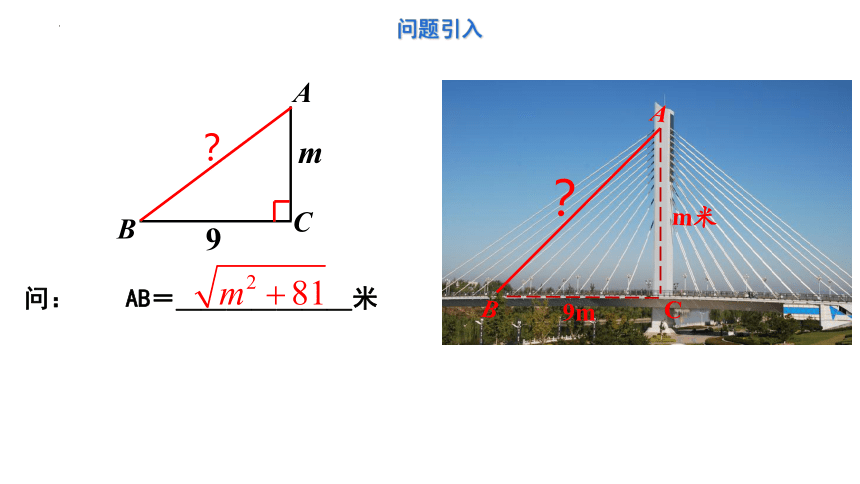
问题引入
问: AB=_______米
m米
9m
A
B
C
?
m
9
?
A
B
C
同桌讨论
、 、
你能发现它们有什么共同的特征吗
新课讲授
一.二次根式的定义:
一般地,形如 的式子叫做二次根式.
被开方数
二次根号
其中:“ ”称为二次根号;
“ a ”叫做被开方数;
、 、
独立思考:你还能举出其他的例子吗?
新课讲授
二.二次根式的判断:
(一)定义:形如 的式子叫做二次根式.
(二)特征:“ ”和“非负数a”
(三)判断方法:
二次根式
含有“ ”
被开方数a≥0
(2个条件同时满足)
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
练习巩固
独立思考:下列各式中,哪些是二次根式?哪些不是?
小组讨论
1.代数式 是二次根式吗
2.代数式 是二次根式吗
3. 、 能称为二次根式吗?
答: 代数式 只有在条件a≥0的情况下,才是二次根式;
答: 是的,(1)二次根式的被开方数可以是整式或分式.
(2)添加的x的取值范围保证了被开方数一定≥0.
答:不能,只能称为含有二次根式的代数式.
独立思考
1.当a<0时, 有意义吗?为什么?
2.当a≥0时, 可能为负数吗 为什么?
答: 无;所以 a 必须≥0;
答: 不可能;“ ”是“算数平方根”一定≥0;
所以:
“被开方数”非负(a≥0)
“二次根式”非负( ≥0)
新课讲授
二.二次根式的性质——双重非负性:
二次根式的双重非负性
二次根式的被开方数非负
二次根式的值非负
*.注意:分母中有字母时,要保证分母不为零.
(1)解:由x+1≥0,则x≥-1.
∴当x≥-1时,式子 在实数范围内有意义.
独立思考
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
∴当x为任意实数时,式子 在实数范围内有意义.
(2)解:∵在实数范围内,不论x取什么值,恒有x2 +2>0,
独立思考
(3)解:∵在实数范围内,不论x取什么值,恒有-x2≤0;
又∵二次根式的被开方数大于等于零;
∴当x=0时, 式子 在实数范围内有意义.
∴ -x2=0,即x=0;
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
独立思考
(4)解:由题目条件:
解①得:x ≤ ;
解②得:x ≠ .
∴不等式组的解集为:x< .
∴当x< 时, 式子 在实数范围内有意义.
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
新课讲授
三.一个重要公式——先开方后平方:
思考:当a≥0时, 等于什么?说说你是如何理解的.
当 时,
1.计算:
2.计算:
复习回顾
1.若x2 = a(a≥0),那么x叫做a的________;
2.一个正数有____个平方根,它们___________;
3.0的平方根是____;负数___________.
4.正数a的正的平方根,叫做a的___________;记作____.
平方根
没有平方根
两
互为相反数
0
算术平方根
12.1 二次根式(1)
学习目标:
1.了解二次根式的概念,初步理解二次根式有意义的条件.
2.掌握二次根式的基本性质.
3.通过观察一些特殊的情形,获得一般的结论,感受归纳的思想方法.
重难点:
掌握二次根式的基本性质;
问题引入
S=30
问:正方形喷水池的面积为30m2,那么正方形的边长是_______m .
问题引入
问:圆形花坛的面积为S,那么这个圆的半径是_______.
问题引入
问: AB=_______米
m米
9m
A
B
C
?
m
9
?
A
B
C
同桌讨论
、 、
你能发现它们有什么共同的特征吗
新课讲授
一.二次根式的定义:
一般地,形如 的式子叫做二次根式.
被开方数
二次根号
其中:“ ”称为二次根号;
“ a ”叫做被开方数;
、 、
独立思考:你还能举出其他的例子吗?
新课讲授
二.二次根式的判断:
(一)定义:形如 的式子叫做二次根式.
(二)特征:“ ”和“非负数a”
(三)判断方法:
二次根式
含有“ ”
被开方数a≥0
(2个条件同时满足)
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
练习巩固
独立思考:下列各式中,哪些是二次根式?哪些不是?
小组讨论
1.代数式 是二次根式吗
2.代数式 是二次根式吗
3. 、 能称为二次根式吗?
答: 代数式 只有在条件a≥0的情况下,才是二次根式;
答: 是的,(1)二次根式的被开方数可以是整式或分式.
(2)添加的x的取值范围保证了被开方数一定≥0.
答:不能,只能称为含有二次根式的代数式.
独立思考
1.当a<0时, 有意义吗?为什么?
2.当a≥0时, 可能为负数吗 为什么?
答: 无;所以 a 必须≥0;
答: 不可能;“ ”是“算数平方根”一定≥0;
所以:
“被开方数”非负(a≥0)
“二次根式”非负( ≥0)
新课讲授
二.二次根式的性质——双重非负性:
二次根式的双重非负性
二次根式的被开方数非负
二次根式的值非负
*.注意:分母中有字母时,要保证分母不为零.
(1)解:由x+1≥0,则x≥-1.
∴当x≥-1时,式子 在实数范围内有意义.
独立思考
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
∴当x为任意实数时,式子 在实数范围内有意义.
(2)解:∵在实数范围内,不论x取什么值,恒有x2 +2>0,
独立思考
(3)解:∵在实数范围内,不论x取什么值,恒有-x2≤0;
又∵二次根式的被开方数大于等于零;
∴当x=0时, 式子 在实数范围内有意义.
∴ -x2=0,即x=0;
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
独立思考
(4)解:由题目条件:
解①得:x ≤ ;
解②得:x ≠ .
∴不等式组的解集为:x< .
∴当x< 时, 式子 在实数范围内有意义.
问:x是怎样的实数时,下列式子在实数范围内有意义?
(3) ; (4) .
(1) ; (2) ;
新课讲授
三.一个重要公式——先开方后平方:
思考:当a≥0时, 等于什么?说说你是如何理解的.
当 时,
1.计算:
2.计算:
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
