青岛版七年级数学下册 12.1平方差公式 课件(共16张)
文档属性
| 名称 | 青岛版七年级数学下册 12.1平方差公式 课件(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 836.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 21:15:53 | ||
图片预览




文档简介
(共16张PPT)
12.1平方差公式
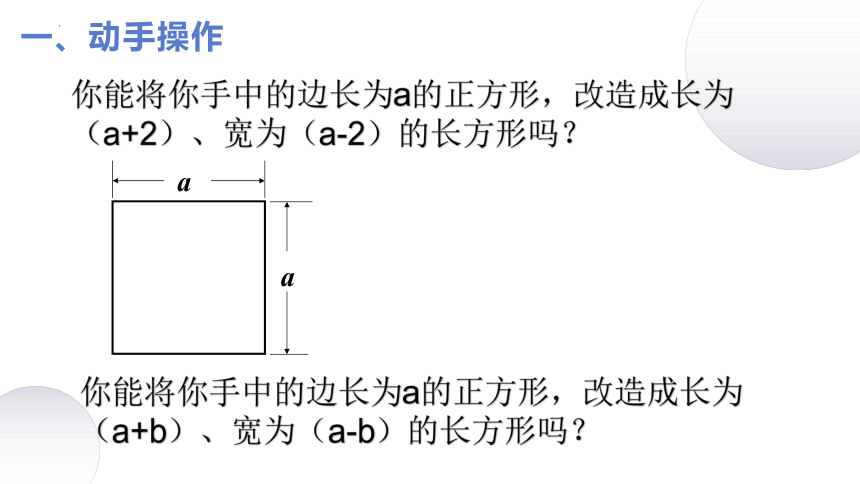
一、动手操作
你能将你手中的边长为a的正方形,改造成长为(a+2)、宽为(a-2)的长方形吗?
a
a
你能将你手中的边长为a的正方形,改造成长为(a+b)、宽为(a-b)的长方形吗?
a
a
a
b
a-b
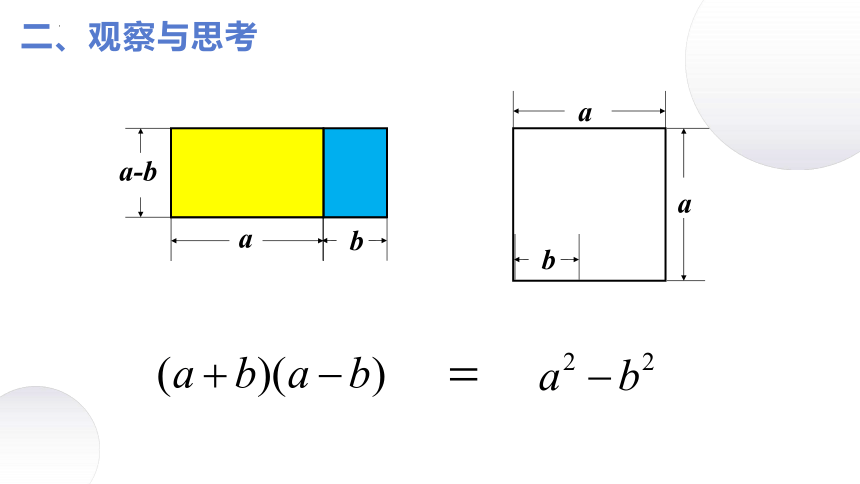
二、观察与思考
b
(a+b)(a-b)
证明:
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
=a2-ab+ab-b2
=a2-b2
验证
三、理论验证
平方差公式
(a+b)(a b)=
a2 b2
两个数的和与这两个数的差的乘积,等于这两个数的平方差
成果
:1、平方差公式有什么结构特征?
(a+b)(a b)=
a2 b2
2、在使用这个公式时应该注意什么?
想一想
左边:
(1)两个二项式相乘
(2)有一项相同,另一项互为相反项
右边:
相同的平方减去相反项的平方
找清哪个是相同的,即公式中的a,
哪个是互为相反的,即公式中的b
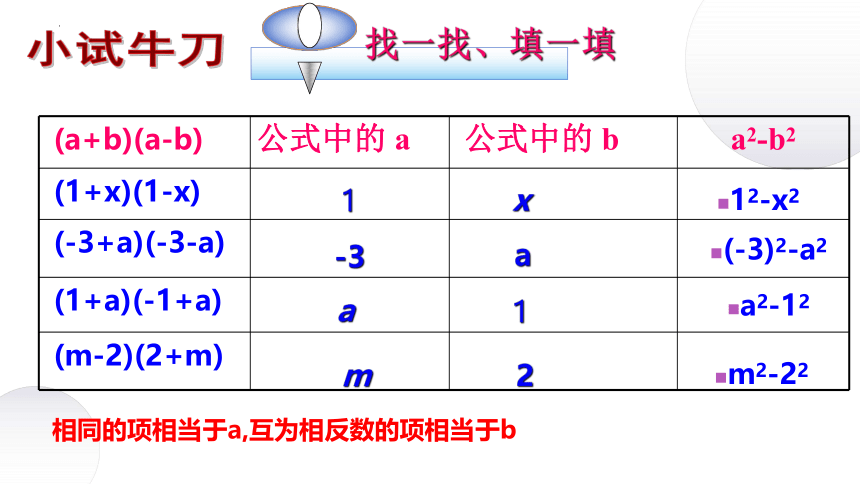
找一找、填一填
(a+b)(a-b) 公式中的 a 公式中的 b a2-b2
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(m-2)(2+m)
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
m
2
m2-22
小试牛刀
相同的项相当于a,互为相反数的项相当于b
例1、运用平方差公式计算下列各题:
谁相当于公式中的a
谁相当于公式中的b
=49-4m4
=(3x)2-(2y)2
=9x2-4y2
=(-7)2-(2m2)2
(1)(3x+2y) (3x-2y)
(2)(-7+2m2) (-7-2m2)
四、公式应用
(3)(x+1)(x-1)(x2+1)
=(x2-1) (x2+1)
=x4-1
谁相当于公式中的a
谁相当于公式中的b
五、当堂练习——课本P111 练习1
a2-36
1-x2
x2-400y2
a4-81
例2、运用平方差公式简便计算:
=(800+3) (800-3)
=8002-32
=640000-9
=639991
803 797
五、当堂练习——课本P112 第2题
2、(1)73×67 (2)99.8×100.2
=(70+3)(70-3)
=702—32
=4891
=(100-0.2)(100+0.2)
=1002-0.22
=9999.96
六、挑战自我P111
六、当堂练习——拓展P112第6题
1、下列多项式乘法中能用平方差公式
计算的是( ).
(A)(x+1)(1+x) (B)(2x+y)(-y-2x)
(C)(-m+n)(-m-n) (D)(x2-y)(x+y2)
2、填空(1)(x2-2)(x2+2)= ( )
(2)(5x-3y)( )=25x2-9y2
3、利用平方差公式计算:
(1)(-2x+3y)(-2x-3y)
(2) 98×102
C
X4-4
5X+3y
4x2-9y2
9996
(3)(a+2)(a-2)(a2+4)
a4-16
当堂检测
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
小结
12.1平方差公式
一、动手操作
你能将你手中的边长为a的正方形,改造成长为(a+2)、宽为(a-2)的长方形吗?
a
a
你能将你手中的边长为a的正方形,改造成长为(a+b)、宽为(a-b)的长方形吗?
a
a
a
b
a-b
二、观察与思考
b
(a+b)(a-b)
证明:
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
=a2-ab+ab-b2
=a2-b2
验证
三、理论验证
平方差公式
(a+b)(a b)=
a2 b2
两个数的和与这两个数的差的乘积,等于这两个数的平方差
成果
:1、平方差公式有什么结构特征?
(a+b)(a b)=
a2 b2
2、在使用这个公式时应该注意什么?
想一想
左边:
(1)两个二项式相乘
(2)有一项相同,另一项互为相反项
右边:
相同的平方减去相反项的平方
找清哪个是相同的,即公式中的a,
哪个是互为相反的,即公式中的b
找一找、填一填
(a+b)(a-b) 公式中的 a 公式中的 b a2-b2
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(m-2)(2+m)
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
m
2
m2-22
小试牛刀
相同的项相当于a,互为相反数的项相当于b
例1、运用平方差公式计算下列各题:
谁相当于公式中的a
谁相当于公式中的b
=49-4m4
=(3x)2-(2y)2
=9x2-4y2
=(-7)2-(2m2)2
(1)(3x+2y) (3x-2y)
(2)(-7+2m2) (-7-2m2)
四、公式应用
(3)(x+1)(x-1)(x2+1)
=(x2-1) (x2+1)
=x4-1
谁相当于公式中的a
谁相当于公式中的b
五、当堂练习——课本P111 练习1
a2-36
1-x2
x2-400y2
a4-81
例2、运用平方差公式简便计算:
=(800+3) (800-3)
=8002-32
=640000-9
=639991
803 797
五、当堂练习——课本P112 第2题
2、(1)73×67 (2)99.8×100.2
=(70+3)(70-3)
=702—32
=4891
=(100-0.2)(100+0.2)
=1002-0.22
=9999.96
六、挑战自我P111
六、当堂练习——拓展P112第6题
1、下列多项式乘法中能用平方差公式
计算的是( ).
(A)(x+1)(1+x) (B)(2x+y)(-y-2x)
(C)(-m+n)(-m-n) (D)(x2-y)(x+y2)
2、填空(1)(x2-2)(x2+2)= ( )
(2)(5x-3y)( )=25x2-9y2
3、利用平方差公式计算:
(1)(-2x+3y)(-2x-3y)
(2) 98×102
C
X4-4
5X+3y
4x2-9y2
9996
(3)(a+2)(a-2)(a2+4)
a4-16
当堂检测
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
小结
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
