19-1-2函数的图像(第2课时)课件人教版数学八年级下册(30张ppt)
文档属性
| 名称 | 19-1-2函数的图像(第2课时)课件人教版数学八年级下册(30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 21:23:44 | ||
图片预览







文档简介
(共30张PPT)
人教版 八年级数学下
19.1.2 函数的图象
第2课时 函数的表示方法
第十九章 一次函数
时间:2022/5/9
知识回顾
1.函数的图象 一般的,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
2.描点法画函数图像的一般步骤
1
列表:表中给出一些自变量的值及其对应的函数值.
2
描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点.
3
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.
1.全面理解函数的三种表示方法.
2.会从实际问题的图象中读取信息.
学习目标
练习
解:(1)列表
根据表中数值描点(x,y) ,并用平滑的曲线连接这些点.
p79
1.(1)画出函数 y = 2x-1 的图象;
(2)判断点A(-2.5, -4), B(1, 3), C(2.5, 4)是否在此函数的图象上.
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
练习
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
1.(1)画出函数 y = 2x-1 的图象;
(2)判断点A(-2.5, -4), B(1, 3), C(2.5, 4)是否在此函数的图象上.
p79
3
2
知识精讲
函数的三种表示法:
y = 2x-1
图象法.
列表法、
解析式法、
函数的三种表示方法
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
3
2
新知探究
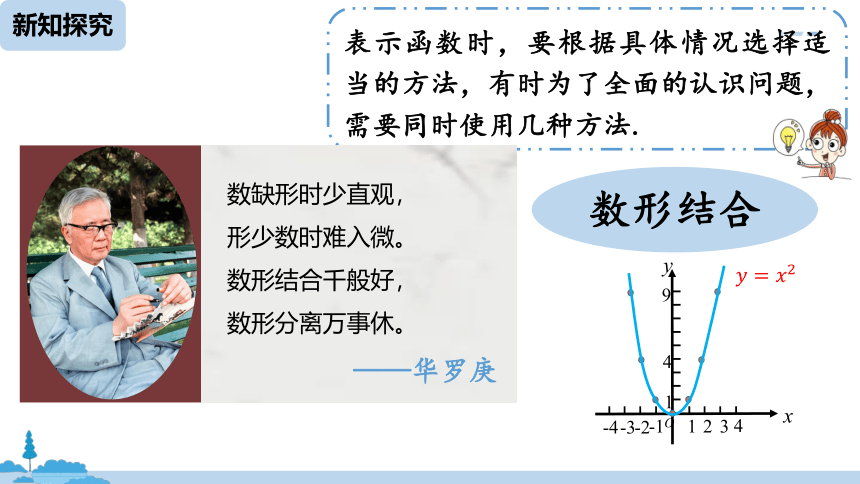
表示函数时,要根据具体情况选择适当的方法,有时为了全面的认识问题,需要同时使用几种方法.
数形结合
O
1
2
3
4
1
4
9
-4
-3
-2
-1
x
y
数缺形时少直观,
形少数时难入微。
数形结合千般好,
数形分离万事休。
——华罗庚
新知探究
这三种表示函数的方法各有什么优点?
2.列表法:具体地反映函数与自变量的数值对应关系.
3.图象法:直观、形象地反映出函数的变化趋势和性质.
1.解析式法:简单明了,能够准确的反映整个变化过程中自变量与函数之间的对应关系.
y = 2x-1
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
t/时
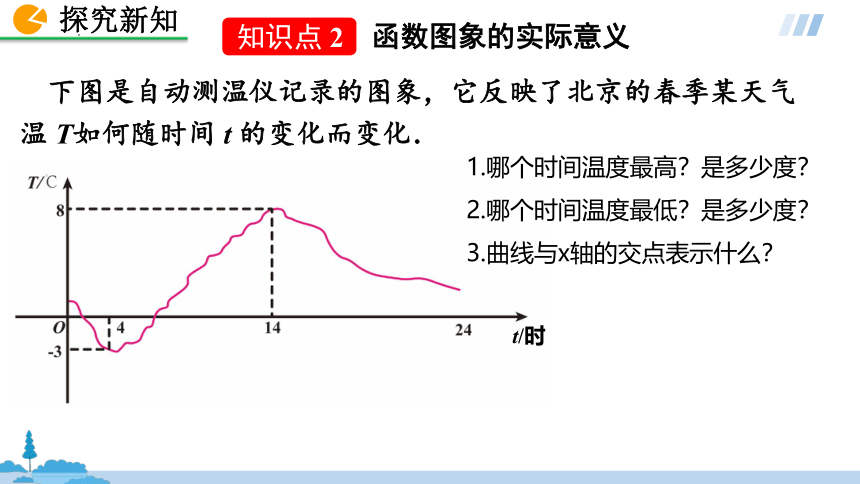
下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T如何随时间 t 的变化而变化.
探究新知
知识点 2
函数图象的实际意义
1.哪个时间温度最高?是多少度?
2.哪个时间温度最低?是多少度?
3.曲线与x轴的交点表示什么?
t/时
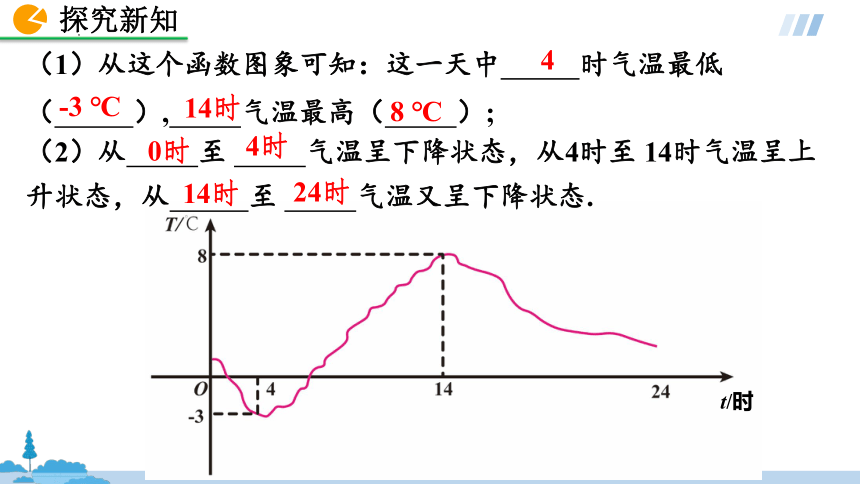
(1)从这个函数图象可知:这一天中 时气温最低( ), 气温最高( );
4
-3 ℃
14时
8 ℃
(2)从 至 气温呈下降状态,从4时至 14时气温呈上升状态,从 至 气温又呈下降状态.
0时
4时
14时
24时
探究新知
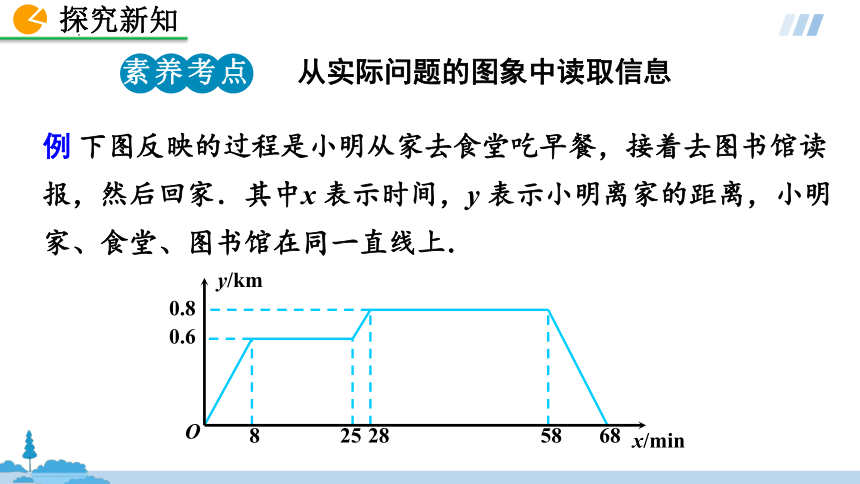
例 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
探究新知
素养考点 1
从实际问题的图象中读取信息
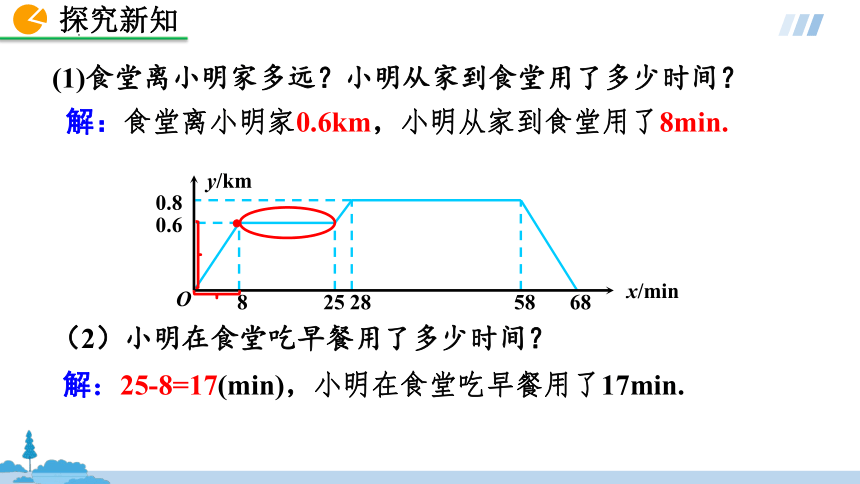
(2)小明在食堂吃早餐用了多少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:25-8=17(min),小明在食堂吃早餐用了17min.
探究新知
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:食堂离小明家0.6km,小明从家到食堂用了8min.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
解:0.8-0.6=0.2(km),食堂离图书馆0.2km;
探究新知
28-25=3(min),小明从食堂到图书馆用了3min.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多长时间?
解:58-28=30(min),小明读报用了30min.
探究新知
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:图书馆离小明家0.8km,小明从图书馆回家用了68-58=10(min),由此算出的平均速度是0.08km/min.
探究新知
探究新知
方法点拨
解答图象信息题主要运用数形结合思想,把图象信息转化为数字信息.
主要步骤如下:
(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?
答:7时 和 12时.
答:在0时— 7时和12时— 24时比北京气温高;
在7时—12时比北京气温低.
2.如图是某一天北京与上海的气温随时间变化的图象.
根据图像回答下列问题.
练习
p79
新知探究
例4 一个水库的水位在最近5h内持续上涨,下表记录了这5h内 6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
解:如图,描出表中数据对应的点.可以看出,这6个点在一条直线上.
解:可以看出,这6个点 ,且每小时水位上升 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
0.3m
探究新知
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出符合表中数据的函数解析式,并画出函数图象. 这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
y=0.3t+3
(3)据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米?
解:(3)如果水位的变化规律不变,则可利用上述函数预测,再过 2 h,即 t=5+2=7(h) 时,水位高度y=0.3×7+3=5.1(m).
新知探究
或把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,从图象也能看出这时的水位高度约为 5.1 m.
课堂小结
1.函数的三种表示法:
y = 2x-1
图象法.
列表法、
解析式法、
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
3
2
2.函数图象的实际意义
1.最近中旗连降雨雪,德岭山水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
基础巩固题
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
答:体育场离张强家2.5千米.
张强从家到体育场用15分钟.
4.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
课堂检测
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)张强从文具店回家的平均速度是多少?
解:2.5-1.5=1(千米),体育场离文具店1千米.
解:65-45=20(分),张强在文具店停留了20分钟.
课堂检测
解:依题意可得
1.5÷[(100-65)÷60]
拓展提升
3.(1)画出函数的图象.
(2)从图象中观察,当 x<0 时,y 随 x 的增大而增大,还是 y 随 x 的增大而减小?当 x>0 时呢?
解:(1)列表:
x …… -3 -2 -1 0 1 2 3 ……
y …… 9 4 1 0 1 4 9 ……
练习
p79
描点、连线,所画图象如图所示:
(2)从图象中观察,
当 x<0 时,y随 x 的增大而减小. 当 x>0 时,y 随 x 的增大而增大.
O
1
2
3
4
1
4
9
-4
-3
-2
-1
x
y
练习
甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;
②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是( )
A.①②③ B.①②④
C.①③④ D.①②③④
A
连接中考
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
课堂检测
能力提升题
①
②
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
人教版 八年级数学下
19.1.2 函数的图象
第2课时 函数的表示方法
第十九章 一次函数
时间:2022/5/9
知识回顾
1.函数的图象 一般的,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
2.描点法画函数图像的一般步骤
1
列表:表中给出一些自变量的值及其对应的函数值.
2
描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点.
3
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑的曲线连接起来.
1.全面理解函数的三种表示方法.
2.会从实际问题的图象中读取信息.
学习目标
练习
解:(1)列表
根据表中数值描点(x,y) ,并用平滑的曲线连接这些点.
p79
1.(1)画出函数 y = 2x-1 的图象;
(2)判断点A(-2.5, -4), B(1, 3), C(2.5, 4)是否在此函数的图象上.
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
练习
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
1.(1)画出函数 y = 2x-1 的图象;
(2)判断点A(-2.5, -4), B(1, 3), C(2.5, 4)是否在此函数的图象上.
p79
3
2
知识精讲
函数的三种表示法:
y = 2x-1
图象法.
列表法、
解析式法、
函数的三种表示方法
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
3
2
新知探究
表示函数时,要根据具体情况选择适当的方法,有时为了全面的认识问题,需要同时使用几种方法.
数形结合
O
1
2
3
4
1
4
9
-4
-3
-2
-1
x
y
数缺形时少直观,
形少数时难入微。
数形结合千般好,
数形分离万事休。
——华罗庚
新知探究
这三种表示函数的方法各有什么优点?
2.列表法:具体地反映函数与自变量的数值对应关系.
3.图象法:直观、形象地反映出函数的变化趋势和性质.
1.解析式法:简单明了,能够准确的反映整个变化过程中自变量与函数之间的对应关系.
y = 2x-1
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
t/时
下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T如何随时间 t 的变化而变化.
探究新知
知识点 2
函数图象的实际意义
1.哪个时间温度最高?是多少度?
2.哪个时间温度最低?是多少度?
3.曲线与x轴的交点表示什么?
t/时
(1)从这个函数图象可知:这一天中 时气温最低( ), 气温最高( );
4
-3 ℃
14时
8 ℃
(2)从 至 气温呈下降状态,从4时至 14时气温呈上升状态,从 至 气温又呈下降状态.
0时
4时
14时
24时
探究新知
例 下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
探究新知
素养考点 1
从实际问题的图象中读取信息
(2)小明在食堂吃早餐用了多少时间?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:25-8=17(min),小明在食堂吃早餐用了17min.
探究新知
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
解:食堂离小明家0.6km,小明从家到食堂用了8min.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
解:0.8-0.6=0.2(km),食堂离图书馆0.2km;
探究新知
28-25=3(min),小明从食堂到图书馆用了3min.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多长时间?
解:58-28=30(min),小明读报用了30min.
探究新知
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:图书馆离小明家0.8km,小明从图书馆回家用了68-58=10(min),由此算出的平均速度是0.08km/min.
探究新知
探究新知
方法点拨
解答图象信息题主要运用数形结合思想,把图象信息转化为数字信息.
主要步骤如下:
(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?
答:7时 和 12时.
答:在0时— 7时和12时— 24时比北京气温高;
在7时—12时比北京气温低.
2.如图是某一天北京与上海的气温随时间变化的图象.
根据图像回答下列问题.
练习
p79
新知探究
例4 一个水库的水位在最近5h内持续上涨,下表记录了这5h内 6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
解:如图,描出表中数据对应的点.可以看出,这6个点在一条直线上.
解:可以看出,这6个点 ,且每小时水位上升 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
0.3m
探究新知
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出符合表中数据的函数解析式,并画出函数图象. 这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
y=0.3t+3
(3)据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米?
解:(3)如果水位的变化规律不变,则可利用上述函数预测,再过 2 h,即 t=5+2=7(h) 时,水位高度y=0.3×7+3=5.1(m).
新知探究
或把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,从图象也能看出这时的水位高度约为 5.1 m.
课堂小结
1.函数的三种表示法:
y = 2x-1
图象法.
列表法、
解析式法、
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
O
1
2
3
4
1
4
-3
-2
-1
x
y
-3
3
2
2.函数图象的实际意义
1.最近中旗连降雨雪,德岭山水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
基础巩固题
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
答:体育场离张强家2.5千米.
张强从家到体育场用15分钟.
4.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
课堂检测
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)张强从文具店回家的平均速度是多少?
解:2.5-1.5=1(千米),体育场离文具店1千米.
解:65-45=20(分),张强在文具店停留了20分钟.
课堂检测
解:依题意可得
1.5÷[(100-65)÷60]
拓展提升
3.(1)画出函数的图象.
(2)从图象中观察,当 x<0 时,y 随 x 的增大而增大,还是 y 随 x 的增大而减小?当 x>0 时呢?
解:(1)列表:
x …… -3 -2 -1 0 1 2 3 ……
y …… 9 4 1 0 1 4 9 ……
练习
p79
描点、连线,所画图象如图所示:
(2)从图象中观察,
当 x<0 时,y随 x 的增大而减小. 当 x>0 时,y 随 x 的增大而增大.
O
1
2
3
4
1
4
9
-4
-3
-2
-1
x
y
练习
甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;
②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是( )
A.①②③ B.①②④
C.①③④ D.①②③④
A
连接中考
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
课堂检测
能力提升题
①
②
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
