19-2-1菱形的性质课件-华东师大版八年级数学下册(17张ppt)
文档属性
| 名称 | 19-2-1菱形的性质课件-华东师大版八年级数学下册(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 990.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
19.2.1 菱形的性质
复习回顾
我知道的四边形、平行四边形、矩形是怎么样的呢?
四边形
平行四边形
有一个角是直角
矩形
思考:如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?
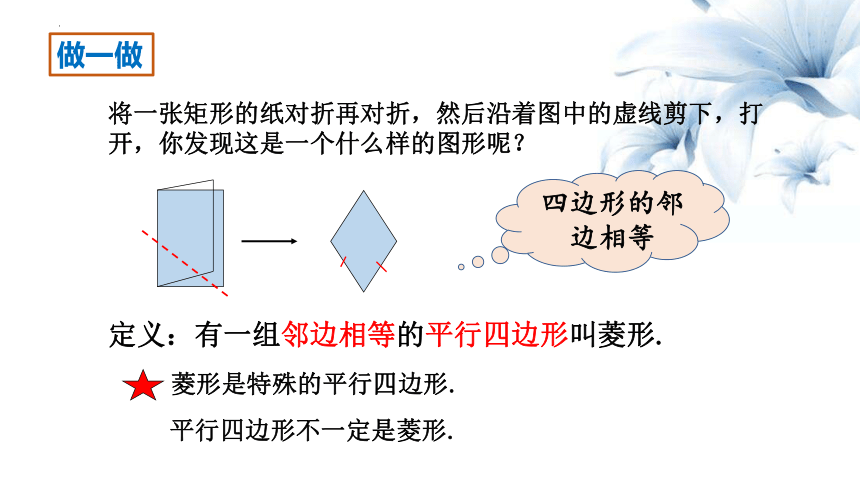
做一做
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
定义:有一组邻边相等的平行四边形叫菱形.
四边形的邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
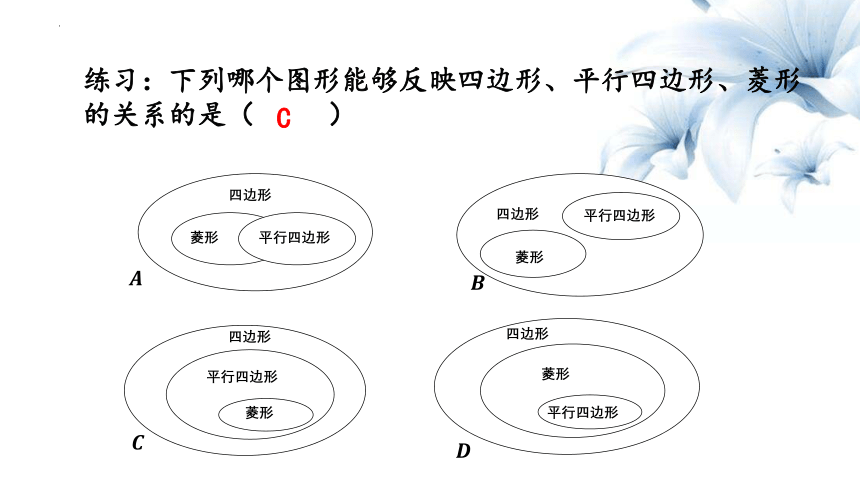
练习:下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
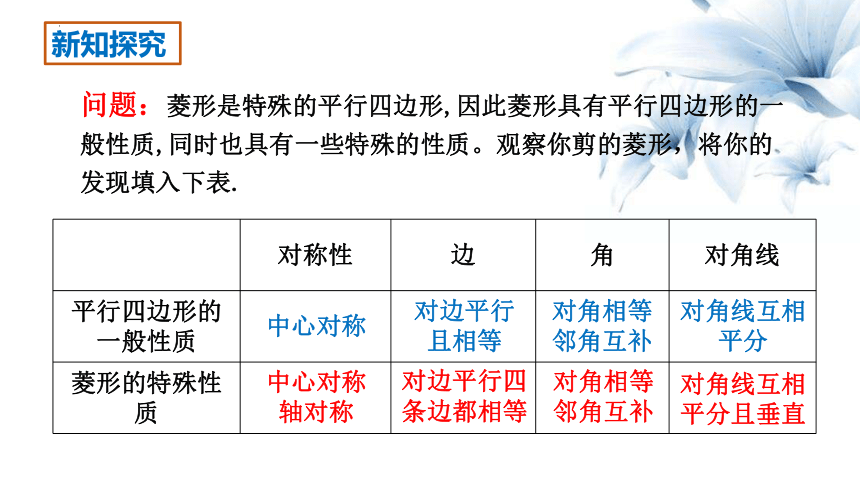
新知探究
问题:菱形是特殊的平行四边形,因此菱形具有平行四边形的一般性质,同时也具有一些特殊的性质。观察你剪的菱形,将你的发现填入下表.
对称性 边 角 对角线
平行四边形的 一般性质
菱形的特殊性质
中心对称
轴对称
中心对称
对边平行且相等
对边平行四条边都相等
对角相等
邻角互补
对角相等
邻角互补
对角线互相平分
对角线互相平分且垂直
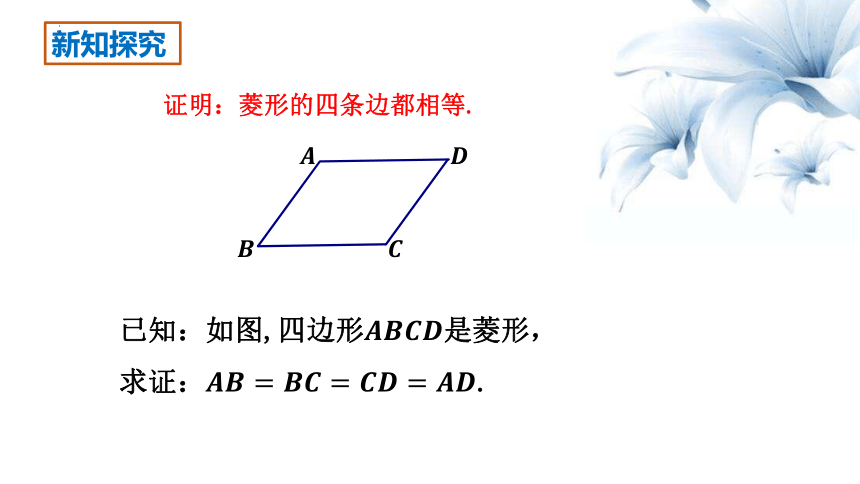
新知探究
证明:菱形的四条边都相等.
已知:如图,四边形是菱形,
求证:.
新知概括
菱形的性质定理1:菱形的四条边都相等.
应用格式:
∵四边形是菱形
∴
例1、如图,在菱形中,. 试求出的大小,并说明是等边三角形.
新知探究
证明:菱形的对角线互相垂直.
已知:如图,四边形是菱形,
求证:.
新知概括
菱形的性质定理2:菱形的对角线互相垂直.
应用格式:
∵四边形是菱形
∴
例2、如图,已知菱形的边长为,,对角线、相交于点.试求这个菱形的两条对角线与的长. (结果保留根号)
例3、如图,菱形的对角线与相交于点,垂直且平分,垂足为点.求的大小.
1、如图,在菱形中,,,则的周长等于( )
A.18 B.16 C.15 D.14
B
2、如图,菱形中,,若的周长为15,则菱形的周长是( )
A.25 B.20 C.15 D.10
B
3、如图,已知菱形的边长为,其中对角线长.
求:(1)对角线的长度; (2)菱形的面积.
D
B
C
A
E
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
1.如图,菱形的顶点在轴上,顶点的坐标为,若反比例函数的图象经过点.
(1)求点的坐标;
(2)求的值.
能力提升
2.如图,点是菱形对角线的交点,//,//,连结
(1)求证:;
(2)若四边形的面积是8,求菱形的面积.
19.2.1 菱形的性质
复习回顾
我知道的四边形、平行四边形、矩形是怎么样的呢?
四边形
平行四边形
有一个角是直角
矩形
思考:如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?
做一做
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
定义:有一组邻边相等的平行四边形叫菱形.
四边形的邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
练习:下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
新知探究
问题:菱形是特殊的平行四边形,因此菱形具有平行四边形的一般性质,同时也具有一些特殊的性质。观察你剪的菱形,将你的发现填入下表.
对称性 边 角 对角线
平行四边形的 一般性质
菱形的特殊性质
中心对称
轴对称
中心对称
对边平行且相等
对边平行四条边都相等
对角相等
邻角互补
对角相等
邻角互补
对角线互相平分
对角线互相平分且垂直
新知探究
证明:菱形的四条边都相等.
已知:如图,四边形是菱形,
求证:.
新知概括
菱形的性质定理1:菱形的四条边都相等.
应用格式:
∵四边形是菱形
∴
例1、如图,在菱形中,. 试求出的大小,并说明是等边三角形.
新知探究
证明:菱形的对角线互相垂直.
已知:如图,四边形是菱形,
求证:.
新知概括
菱形的性质定理2:菱形的对角线互相垂直.
应用格式:
∵四边形是菱形
∴
例2、如图,已知菱形的边长为,,对角线、相交于点.试求这个菱形的两条对角线与的长. (结果保留根号)
例3、如图,菱形的对角线与相交于点,垂直且平分,垂足为点.求的大小.
1、如图,在菱形中,,,则的周长等于( )
A.18 B.16 C.15 D.14
B
2、如图,菱形中,,若的周长为15,则菱形的周长是( )
A.25 B.20 C.15 D.10
B
3、如图,已知菱形的边长为,其中对角线长.
求:(1)对角线的长度; (2)菱形的面积.
D
B
C
A
E
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
1.如图,菱形的顶点在轴上,顶点的坐标为,若反比例函数的图象经过点.
(1)求点的坐标;
(2)求的值.
能力提升
2.如图,点是菱形对角线的交点,//,//,连结
(1)求证:;
(2)若四边形的面积是8,求菱形的面积.
