19-2-3一次函数与二元一次方程(组)课件--人教版八年级数学下册(42张ppt)
文档属性
| 名称 | 19-2-3一次函数与二元一次方程(组)课件--人教版八年级数学下册(42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 410.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 21:32:54 | ||
图片预览










文档简介
(共42张PPT)
19.2 一次函数
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第2课时
一次函数与二元一次方程(组)
导入新课
观察与思考
今天数学王国建了两个健身团,各个成员要按照
自己所在的集合加入对应粉丝团,这时来了“x+y=5”.
到我这里来
欢迎
加入
这是怎么回事?到底应该加到哪呢?
欢迎
加入
二元一
次方程
一次函数
二元一次方程与一次函数解析式的关系
数学活动一、
探究新知
1. 你能把二元一次方程x+y=5 改写成y= 的形式吗?
问题
5-x
2. 一次函数y=-x+5也可以通过变形得到相应的二元一次
方程ax+by=c的形式吗?
3. 任意的二元一次方程与对应的一次函数解析式都可以进行这样的转化吗?
总结:
每个二元一次方程都对应一个一次函数解析式,
每个一次函数解析式也对应着一个二元一次方程.
即二元一次方程与对应的一次函数解析式可以互相
转化.
一次函数图象上的点与二元一次方程的解的关系
数学活动二、
1. 二元一次方程x+y=5 的解有多少个?请你写出方程的
几个解,把以这几个解为坐标的点在坐标系中描出来.
问题
无数个解
…
O
x
y
1
1
y =-x+5
x … -1 0 1 2 3 4 5 …
y … 6 5 4 3 2 1 0 …
2. 如果再给出一些以方程的解为坐标的点,你能发现什么规律吗?
3. 这些点是否在某个一次函数图象上?为什么?
4. 反之,在一次函数y = -x + 5图象上任取一点,它的坐标适合方程x + y =5吗?
这些点在一条直线上.
在一次函数y=-x+5的图象上.
总结:
以二元一次方程的解为坐标的点都在相应的一次
函数图象上;一次函数图象上的点的坐标都适合相应
的二元一次方程.
二元一次方程组(的解)与一次函数(图象的交点)的关系
数学活动三、
1. 在同一坐标系中分别画出一次函数y=2x-1与y=5-x的图象,这两个图象有交点吗?
问题
x 5 0
y=5-x 0 5
x 1 0
y=2x -1 1 -1
(1)列表:
(2)描点;
O
x
y
1
1
y =-x+5
(2,3)
(3)连线;
y=2x-1
由方程组
y =-x+5,
y =2x-1,
解得
x =2,
y =3.
2. 交点坐标与二元一次方程组 的解有什么
关系?
y =-x+5,
y =2x-1,
方程组的解就是使方程组中两个方程同时成立的解,而这一对未知数也同时满足两个相应的一次函数解析式,因此方程组的解就是两个相应的一次函数图象的交点坐标.
3. 求二元一次方程组 的解,你有哪些方法?
x - y =-4,
2x+y =1,
加减消元法,
代入消元法,
图象法.
下面我们用图象法求解.
O
x
y
y =-2x+1
1
1
解:
由题可得:y =-2x+1和y =x+4.
在同一坐标系中画出两个一次函数图象如下:
y =x+4
两个一次函数图象
的交点为(-1,3).
(-1,3)
所以原二元一次方程组的解为
x =-1,
y =3.
但是由于画图的不准确性,
所求的解往往是近似解,
导致图象解法有一定的局限性.
用图象法求二元一次方程组的解的一般步骤:
(1)变函数:把方程组化为一次函数;
(2)画图象:
建立平面直角坐标系,画出两个一次函数的图象;
(3)找交点:由图象确定两条直线交点的坐标;
(4)写结论:依据交点的坐标写出方程组的解.
4.一次函数图象是直线,那么直线一定是一次函数吗?
不一定是一次函数.
如,直线x=2,直线y=-1等.
5.什么是二元一次方程组?
x =-1,
y =3,
是二元一次方程组吗?
x =-1,
y =3,
6. 二元一次方程组 的解是什么?
还能用图象法求该方程组的解吗?
O
x
y
1
1
x =-1
y =3
(-1,3)
1.一次函数图象是直线,但直线不一定是一次函数;
总结:
2.二元一次方程组对应两条直线,但不一定对应两个
一次函数.
4.一般地,从图形角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定两条直线交点的坐标.
3.由于图象解法的局限性.因此为了准确地解决有关图象
问题常常把它转化为代数问题来处理.
应用二元一次方程与一次函数的关系解决问题
数学活动四、
如图,直线y=k x + b与y=m x + n交于点(1,3),则
方程组 的解为 .
问题
O
x
y
y =kx+b
y =mx+n
1
1
y=k x + b
y=m x + n
x =1
y =3
(1,3)
如图,直线y=k x + b与y=m x + n交于点(1,3),则
方程组 的解为 .
变式:
O
x
y
y =kx+b
y =mx+n
1
1
y=-k x + b
y=-m x + n
x =-1
y =3
y=-k x + b
y=-m x + n
y=k(- x )+ b
y=m(- x )+ n
(1,3)
(-1,3)
二元一次方程组的解的三种情况
数学活动五、
问题
1. 二元一次方程组的解有哪些情况?
通过求下列二元一次方程组的解回忆一下.
无解
x =-1,
y =3;
x-y =-4;
2x+y =1,
①
x + y =2;
x + y =1,
②
2x +2y =2.
x + y =1,
③
无数个解
唯一解
2. 你能用画图象的方法求出以上二元一次方程组的解吗?
y =x+4
y =-2x+1
O
x
y
1
1
① y =-2x+1和y =x+4;
(-1,3)
k值不相等,两条直线不平行(相交),
有一个交点,对应方程组有唯一解.
y =-x+2
y =-x+1
O
x
y
1
1
② y =-x+1和y =-x+2;
k值相等,且b值不相等,两条直线平行,
无公共点,对应方程组无解.
y =-x+1
O
x
y
1
1
③ y =-x+1和y =-x+1.
k、b值均相等,两直线重合,
有无数个公共点,对应方程组无数个解.
由此,你发现了什么?
二元一次方程组
的解的个数
总结:
一次函数图象
的交点个数
唯一解
图象相交(有一个交点)
无解
图象平行(无交点)
无数个解
图象重合(有无数个交点)
检测反馈
B
2x +2y =3,
x + y =2,
1.若方程组 没有解,则一次函数
y=2-x和y= - x的图象必定( )
A.重合 B.平行 C.相交 D.无法确定
B
a2x -y =-b2,
a1x + y =b1,
2.直线y=-a1x+b1与直线y=a2x+b2若有唯一交点,则
二元一次方程组 的解的情况是( )
A.无解 B.有唯一解
C.有两组解 D.有无数组解
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
1号探测气球海拔高度:y =x+5( 0≤ x≤60 );
(1)用式子分别表示两个气球所在位置的海拔 y
(单位:m)关于上升时间 x(单位:min)
的函数关系.
2号探测气球海拔高度:y =0.5x+15 ( 0≤ x≤60 ) .
学以致用
(1)解:
答:当上升20min时,两个气球都位于海拔25m的高度 .
(2)由方程组
y =x+5,
(2)在某时刻,两个能否位于同一高度?这时的高度
是多少?如果能,这时气球上升了多长时间?位
于什么高度?
y =0.5x+15,
解得
x =20,
y =25.
两个图象的交点坐标为(20,25),这也说明当上升20min时,两个气球都位于海拔25m的高度 .
(20,25)
y =x+5 ( 0≤ x≤60 )
y =0.5x+15 ( 0≤ x≤60 )
10
40
O
x/min
y/m
10
30
20
20
30
40
我们也可以用一次函数的图象解释上述问题的解答.
50
60
50
60
两个图象
的交点坐
标为(20,25),
这也说明
当上20min
时,两个
气球都位
于海拔25
m的高度 .
素养提升
如图,直线l1:y=x+1与直线l2 :y=mx+n相交于点P(2,b).
(1)求b的值;
解:(1)把(2,b)代入y=x+1中,得b=2+1,
∴ b=3.
(2)直接写出方程组 的解;
mx-y +n=0
x-y+1 =0
(2)方程组的解为
x =2,
y =3.
l2
l1
O
x
y
b
2
A
B
P
(3)
m =-1,
n =5.
l2
l1
O
x
y
b
2
A
B
P
(3)若l1交x轴于点A, l2交x轴于点B,且
求l2对应的解析式.
∴ AB=6.
∵直线l1:y=x+1中,y=0时,x=-1.
∴ OA=1.
∴ OB=6-1=5.
∴ B(5,0).
把P(2,3)和B(5,0)分别代入直线l2:y=mx+n中,得
2m+n =3,
5m+n=0 .
解得
∴ l2对应的解析式为y=-x+5.
课时小结
1. 通过本节课,你收获了什么?学到了哪些方法, 体会到哪些思想,积累了哪些经验等等.
2. 你还有问题或者困惑吗?
这节课,从二元一次方程与一次函数的形式彼此互相转化,到二元一次方程的解与一次函数图象上的点彼此对应,最后将“枯燥” 的二元一次方程与“直观”的直线紧紧相连,打通“从数到形、从形到数”的畅通之路,正是本节课的主题.
教师寄语
自然界中“枝生连理,
花开并蒂”.而二元一次方
程与一次函数就是数学世界
的一株“并蒂花”.最终希
望在你们的心中开出一束永
不凋零的“数形”并蒂花.
19.2 一次函数
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第2课时
一次函数与二元一次方程(组)
导入新课
观察与思考
今天数学王国建了两个健身团,各个成员要按照
自己所在的集合加入对应粉丝团,这时来了“x+y=5”.
到我这里来
欢迎
加入
这是怎么回事?到底应该加到哪呢?
欢迎
加入
二元一
次方程
一次函数
二元一次方程与一次函数解析式的关系
数学活动一、
探究新知
1. 你能把二元一次方程x+y=5 改写成y= 的形式吗?
问题
5-x
2. 一次函数y=-x+5也可以通过变形得到相应的二元一次
方程ax+by=c的形式吗?
3. 任意的二元一次方程与对应的一次函数解析式都可以进行这样的转化吗?
总结:
每个二元一次方程都对应一个一次函数解析式,
每个一次函数解析式也对应着一个二元一次方程.
即二元一次方程与对应的一次函数解析式可以互相
转化.
一次函数图象上的点与二元一次方程的解的关系
数学活动二、
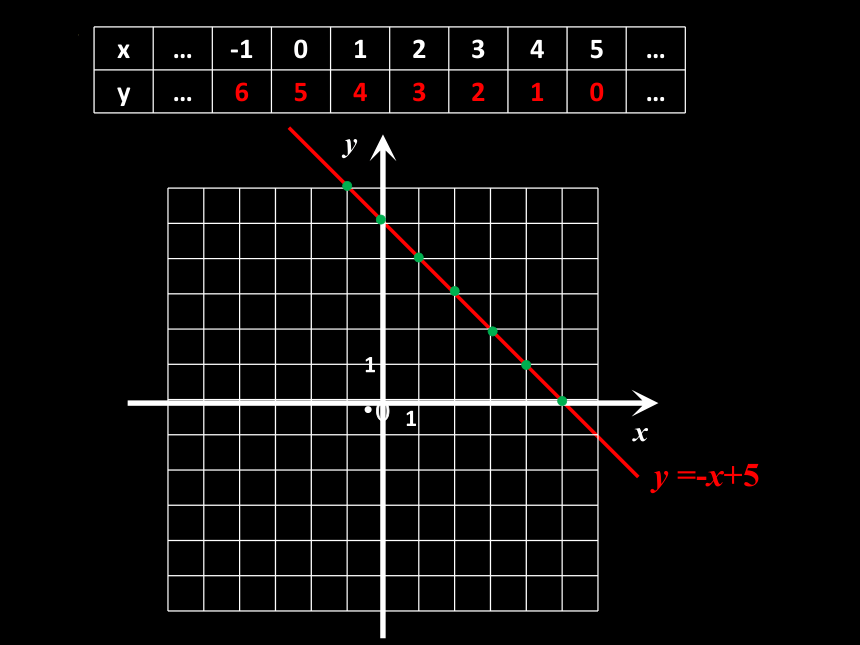
1. 二元一次方程x+y=5 的解有多少个?请你写出方程的
几个解,把以这几个解为坐标的点在坐标系中描出来.
问题
无数个解
…
O
x
y
1
1
y =-x+5
x … -1 0 1 2 3 4 5 …
y … 6 5 4 3 2 1 0 …
2. 如果再给出一些以方程的解为坐标的点,你能发现什么规律吗?
3. 这些点是否在某个一次函数图象上?为什么?
4. 反之,在一次函数y = -x + 5图象上任取一点,它的坐标适合方程x + y =5吗?
这些点在一条直线上.
在一次函数y=-x+5的图象上.
总结:
以二元一次方程的解为坐标的点都在相应的一次
函数图象上;一次函数图象上的点的坐标都适合相应
的二元一次方程.
二元一次方程组(的解)与一次函数(图象的交点)的关系
数学活动三、
1. 在同一坐标系中分别画出一次函数y=2x-1与y=5-x的图象,这两个图象有交点吗?
问题
x 5 0
y=5-x 0 5
x 1 0
y=2x -1 1 -1
(1)列表:
(2)描点;
O
x
y
1
1
y =-x+5
(2,3)
(3)连线;
y=2x-1
由方程组
y =-x+5,
y =2x-1,
解得
x =2,
y =3.
2. 交点坐标与二元一次方程组 的解有什么
关系?
y =-x+5,
y =2x-1,
方程组的解就是使方程组中两个方程同时成立的解,而这一对未知数也同时满足两个相应的一次函数解析式,因此方程组的解就是两个相应的一次函数图象的交点坐标.
3. 求二元一次方程组 的解,你有哪些方法?
x - y =-4,
2x+y =1,
加减消元法,
代入消元法,
图象法.
下面我们用图象法求解.
O
x
y
y =-2x+1
1
1
解:
由题可得:y =-2x+1和y =x+4.
在同一坐标系中画出两个一次函数图象如下:
y =x+4
两个一次函数图象
的交点为(-1,3).
(-1,3)
所以原二元一次方程组的解为
x =-1,
y =3.
但是由于画图的不准确性,
所求的解往往是近似解,
导致图象解法有一定的局限性.
用图象法求二元一次方程组的解的一般步骤:
(1)变函数:把方程组化为一次函数;
(2)画图象:
建立平面直角坐标系,画出两个一次函数的图象;
(3)找交点:由图象确定两条直线交点的坐标;
(4)写结论:依据交点的坐标写出方程组的解.
4.一次函数图象是直线,那么直线一定是一次函数吗?
不一定是一次函数.
如,直线x=2,直线y=-1等.
5.什么是二元一次方程组?
x =-1,
y =3,
是二元一次方程组吗?
x =-1,
y =3,
6. 二元一次方程组 的解是什么?
还能用图象法求该方程组的解吗?
O
x
y
1
1
x =-1
y =3
(-1,3)
1.一次函数图象是直线,但直线不一定是一次函数;
总结:
2.二元一次方程组对应两条直线,但不一定对应两个
一次函数.
4.一般地,从图形角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定两条直线交点的坐标.
3.由于图象解法的局限性.因此为了准确地解决有关图象
问题常常把它转化为代数问题来处理.
应用二元一次方程与一次函数的关系解决问题
数学活动四、
如图,直线y=k x + b与y=m x + n交于点(1,3),则
方程组 的解为 .
问题
O
x
y
y =kx+b
y =mx+n
1
1
y=k x + b
y=m x + n
x =1
y =3
(1,3)
如图,直线y=k x + b与y=m x + n交于点(1,3),则
方程组 的解为 .
变式:
O
x
y
y =kx+b
y =mx+n
1
1
y=-k x + b
y=-m x + n
x =-1
y =3
y=-k x + b
y=-m x + n
y=k(- x )+ b
y=m(- x )+ n
(1,3)
(-1,3)
二元一次方程组的解的三种情况
数学活动五、
问题
1. 二元一次方程组的解有哪些情况?
通过求下列二元一次方程组的解回忆一下.
无解
x =-1,
y =3;
x-y =-4;
2x+y =1,
①
x + y =2;
x + y =1,
②
2x +2y =2.
x + y =1,
③
无数个解
唯一解
2. 你能用画图象的方法求出以上二元一次方程组的解吗?
y =x+4
y =-2x+1
O
x
y
1
1
① y =-2x+1和y =x+4;
(-1,3)
k值不相等,两条直线不平行(相交),
有一个交点,对应方程组有唯一解.
y =-x+2
y =-x+1
O
x
y
1
1
② y =-x+1和y =-x+2;
k值相等,且b值不相等,两条直线平行,
无公共点,对应方程组无解.
y =-x+1
O
x
y
1
1
③ y =-x+1和y =-x+1.
k、b值均相等,两直线重合,
有无数个公共点,对应方程组无数个解.
由此,你发现了什么?
二元一次方程组
的解的个数
总结:
一次函数图象
的交点个数
唯一解
图象相交(有一个交点)
无解
图象平行(无交点)
无数个解
图象重合(有无数个交点)
检测反馈
B
2x +2y =3,
x + y =2,
1.若方程组 没有解,则一次函数
y=2-x和y= - x的图象必定( )
A.重合 B.平行 C.相交 D.无法确定
B
a2x -y =-b2,
a1x + y =b1,
2.直线y=-a1x+b1与直线y=a2x+b2若有唯一交点,则
二元一次方程组 的解的情况是( )
A.无解 B.有唯一解
C.有两组解 D.有无数组解
1号探测气球从海拔5 m 处出发,以1 m/min 的速度
上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
1号探测气球海拔高度:y =x+5( 0≤ x≤60 );
(1)用式子分别表示两个气球所在位置的海拔 y
(单位:m)关于上升时间 x(单位:min)
的函数关系.
2号探测气球海拔高度:y =0.5x+15 ( 0≤ x≤60 ) .
学以致用
(1)解:
答:当上升20min时,两个气球都位于海拔25m的高度 .
(2)由方程组
y =x+5,
(2)在某时刻,两个能否位于同一高度?这时的高度
是多少?如果能,这时气球上升了多长时间?位
于什么高度?
y =0.5x+15,
解得
x =20,
y =25.
两个图象的交点坐标为(20,25),这也说明当上升20min时,两个气球都位于海拔25m的高度 .
(20,25)
y =x+5 ( 0≤ x≤60 )
y =0.5x+15 ( 0≤ x≤60 )
10
40
O
x/min
y/m
10
30
20
20
30
40
我们也可以用一次函数的图象解释上述问题的解答.
50
60
50
60
两个图象
的交点坐
标为(20,25),
这也说明
当上20min
时,两个
气球都位
于海拔25
m的高度 .
素养提升
如图,直线l1:y=x+1与直线l2 :y=mx+n相交于点P(2,b).
(1)求b的值;
解:(1)把(2,b)代入y=x+1中,得b=2+1,
∴ b=3.
(2)直接写出方程组 的解;
mx-y +n=0
x-y+1 =0
(2)方程组的解为
x =2,
y =3.
l2
l1
O
x
y
b
2
A
B
P
(3)
m =-1,
n =5.
l2
l1
O
x
y
b
2
A
B
P
(3)若l1交x轴于点A, l2交x轴于点B,且
求l2对应的解析式.
∴ AB=6.
∵直线l1:y=x+1中,y=0时,x=-1.
∴ OA=1.
∴ OB=6-1=5.
∴ B(5,0).
把P(2,3)和B(5,0)分别代入直线l2:y=mx+n中,得
2m+n =3,
5m+n=0 .
解得
∴ l2对应的解析式为y=-x+5.
课时小结
1. 通过本节课,你收获了什么?学到了哪些方法, 体会到哪些思想,积累了哪些经验等等.
2. 你还有问题或者困惑吗?
这节课,从二元一次方程与一次函数的形式彼此互相转化,到二元一次方程的解与一次函数图象上的点彼此对应,最后将“枯燥” 的二元一次方程与“直观”的直线紧紧相连,打通“从数到形、从形到数”的畅通之路,正是本节课的主题.
教师寄语
自然界中“枝生连理,
花开并蒂”.而二元一次方
程与一次函数就是数学世界
的一株“并蒂花”.最终希
望在你们的心中开出一束永
不凋零的“数形”并蒂花.
