人教版数学七年级下册数学活动——不等式的应用课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级下册数学活动——不等式的应用课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
数学活动
——不等式的应用
R·七年级下册
情景导入
绿地率和我们息息相关,你知道绿地率是怎么求的吗?
我还经常遇到猜数游戏,要怎么猜的又快又好呢?
这节课我们通过两个活动,进一步了解和体验不等式的应用.
学习目标:
学会应用不等式解决实际生活中的一些问题.
学习重、难点:
把实际问题抽象为数学问题,并建立相应的模型予以解决.
探究新知
活动1
一元一次不等式组
统计资料表明,A省2005年城市建成区面积(简称建成区面积)为1316.4km2,城市建成区园林绿地面积(简称绿地面积)为373.48 km2,城市建成区园林绿地率(简称绿地率)为28.37%.该省2010年建成区面积增加了300 km2左右,绿地率超过了35%.
你能获得哪些信息?
1.2005年城市建成区面积为1316.4km2;
2.2005年绿地面积为373.48 km2;
3.城市建成区园林绿地率为28.37%;
4.2010年建成区面积增加了300km2左右,绿地率超过了35%.
问题
这五年(2005~2010年),A省增加的绿地面积超过了多少平方千米?
我们要怎么解这个问题呢?
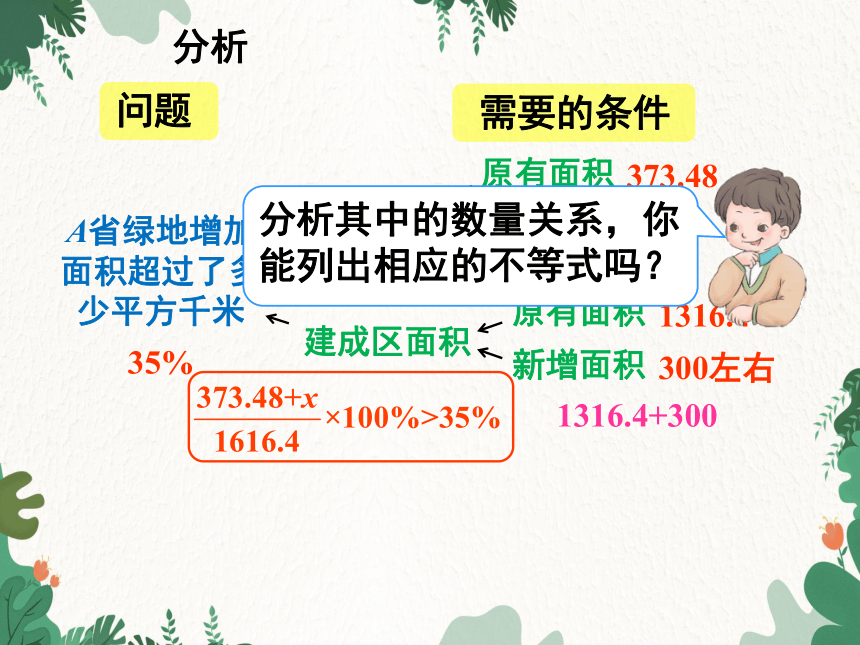
分析
A省绿地增加面积超过了多少平方千米
问题
需要的条件
35%
绿地面积
建成区面积
原有面积
新增面积
原有面积
新增面积
373.48
x
1316.4
300左右
373.48+x
1316.4+300
分析其中的数量关系,你能列出相应的不等式吗?
解上面的不等式,得x>192.26.
答:这五年(2005~2010年),A省绿地增加面积超过了192.26km2.
探究新知
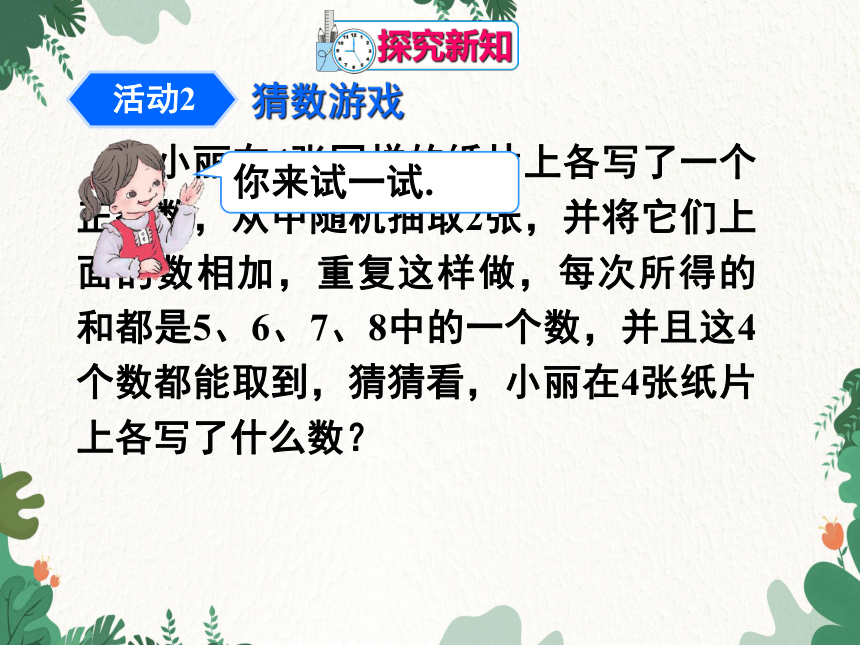
活动2
猜数游戏
小丽在4张同样的纸片上各写了一个正整数,从中随机抽取2张,并将它们上面的数相加,重复这样做,每次所得的和都是5、6、7、8中的一个数,并且这4个数都能取到,猜猜看,小丽在4张纸片上各写了什么数?
你来试一试.
设四个数分别为x,y,z,w,并且x≤y≤z≤w.
(1)若四个数互不相等,则所得的和至少有5种;
分析
通过以上分析,说明这四个数中有2个数相等.
(2)若四个数有两个数相等,则所得的和有4种;
(3)若四个数有三个数相等,则所得的和有2种;
(4)若四个数都相等,则所得的和有1种.
设四个数分别为x,y,z,w,并且x≤y≤z≤w.
结合前面的结论,有x+y≤x+z≤x+w(或y+z)≤y+w≤z+w,所以必有x+y≥5,z+w≤8.因为四个数都为整数,且只能是相邻两个数相等,所以x不可能等于y,且只有以下两种可能:
(1)若z=w,则z=w=4,于是
x+y=5
x+w=6
y+w=7
∴
x=2
y=3
w=4
z=4
(2)若y=z,则y=z=3,于是
x+y=5
x+w=7
z+w=8
∴
x=2
y=3
w=4
z=3
综上所述,这四个数是2,3,4,4或2,3,3,5.
基础巩固
随堂演练
1. 去年某市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少天?
解:设明年空气质量良好的天数比去年增加x天.
解不等式得:x>36.5,
答:明年空气质量良好的天数要比去年至少增加37天.
又∵x为整数.∴x≥37,
由题意得: .
综合运用
2. 小丽在4张同样的纸片上各写了一个正整数,从中随机抽取2张,并将它们上面的数相加,重复这样做,每次所得的和都是11,12,13,14,15中的一个数,并且这5个数都能取到,猜猜看,小丽在4张纸片上各写了什么数?若每次所得的和是11,12,13,14,15,16中的一个数,且这6个数都能取到呢?
解:设四个数为x,y,z,w,且x≤y≤z≤w,经分析得:x,y,z,w互不相等.
∴x+w=y+z,
∴x+y≤x+z≤x+w(或y+z)≤y+w≤z+w,
又∵每次所得的和都是11,12,13,14,15中的一个数,
∴
x+y=11
x+w=y+z=13
z+w=15
x+z=12
y+w=14
∴
x=5
y=6
w=8
z=7
∴4张纸片上分别写了5,6,7,8.
同理:当每次所得的和是11,12,13,14,15,16中的一个数时,这4张卡片上分别写了5,6,7,9.
课堂小结
通过这节课的学习活动,你有什么收获?
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费的增长点.据某市交通部门统计,截止到2016年底,全市的汽车拥有量已达216万辆,为了保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2018年底全市汽车拥有量不超过231.96万辆.
另据估计,从2017年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%,假定每年新增汽车数量相同,请你计算出该市从2017年初起每年新增汽车数量最多不能超过多少万辆.
解:设该市从2017年初起每年新增汽车数量为x万辆.
则到2017年底全市汽车拥有量为:
216-216×10%+x.
2018年底全市汽车拥有量为:
(216-216×10%+x)×(1-10%)+x.
根据题意,得:
(216-216×10%+x)×(1-10%)+x≤231.96
解得x≤30.
答:该市从2017年初起每年新增汽车数量最多不能超过30万辆.
1. 从课后习题中选取;
2. 完成练习册本课时的习题.
课后作业
本节课通过实践不等式的应用活动,让学生对不等式的解法,不等式解决实际生活中的问题有了更深的理解,在教学过程中,教师引导学生对不等式问题进行探索、研究,提高了学生的思维能力和解决实际问题的能力.
教学反思
数学活动
——不等式的应用
R·七年级下册
情景导入
绿地率和我们息息相关,你知道绿地率是怎么求的吗?
我还经常遇到猜数游戏,要怎么猜的又快又好呢?
这节课我们通过两个活动,进一步了解和体验不等式的应用.
学习目标:
学会应用不等式解决实际生活中的一些问题.
学习重、难点:
把实际问题抽象为数学问题,并建立相应的模型予以解决.
探究新知
活动1
一元一次不等式组
统计资料表明,A省2005年城市建成区面积(简称建成区面积)为1316.4km2,城市建成区园林绿地面积(简称绿地面积)为373.48 km2,城市建成区园林绿地率(简称绿地率)为28.37%.该省2010年建成区面积增加了300 km2左右,绿地率超过了35%.
你能获得哪些信息?
1.2005年城市建成区面积为1316.4km2;
2.2005年绿地面积为373.48 km2;
3.城市建成区园林绿地率为28.37%;
4.2010年建成区面积增加了300km2左右,绿地率超过了35%.
问题
这五年(2005~2010年),A省增加的绿地面积超过了多少平方千米?
我们要怎么解这个问题呢?
分析
A省绿地增加面积超过了多少平方千米
问题
需要的条件
35%
绿地面积
建成区面积
原有面积
新增面积
原有面积
新增面积
373.48
x
1316.4
300左右
373.48+x
1316.4+300
分析其中的数量关系,你能列出相应的不等式吗?
解上面的不等式,得x>192.26.
答:这五年(2005~2010年),A省绿地增加面积超过了192.26km2.
探究新知
活动2
猜数游戏
小丽在4张同样的纸片上各写了一个正整数,从中随机抽取2张,并将它们上面的数相加,重复这样做,每次所得的和都是5、6、7、8中的一个数,并且这4个数都能取到,猜猜看,小丽在4张纸片上各写了什么数?
你来试一试.
设四个数分别为x,y,z,w,并且x≤y≤z≤w.
(1)若四个数互不相等,则所得的和至少有5种;
分析
通过以上分析,说明这四个数中有2个数相等.
(2)若四个数有两个数相等,则所得的和有4种;
(3)若四个数有三个数相等,则所得的和有2种;
(4)若四个数都相等,则所得的和有1种.
设四个数分别为x,y,z,w,并且x≤y≤z≤w.
结合前面的结论,有x+y≤x+z≤x+w(或y+z)≤y+w≤z+w,所以必有x+y≥5,z+w≤8.因为四个数都为整数,且只能是相邻两个数相等,所以x不可能等于y,且只有以下两种可能:
(1)若z=w,则z=w=4,于是
x+y=5
x+w=6
y+w=7
∴
x=2
y=3
w=4
z=4
(2)若y=z,则y=z=3,于是
x+y=5
x+w=7
z+w=8
∴
x=2
y=3
w=4
z=3
综上所述,这四个数是2,3,4,4或2,3,3,5.
基础巩固
随堂演练
1. 去年某市空气质量良好(二级以上)的天数与全年天数(365天)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少天?
解:设明年空气质量良好的天数比去年增加x天.
解不等式得:x>36.5,
答:明年空气质量良好的天数要比去年至少增加37天.
又∵x为整数.∴x≥37,
由题意得: .
综合运用
2. 小丽在4张同样的纸片上各写了一个正整数,从中随机抽取2张,并将它们上面的数相加,重复这样做,每次所得的和都是11,12,13,14,15中的一个数,并且这5个数都能取到,猜猜看,小丽在4张纸片上各写了什么数?若每次所得的和是11,12,13,14,15,16中的一个数,且这6个数都能取到呢?
解:设四个数为x,y,z,w,且x≤y≤z≤w,经分析得:x,y,z,w互不相等.
∴x+w=y+z,
∴x+y≤x+z≤x+w(或y+z)≤y+w≤z+w,
又∵每次所得的和都是11,12,13,14,15中的一个数,
∴
x+y=11
x+w=y+z=13
z+w=15
x+z=12
y+w=14
∴
x=5
y=6
w=8
z=7
∴4张纸片上分别写了5,6,7,8.
同理:当每次所得的和是11,12,13,14,15,16中的一个数时,这4张卡片上分别写了5,6,7,9.
课堂小结
通过这节课的学习活动,你有什么收获?
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费的增长点.据某市交通部门统计,截止到2016年底,全市的汽车拥有量已达216万辆,为了保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2018年底全市汽车拥有量不超过231.96万辆.
另据估计,从2017年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%,假定每年新增汽车数量相同,请你计算出该市从2017年初起每年新增汽车数量最多不能超过多少万辆.
解:设该市从2017年初起每年新增汽车数量为x万辆.
则到2017年底全市汽车拥有量为:
216-216×10%+x.
2018年底全市汽车拥有量为:
(216-216×10%+x)×(1-10%)+x.
根据题意,得:
(216-216×10%+x)×(1-10%)+x≤231.96
解得x≤30.
答:该市从2017年初起每年新增汽车数量最多不能超过30万辆.
1. 从课后习题中选取;
2. 完成练习册本课时的习题.
课后作业
本节课通过实践不等式的应用活动,让学生对不等式的解法,不等式解决实际生活中的问题有了更深的理解,在教学过程中,教师引导学生对不等式问题进行探索、研究,提高了学生的思维能力和解决实际问题的能力.
教学反思
