5.3.3古典概型 课件(共18张PPT)
文档属性
| 名称 | 5.3.3古典概型 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 10:48:45 | ||
图片预览





文档简介
(共18张PPT)
古典概型
一、问题驱动 引入模型
规则1:
掷一枚质地均匀的硬币,正面朝上就给甲,反面朝上就给乙.
规则2:
两个人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙.
请你利用本节课的内容判断哪个规则公平与合理?
问题情境
一张电影票,甲乙同学都想得到它,为了公平,他们提出了两个规则。
任务1:归纳古典概型的特征
二、比较分析 初识模型
问题1:抛掷一枚质地均匀的硬币,有多少个基本事件?哪一个基本事件出现的可能性大些?
正面朝上
反面朝上
问题2:抛掷一枚质地均匀的骰子,有多少个基本事件?哪一个基本事件出现的可能性大些?
4点
1点
2点
3点
5点
6点
问题3:比较与分析前面两个试验,从基本事件的角度,归纳与概括共同特点
2个基本事件
可能性相等
6个基本事件
可能性相等
任务1:归纳古典概型的特征
问题3:比较与分析前面两个试验,从基本事件的角度,归纳与概括共同特点
(1)试验中所有可能出现的基本事件只有有限个.
(2)每个基本事件出现的可能性相等.
具有这两个特点的概率模型称为古典概率模型(classical models of probability),
简称古典概型.
三、归纳概括 构建模型
有限性
等可能性
任务2:深刻理解古典概型的特征
四、正反举例 辨析模型
问题4:请列举一个你身边的古典概型的例子?
问题5:辨析模型是否是古典概型?
(1)如图,向一个圆面内随机地投射一个飞镖,如果该飞镖落在圆内任意一点都是等可能的,你认为这是古典概型吗 为什么?
有限性
等可能性
四、正反举例 辨析模型
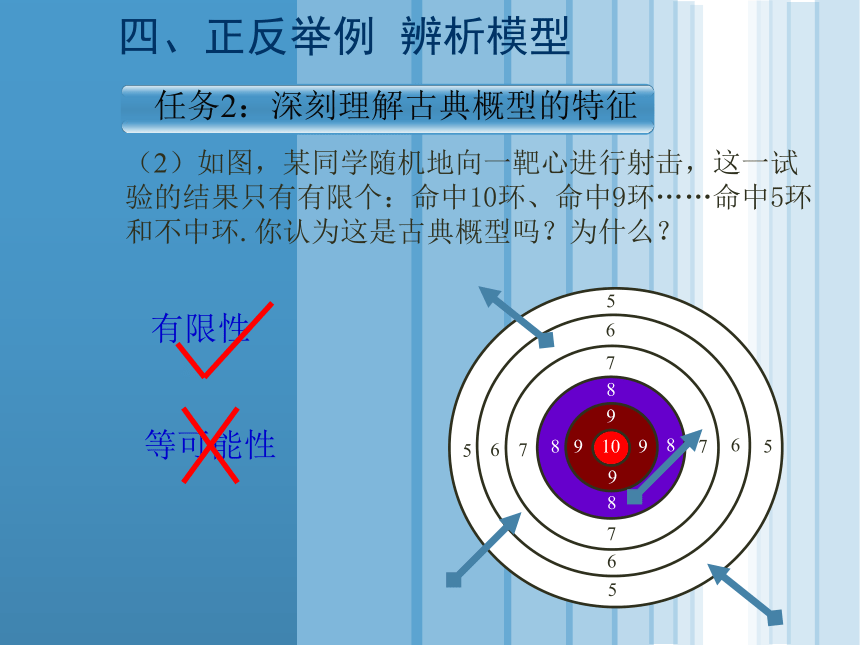
(2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么?
10
9
9
9
9
8
8
8
8
7
7
7
7
6
6
6
6
5
5
5
5
有限性
等可能性
任务2:深刻理解古典概型的特征
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
问题6:在掷硬币试验中,出现正面朝上的概率与反面朝上的概率是多少?在掷骰子试验中,出现各个点的概率是多少?
分析:
在掷硬币试验中,根据古典概型的特征,
P(“正面朝上”)= P(“ 反面朝上”)
根据概率的加法公式,
P(“正面朝上”)+P(“反面朝上” )= P(“必然事件”)=1
所以P(“正面朝上”)= P(“ 反面朝上”)=
1
2
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
同理,在掷骰子试验中,
P(“1点”) =P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)=
1
6
问题6:在掷硬币试验中,出现正面朝上的概率与反面朝上的概率是多少?在掷骰子试验中,出现各个点的概率是多少?
在掷硬币试验中,
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
在掷骰子试验中,
P(“1点”)=
“向上点数为1”所包含的基本事件的个数
基本事件的总数
1
6
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
P(“向上点数为偶数点”)
=
P(“2点”)+
P(“4点”)+
P(“6点”)
“向上点数为偶数点”所包含的基本事件的个数
基本事件的总数
=
在掷硬币试验中,
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
在掷骰子试验中,
P(“1点”)=
“向上点数为1”所包含的基本事件的个数
基本事件的总数
1
6
=
+
+
1
6
1
6
=
1
6
3
6
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
问题7:根据上述古典概型事件的概率计算过程,能否归纳和概括出计算古典概型事件的概率计算公式?
P(A)=
A所包含的基本事件个数
基本事件的总数
一、问题驱动 引入模型
规则1:
掷一枚质地均匀的硬币,正面朝上就给甲,反面朝上就给乙.
规则2:
两个人同时掷两个质地均匀的骰子,点数之和为6点就给甲,点数之和为7点就给乙.
请利用本节课知识判断哪个规则公平?
问题情境
一张电影票,甲乙同学都想得到它,为了公平,他们提出了两个规则。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法1:列表枚举
P(“点数之和为7点”)=
“点数之和为7点”所包含的基本事件的个数
基本事件的总数
6
36
=
“点数之和为6点”所包含的基本事件的个数
基本事件的总数
5
36
=
P(“点数之和为6点”)=
红色 骰子 蓝色骰子
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法2:树状图
P(“点数之和为7点”)=
“点数之和为7点”所包含的基本事件的个数
基本事件的总数
6
36
=
“点数之和为6点”所包含的基本事件的个数
基本事件的总数
5
36
=
P(“点数之和为6点”)=
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
开始
1
2
3
4
5
6
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法3:对称法
1
3
2
4
5
6
1
2
3
4
5
6
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
9
5
6
7
8
9
10
6
7
8
9
10
11
7
8
9
10
11
12
第 一 次 抛 掷 后 向 上 的 数
第 二 次 抛 掷 后 向 上 的 数
P(“点数之和为6点”)=
5
36
P(“点数之和为7点”)=
36
6
规则2不公平!
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
【小结】在使用古典概型的概率公式时,一般过程是怎样的?
(1)审清题意,判断是否为古典概型(判)
(2)计算试验所有基本事件的总数n(总)
(5)小结作答(答)
(3)计算事件 所包含的基本事件个数m(分)
(4)应用公式 计算(用)
P(A)=
m
n
任务5:画出本节知识框图。
七、回顾反思 小结模型
古典概型
自然语言
基本事件
有限性、等可能性
A的基本事件个数
基本事件的总数
集合语言
集合A中的元素个数
集合I中的元素个数
I
A
数学图形
频率与概率
生活体验
实物情境
五部曲求概率
归纳思想、枚举法
八、分层作业 小结模型
A.必做题:完成课本130页练习1、2、3;
B.选做题(问题10):考虑三个人,每人掷一次骰子,猜点数和.请问出现点数之和是几的概率最大,为什么?
C.挑战题:以小组为单位为某大型儿童商场设计一个“六一”商场促销的抽奖活动计划,并计算相应的获奖概率。
祝同学们学习进步!
古典概型
一、问题驱动 引入模型
规则1:
掷一枚质地均匀的硬币,正面朝上就给甲,反面朝上就给乙.
规则2:
两个人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙.
请你利用本节课的内容判断哪个规则公平与合理?
问题情境
一张电影票,甲乙同学都想得到它,为了公平,他们提出了两个规则。
任务1:归纳古典概型的特征
二、比较分析 初识模型
问题1:抛掷一枚质地均匀的硬币,有多少个基本事件?哪一个基本事件出现的可能性大些?
正面朝上
反面朝上
问题2:抛掷一枚质地均匀的骰子,有多少个基本事件?哪一个基本事件出现的可能性大些?
4点
1点
2点
3点
5点
6点
问题3:比较与分析前面两个试验,从基本事件的角度,归纳与概括共同特点
2个基本事件
可能性相等
6个基本事件
可能性相等
任务1:归纳古典概型的特征
问题3:比较与分析前面两个试验,从基本事件的角度,归纳与概括共同特点
(1)试验中所有可能出现的基本事件只有有限个.
(2)每个基本事件出现的可能性相等.
具有这两个特点的概率模型称为古典概率模型(classical models of probability),
简称古典概型.
三、归纳概括 构建模型
有限性
等可能性
任务2:深刻理解古典概型的特征
四、正反举例 辨析模型
问题4:请列举一个你身边的古典概型的例子?
问题5:辨析模型是否是古典概型?
(1)如图,向一个圆面内随机地投射一个飞镖,如果该飞镖落在圆内任意一点都是等可能的,你认为这是古典概型吗 为什么?
有限性
等可能性
四、正反举例 辨析模型
(2)如图,某同学随机地向一靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环.你认为这是古典概型吗?为什么?
10
9
9
9
9
8
8
8
8
7
7
7
7
6
6
6
6
5
5
5
5
有限性
等可能性
任务2:深刻理解古典概型的特征
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
问题6:在掷硬币试验中,出现正面朝上的概率与反面朝上的概率是多少?在掷骰子试验中,出现各个点的概率是多少?
分析:
在掷硬币试验中,根据古典概型的特征,
P(“正面朝上”)= P(“ 反面朝上”)
根据概率的加法公式,
P(“正面朝上”)+P(“反面朝上” )= P(“必然事件”)=1
所以P(“正面朝上”)= P(“ 反面朝上”)=
1
2
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
同理,在掷骰子试验中,
P(“1点”) =P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)=
1
6
问题6:在掷硬币试验中,出现正面朝上的概率与反面朝上的概率是多少?在掷骰子试验中,出现各个点的概率是多少?
在掷硬币试验中,
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
在掷骰子试验中,
P(“1点”)=
“向上点数为1”所包含的基本事件的个数
基本事件的总数
1
6
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
P(“向上点数为偶数点”)
=
P(“2点”)+
P(“4点”)+
P(“6点”)
“向上点数为偶数点”所包含的基本事件的个数
基本事件的总数
=
在掷硬币试验中,
P(“正面朝上”)=
“出现正面朝上”所包含的基本事件的个数
基本事件的总数
1
2
=
在掷骰子试验中,
P(“1点”)=
“向上点数为1”所包含的基本事件的个数
基本事件的总数
1
6
=
+
+
1
6
1
6
=
1
6
3
6
=
任务3:尝试推理古典概型概率的计算公式
五、归纳类比 推理模型
问题7:根据上述古典概型事件的概率计算过程,能否归纳和概括出计算古典概型事件的概率计算公式?
P(A)=
A所包含的基本事件个数
基本事件的总数
一、问题驱动 引入模型
规则1:
掷一枚质地均匀的硬币,正面朝上就给甲,反面朝上就给乙.
规则2:
两个人同时掷两个质地均匀的骰子,点数之和为6点就给甲,点数之和为7点就给乙.
请利用本节课知识判断哪个规则公平?
问题情境
一张电影票,甲乙同学都想得到它,为了公平,他们提出了两个规则。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法1:列表枚举
P(“点数之和为7点”)=
“点数之和为7点”所包含的基本事件的个数
基本事件的总数
6
36
=
“点数之和为6点”所包含的基本事件的个数
基本事件的总数
5
36
=
P(“点数之和为6点”)=
红色 骰子 蓝色骰子
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法2:树状图
P(“点数之和为7点”)=
“点数之和为7点”所包含的基本事件的个数
基本事件的总数
6
36
=
“点数之和为6点”所包含的基本事件的个数
基本事件的总数
5
36
=
P(“点数之和为6点”)=
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
开始
1
2
3
4
5
6
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
任务4:用所学知识解决课前问题
六、变式训练 学用模型
方法3:对称法
1
3
2
4
5
6
1
2
3
4
5
6
2
3
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
9
5
6
7
8
9
10
6
7
8
9
10
11
7
8
9
10
11
12
第 一 次 抛 掷 后 向 上 的 数
第 二 次 抛 掷 后 向 上 的 数
P(“点数之和为6点”)=
5
36
P(“点数之和为7点”)=
36
6
规则2不公平!
规则2:两人同时掷两个质地均匀的骰子,点数之和为6就给甲,点数之和为7就给乙。
任务4:用所学知识解决课前问题
六、变式训练 学用模型
【小结】在使用古典概型的概率公式时,一般过程是怎样的?
(1)审清题意,判断是否为古典概型(判)
(2)计算试验所有基本事件的总数n(总)
(5)小结作答(答)
(3)计算事件 所包含的基本事件个数m(分)
(4)应用公式 计算(用)
P(A)=
m
n
任务5:画出本节知识框图。
七、回顾反思 小结模型
古典概型
自然语言
基本事件
有限性、等可能性
A的基本事件个数
基本事件的总数
集合语言
集合A中的元素个数
集合I中的元素个数
I
A
数学图形
频率与概率
生活体验
实物情境
五部曲求概率
归纳思想、枚举法
八、分层作业 小结模型
A.必做题:完成课本130页练习1、2、3;
B.选做题(问题10):考虑三个人,每人掷一次骰子,猜点数和.请问出现点数之和是几的概率最大,为什么?
C.挑战题:以小组为单位为某大型儿童商场设计一个“六一”商场促销的抽奖活动计划,并计算相应的获奖概率。
祝同学们学习进步!
