冀教版数学四年级下册 4.3三角形的内角和 课件(22张PPT)
文档属性
| 名称 | 冀教版数学四年级下册 4.3三角形的内角和 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 434.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
4 多边形
4.3 三角形的内角和
学习目标
1、通过操作活动探索发现和验证“三角形的内角和是180度”的规律。
2、在操作活动中,培养学生的合作能力、动手实践能力,发展学生的空间观念。并运用新知识解决问题。
3.使学生有科学实验态度,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
你用什么方法来验证这个猜想?
三角形的三个内角和是多少度?
猜一猜:
情景导入
1.画一个三角形。
2.用量角器测量出所画的三角形每个内角的度数。
一、量一量
三角形 ∠1 ∠2 ∠3 三角之和
探索新知
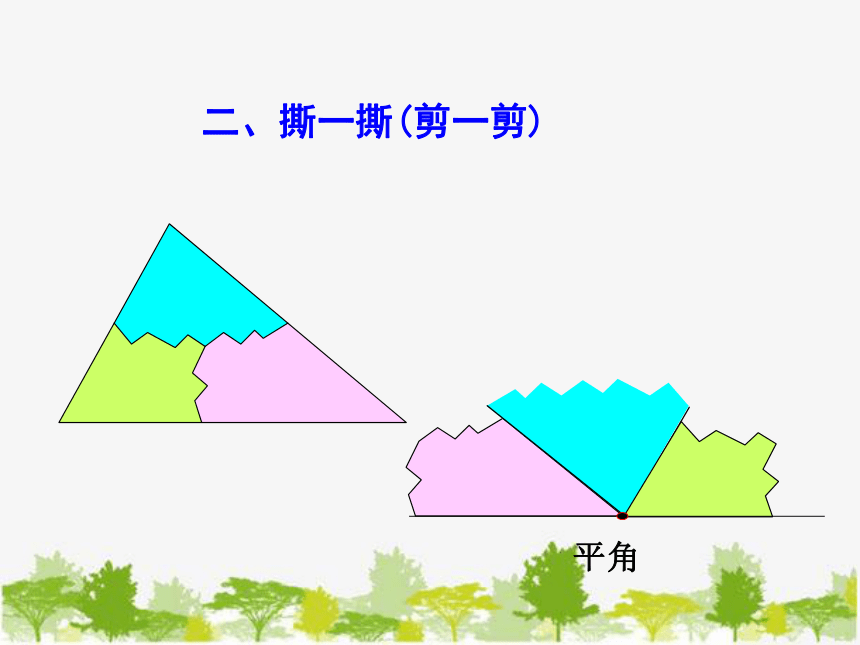
平角
二、撕一撕(剪一剪)
1
1
2
2
3
3
中点
中点
中点
中点
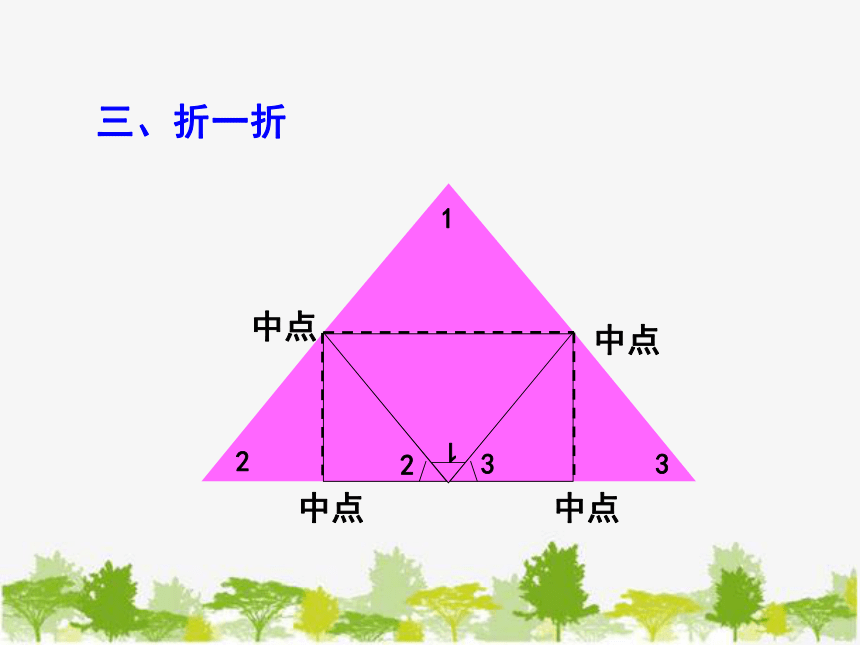
三、折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
(2) 60°,70°,90°
(3) 30°,40°,50°
(4) 50°,50°,80°
(5) 60°,60°,60°
(1) 80°,95°,5°
1.(口答)下列各组角能是同一个三角形的内角吗?为什么?
典题精讲
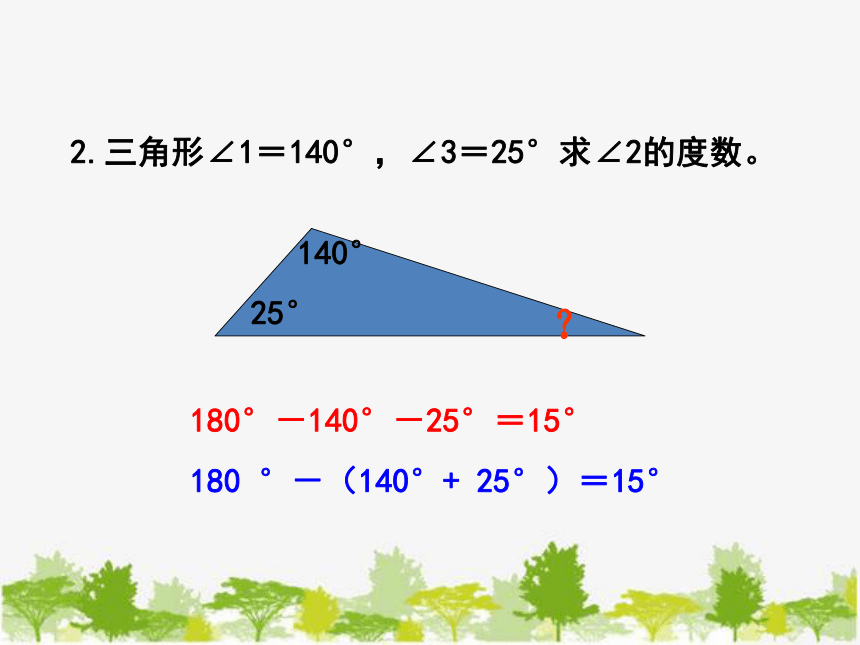
2.三角形∠1=140°,∠3=25°求∠2的度数。
140°
25°
?
180°-140°-25°=15°
180 °-(140°+ 25°)=15°
3 .爸爸给小红买了一个等腰三角形的风筝,它的一个底角是70°,顶角多少度?
180°- 70°- 70°= 40°
70°
70°
?
180°- 70°× 2 = 40°
4.某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去。为什么?
③
180°× 2 = 360°
两个三角形
根据三角形内角和是 180 °,你能求出下面四边形的内角和吗?
情景导入2
30°
60°
90°
45°
90°
45°
每个三角尺的内角度数之和都是180°。
你知道三角尺内角的度数分别是多少吗?
探索新知
30°
30°
60°
60°
拼成的大三角形内角和是多少?
内角和怎么还是180°?
(一)明确结论
1. 画几个不同类型的三角形。量一量,算一算,三角形3个内角和各是多少度。
三角形 ∠1 ∠2 ∠3 三角之和
(一)明确结论
2. 先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角。
1
3
2
拼成了一个平角。
三角形的内角和是180°。
任意直角三角形的内角和是180°。
长方形的四个角都是直角,所以长方形的内角和应为:90°×4=360°。将长方形沿对角线分割,可以分成两个完全相等的三角形,所以直角三角形内角和应为:360°÷2=180°。
(二)方法拓展
1
4
任意三角形的内角和是180 °。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
1
2
3
4
2
3
(二)方法拓展
1. 在下图中,其中∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
学以致用
2. 这有一条红领巾,它的形状是等腰三角形,其中∠1=110°,请计算出∠2=( )°,∠3=( )°。
2
3
1
(180°-110°)÷2=35°
35
35
3. 剪一剪。
把一个三角形纸板沿直线剪一刀,剩下的纸板的内角和是多少度
可能是三角形,内角和是180°,也可能是其他的情况。
课堂小结
今天你都收获了什么?
本节课学的内容,你理解了吗?同学之间互相讨论一下!
4 多边形
4.3 三角形的内角和
学习目标
1、通过操作活动探索发现和验证“三角形的内角和是180度”的规律。
2、在操作活动中,培养学生的合作能力、动手实践能力,发展学生的空间观念。并运用新知识解决问题。
3.使学生有科学实验态度,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
你用什么方法来验证这个猜想?
三角形的三个内角和是多少度?
猜一猜:
情景导入
1.画一个三角形。
2.用量角器测量出所画的三角形每个内角的度数。
一、量一量
三角形 ∠1 ∠2 ∠3 三角之和
探索新知
平角
二、撕一撕(剪一剪)
1
1
2
2
3
3
中点
中点
中点
中点
三、折一折
三角形的内角和是180°。
∠1+∠2+∠3=180°
(2) 60°,70°,90°
(3) 30°,40°,50°
(4) 50°,50°,80°
(5) 60°,60°,60°
(1) 80°,95°,5°
1.(口答)下列各组角能是同一个三角形的内角吗?为什么?
典题精讲
2.三角形∠1=140°,∠3=25°求∠2的度数。
140°
25°
?
180°-140°-25°=15°
180 °-(140°+ 25°)=15°
3 .爸爸给小红买了一个等腰三角形的风筝,它的一个底角是70°,顶角多少度?
180°- 70°- 70°= 40°
70°
70°
?
180°- 70°× 2 = 40°
4.某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去。为什么?
③
180°× 2 = 360°
两个三角形
根据三角形内角和是 180 °,你能求出下面四边形的内角和吗?
情景导入2
30°
60°
90°
45°
90°
45°
每个三角尺的内角度数之和都是180°。
你知道三角尺内角的度数分别是多少吗?
探索新知
30°
30°
60°
60°
拼成的大三角形内角和是多少?
内角和怎么还是180°?
(一)明确结论
1. 画几个不同类型的三角形。量一量,算一算,三角形3个内角和各是多少度。
三角形 ∠1 ∠2 ∠3 三角之和
(一)明确结论
2. 先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角。
1
3
2
拼成了一个平角。
三角形的内角和是180°。
任意直角三角形的内角和是180°。
长方形的四个角都是直角,所以长方形的内角和应为:90°×4=360°。将长方形沿对角线分割,可以分成两个完全相等的三角形,所以直角三角形内角和应为:360°÷2=180°。
(二)方法拓展
1
4
任意三角形的内角和是180 °。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
1
2
3
4
2
3
(二)方法拓展
1. 在下图中,其中∠1=140°,∠3=25°。求∠2的度数。
180°-140°-25°=15°
学以致用
2. 这有一条红领巾,它的形状是等腰三角形,其中∠1=110°,请计算出∠2=( )°,∠3=( )°。
2
3
1
(180°-110°)÷2=35°
35
35
3. 剪一剪。
把一个三角形纸板沿直线剪一刀,剩下的纸板的内角和是多少度
可能是三角形,内角和是180°,也可能是其他的情况。
课堂小结
今天你都收获了什么?
本节课学的内容,你理解了吗?同学之间互相讨论一下!
