4.3角同步训练(附答案)
文档属性
| 名称 | 4.3角同步训练(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-30 23:25:09 | ||
图片预览



文档简介
4.3角同步训练(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图一束光线射在平面镜上,这时光线的入射角(入射光线与法线ON的夹角)与光的反射角(反射光线与法线ON的夹角)是相同的,如果这束光线与镜面成30°角射到平面镜上,则入射角α与β的度数为( )
A.30° B.60°C.45° D.65°
2、如图,已知∠AOC=90°,∠BOC=a,OD平分∠AOB,则∠COD=( )
A. ?????????????? B. ????????? C. ???????? D.
3、已知与互余,=,则=??( )? 度;
4、若一个角的补角的余角是28o,则这个角的度数为????? (? )
A.62o???????????? B.72o??????????? C.118o????????????? D.128o
5、如图,下列说法中错误的是(??? )
A.OB方向是北偏西15o????????? B.OA方向是北偏东30o
C.OC方向是南偏西25o????????? D.OD方向是东南方向
6、如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是(? )
A.20°???? ??????? B.25°???????? C.30° ??????????? ??? D.70°
7、用A、B、C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25,小红家在小明家正东,小红家在学校北偏东35,则∠BAC=(???? )
A.35;????????? B.55;?????????? C.60;?????????? D.65.
8、?如果∠α和∠互补,且∠α>∠,则下列表示∠的余角的式子中:
①90°-∠;②∠α-90°;③180°-∠α;④(∠α-∠).正确的是:(???? )
A.①②③④ B. ①②④ C. .①②③?? D. ①②
9、?在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的(??? )
A. 南偏西50度方向???? ??? B. 南偏西40度方向
C. 北偏东50度方向?????? ?? D. 北偏东40度方向
10、如果一个角的余角是50°,那么这个补角的角是????? (?? ????)
A.160°??????????? B.150°??????????? C.140°???????? D.130°
二、填空题
11、2点20分,时针与分针所成的角为_________度.
12、小明今天早上七点二十出门上班,请问此时时针与分针的夹角为__________度。
13、一个角的补角比它的余角的3倍大10°,则这个角等于________.
14、如图,,是的平分线,则??????? 度。
15、如图,OA⊥OB,若射线OA的方向为北偏东65°,则射线OB的方向为????? ??.
16、如图,将一副三角板的直角顶点重合,摆放在桌面上。若∠AOD=140°,则∠BOC=?????
.
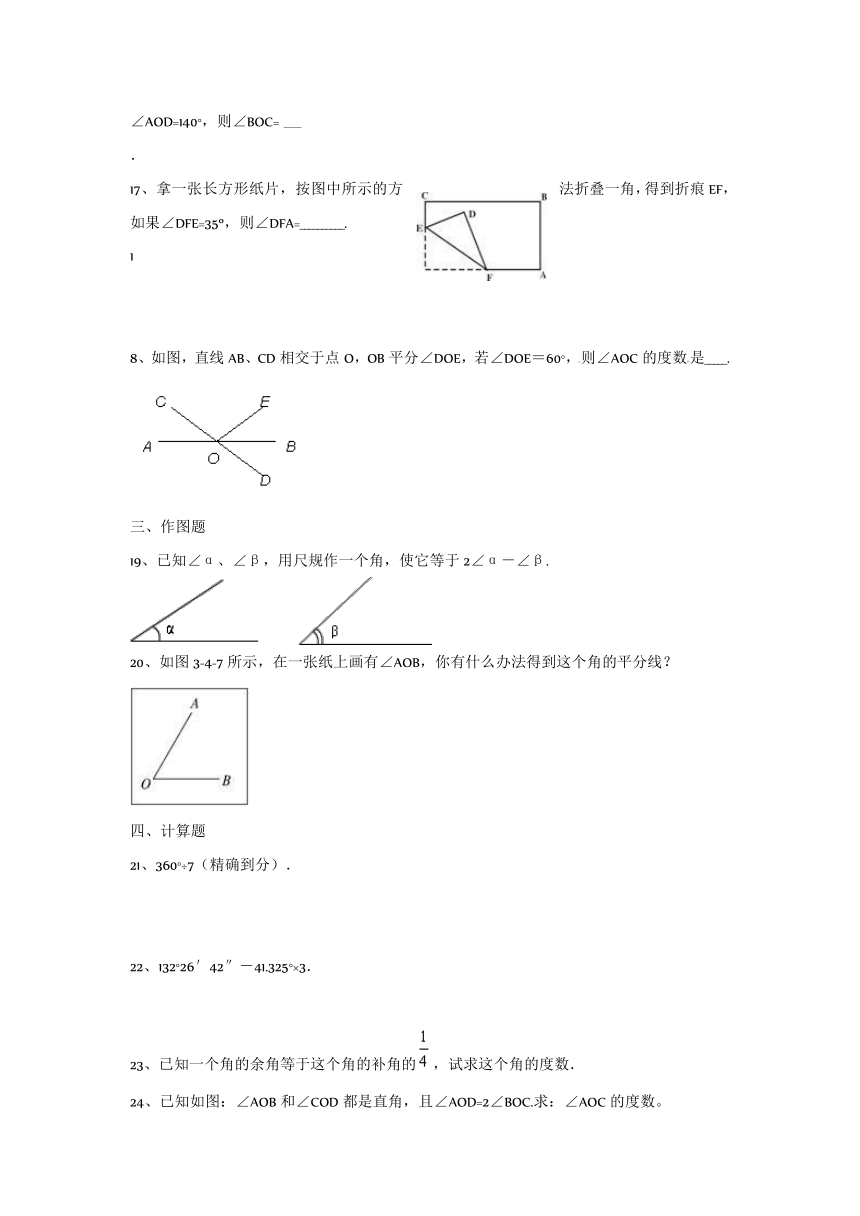
17、拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,如果∠DFE=35o,则∠DFA=__________.
1
8、如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是_____.
三、作图题
19、已知∠α、∠β,用尺规作一个角,使它等于2∠α-∠β.
20、如图3-4-7所示,在一张纸上画有∠AOB,你有什么办法得到这个角的平分线?
四、计算题
21、360°÷7(精确到分).
22、132°26′42″-41.325°×3.
23、已知一个角的余角等于这个角的补角的,试求这个角的度数.
24、已知如图:∠AOB和∠COD都是直角,且∠AOD=2∠BOC.求:∠AOC的度数。
五、简答题
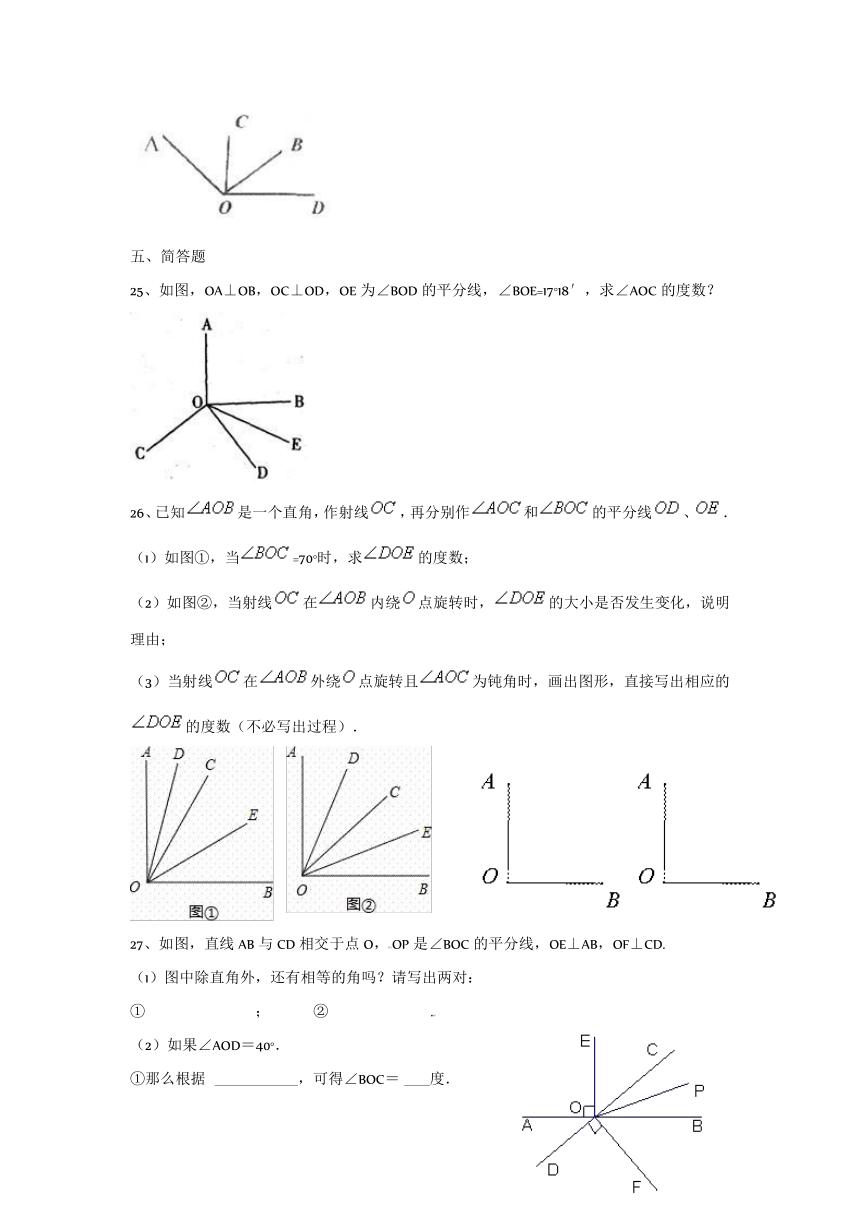
25、如图,OA⊥OB,OC⊥OD,OE为∠BOD的平分线,∠BOE=17°18′,求∠AOC的度数?
26、已知是一个直角,作射线,再分别作和的平分线、.
(1)如图①,当=70°时,求的度数;
(2)如图②,当射线在内绕点旋转时,的大小是否发生变化,说明理由;
(3)当射线在外绕点旋转且为钝角时,画出图形,直接写出相应的的度数(不必写出过程).
27、如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
①??????????????????????? ;???????? ②???????????????????????.
(2)如果∠AOD=40°.
①那么根据????????????????? ??,可得∠BOC=????? 度.
②因为OP是∠BOC的平分线,
所以∠COP=∠???????? =???????? 度.
③求∠BOF的度数.
28、如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有_________个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数=_________,∠BOE的度数=_________;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
29、如图,为直线上一点,平分,,,求的度数.
30、如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
31、已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C、E、F在直线AB的同侧(如图1所示)
①若∠COF=25°,求∠BOE的度数.
②若∠COF=α°,则∠BOE=????????? °.
(2)当点C与点E、F在直线AB的两旁(如图2所示)时,(1)中第②式的结论是否仍然成立?请给出你的结论并说明理由.
参考答案
一、选择题
1、B
2、B
3、60,
4、C
5、?B
6、D
7、C;
8、B
9、?B
10、C
二、填空题
11、
12、?100
13、50
14、30
15、南偏东25°
16、50°
17、110°
18、30°;
三、作图题
19、
20、思路解析:可利用本节所学知识,也可以利用其他方法.
答案:方法一:将∠AOB折叠,使射线OA、OB重合,再以O为端点,在∠AOB的内部沿折痕画一条射线,即为∠AOB的平分线;
方法二:用量角器先量出∠AOB的大小,再以OA或OB为一边作一个角等于∠AOB的一半,这个角的另一边即为∠AOB的平分线.
四、计算题
21、360°÷7
=51°+3°÷7
=51°+25′+5′÷7
=51°+25′+300″÷7
≈51°+25′+43″
≈51°26′.
22、解法一? 132°26′42″-41.325°×3
=132.445°-123.975°
=8.47°.
解法二? 132°26′42″-41.325°×3
=132°26′42″-123.975°
=132°26′42″-123°58′30″
=131°86′42″-123°58′30″
=8°28′12″.
23、
24、解:设∠AOC的度数为,根据题意得:
解之:=6?? 答:(略)
五、简答题
25、∵OE平分∠BOD,∴∠BOD=2∠BOE=217°18′=34°36′(2分)
又∵∠AOC+∠AOB+∠DOC+∠BOD=360°且OA⊥OB,OC⊥OD
即∠AOB=∠DOC=90°,∴∠AOC+∠BOD=180°(4分)
∠AOC=180°-34°36′=145°24′(6分)
26、解:(1)如图,
,
(2)的大小不变,理由是:
(3)的大小发生变化情况为, 如图3,则为45°;如图4,则为135度.
27、(1)①∠BOF=∠EOC;???????? ②∠BOP=∠COP.
(2) ①对顶角相等,? 40.???? ②∠BOC? 20???? ③500
28、(1)9;
(2)65°,65°;
(3)结论:OE平分∠BOC.
理由:设∠AOC=2α,
∵OD平分∠AOC,∠AOC =2α,
∴∠AOD=∠COD ==α,
又∵∠DOE=90°
∴∠COE =∠DOE-∠COD =90°-α.
又∵∠BOE =180°-∠DOE-∠AOD=180°-90°-α=90°-α,
∴∠COE=∠BOE,即OE平分∠BOC.
29、解:由题意可知,∠AOE=180°
又∵;∴∠BOD=90°
又∵平分
∴∠BOC=∠BOD=45°
又∵,∴∠1=46°
∴=∠AOB+∠BOC=46°+45°=91°
30、解:(1)9?
(2)155°
(3)平分
31、(1)①∠BOE=50°? ②∠BOE=2α°
(2)当点C与点E、F在直线AB的两旁时,第②式的结论仍然成立,
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图一束光线射在平面镜上,这时光线的入射角(入射光线与法线ON的夹角)与光的反射角(反射光线与法线ON的夹角)是相同的,如果这束光线与镜面成30°角射到平面镜上,则入射角α与β的度数为( )
A.30° B.60°C.45° D.65°
2、如图,已知∠AOC=90°,∠BOC=a,OD平分∠AOB,则∠COD=( )
A. ?????????????? B. ????????? C. ???????? D.
3、已知与互余,=,则=??( )? 度;
4、若一个角的补角的余角是28o,则这个角的度数为????? (? )
A.62o???????????? B.72o??????????? C.118o????????????? D.128o
5、如图,下列说法中错误的是(??? )
A.OB方向是北偏西15o????????? B.OA方向是北偏东30o
C.OC方向是南偏西25o????????? D.OD方向是东南方向
6、如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是(? )
A.20°???? ??????? B.25°???????? C.30° ??????????? ??? D.70°
7、用A、B、C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25,小红家在小明家正东,小红家在学校北偏东35,则∠BAC=(???? )
A.35;????????? B.55;?????????? C.60;?????????? D.65.
8、?如果∠α和∠互补,且∠α>∠,则下列表示∠的余角的式子中:
①90°-∠;②∠α-90°;③180°-∠α;④(∠α-∠).正确的是:(???? )
A.①②③④ B. ①②④ C. .①②③?? D. ①②
9、?在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的(??? )
A. 南偏西50度方向???? ??? B. 南偏西40度方向
C. 北偏东50度方向?????? ?? D. 北偏东40度方向
10、如果一个角的余角是50°,那么这个补角的角是????? (?? ????)
A.160°??????????? B.150°??????????? C.140°???????? D.130°
二、填空题
11、2点20分,时针与分针所成的角为_________度.
12、小明今天早上七点二十出门上班,请问此时时针与分针的夹角为__________度。
13、一个角的补角比它的余角的3倍大10°,则这个角等于________.
14、如图,,是的平分线,则??????? 度。
15、如图,OA⊥OB,若射线OA的方向为北偏东65°,则射线OB的方向为????? ??.
16、如图,将一副三角板的直角顶点重合,摆放在桌面上。若∠AOD=140°,则∠BOC=?????
.
17、拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,如果∠DFE=35o,则∠DFA=__________.
1
8、如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是_____.
三、作图题
19、已知∠α、∠β,用尺规作一个角,使它等于2∠α-∠β.
20、如图3-4-7所示,在一张纸上画有∠AOB,你有什么办法得到这个角的平分线?
四、计算题
21、360°÷7(精确到分).
22、132°26′42″-41.325°×3.
23、已知一个角的余角等于这个角的补角的,试求这个角的度数.
24、已知如图:∠AOB和∠COD都是直角,且∠AOD=2∠BOC.求:∠AOC的度数。
五、简答题
25、如图,OA⊥OB,OC⊥OD,OE为∠BOD的平分线,∠BOE=17°18′,求∠AOC的度数?
26、已知是一个直角,作射线,再分别作和的平分线、.
(1)如图①,当=70°时,求的度数;
(2)如图②,当射线在内绕点旋转时,的大小是否发生变化,说明理由;
(3)当射线在外绕点旋转且为钝角时,画出图形,直接写出相应的的度数(不必写出过程).
27、如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
①??????????????????????? ;???????? ②???????????????????????.
(2)如果∠AOD=40°.
①那么根据????????????????? ??,可得∠BOC=????? 度.
②因为OP是∠BOC的平分线,
所以∠COP=∠???????? =???????? 度.
③求∠BOF的度数.
28、如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有_________个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数=_________,∠BOE的度数=_________;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
29、如图,为直线上一点,平分,,,求的度数.
30、如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
31、已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C、E、F在直线AB的同侧(如图1所示)
①若∠COF=25°,求∠BOE的度数.
②若∠COF=α°,则∠BOE=????????? °.
(2)当点C与点E、F在直线AB的两旁(如图2所示)时,(1)中第②式的结论是否仍然成立?请给出你的结论并说明理由.
参考答案
一、选择题
1、B
2、B
3、60,
4、C
5、?B
6、D
7、C;
8、B
9、?B
10、C
二、填空题
11、
12、?100
13、50
14、30
15、南偏东25°
16、50°
17、110°
18、30°;
三、作图题
19、
20、思路解析:可利用本节所学知识,也可以利用其他方法.
答案:方法一:将∠AOB折叠,使射线OA、OB重合,再以O为端点,在∠AOB的内部沿折痕画一条射线,即为∠AOB的平分线;
方法二:用量角器先量出∠AOB的大小,再以OA或OB为一边作一个角等于∠AOB的一半,这个角的另一边即为∠AOB的平分线.
四、计算题
21、360°÷7
=51°+3°÷7
=51°+25′+5′÷7
=51°+25′+300″÷7
≈51°+25′+43″
≈51°26′.
22、解法一? 132°26′42″-41.325°×3
=132.445°-123.975°
=8.47°.
解法二? 132°26′42″-41.325°×3
=132°26′42″-123.975°
=132°26′42″-123°58′30″
=131°86′42″-123°58′30″
=8°28′12″.
23、
24、解:设∠AOC的度数为,根据题意得:
解之:=6?? 答:(略)
五、简答题
25、∵OE平分∠BOD,∴∠BOD=2∠BOE=217°18′=34°36′(2分)
又∵∠AOC+∠AOB+∠DOC+∠BOD=360°且OA⊥OB,OC⊥OD
即∠AOB=∠DOC=90°,∴∠AOC+∠BOD=180°(4分)
∠AOC=180°-34°36′=145°24′(6分)
26、解:(1)如图,
,
(2)的大小不变,理由是:
(3)的大小发生变化情况为, 如图3,则为45°;如图4,则为135度.
27、(1)①∠BOF=∠EOC;???????? ②∠BOP=∠COP.
(2) ①对顶角相等,? 40.???? ②∠BOC? 20???? ③500
28、(1)9;
(2)65°,65°;
(3)结论:OE平分∠BOC.
理由:设∠AOC=2α,
∵OD平分∠AOC,∠AOC =2α,
∴∠AOD=∠COD ==α,
又∵∠DOE=90°
∴∠COE =∠DOE-∠COD =90°-α.
又∵∠BOE =180°-∠DOE-∠AOD=180°-90°-α=90°-α,
∴∠COE=∠BOE,即OE平分∠BOC.
29、解:由题意可知,∠AOE=180°
又∵;∴∠BOD=90°
又∵平分
∴∠BOC=∠BOD=45°
又∵,∴∠1=46°
∴=∠AOB+∠BOC=46°+45°=91°
30、解:(1)9?
(2)155°
(3)平分
31、(1)①∠BOE=50°? ②∠BOE=2α°
(2)当点C与点E、F在直线AB的两旁时,第②式的结论仍然成立,
