24.5与圆有关的位置关系复习
文档属性
| 名称 | 24.5与圆有关的位置关系复习 |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-30 23:32:38 | ||
图片预览





文档简介
课件32张PPT。 与圆有关的位置关系复 习 课学习目标1.掌握点与圆、直线与圆、圆和圆
的位置关系,掌握切线的概念、掌
握切线与过切点的半径之间的位置
关系,会判断一条直线是否为圆的切线,掌握三
角形的内心与外心。
2.结合相关图形的探索与证明,进一步培养的合情
推理能力,发展逻辑思维能力和推理论证的表达
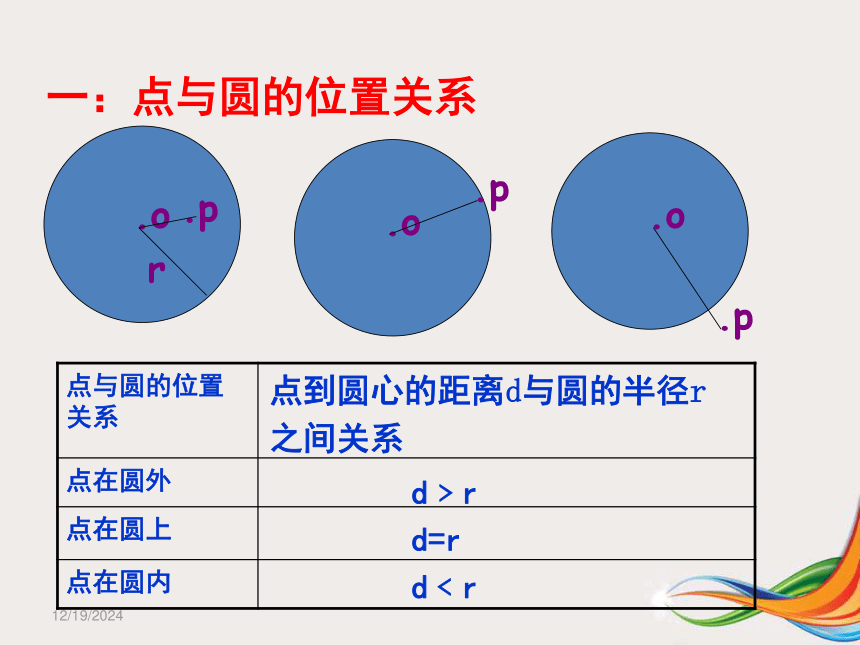
能力。本单元知识结构图:点和圆的位置关系直线与圆的位置关系圆和圆的位置关系三角形外接圆三角形内切圆与圆有关的位置关系判断关键:距离与半径相比较数形结合: 位置关系 数量关系 1/23/2019一:点与圆的位置关系d﹥rd=rd﹤r点到圆心的距离d与圆的半径r
之间关系
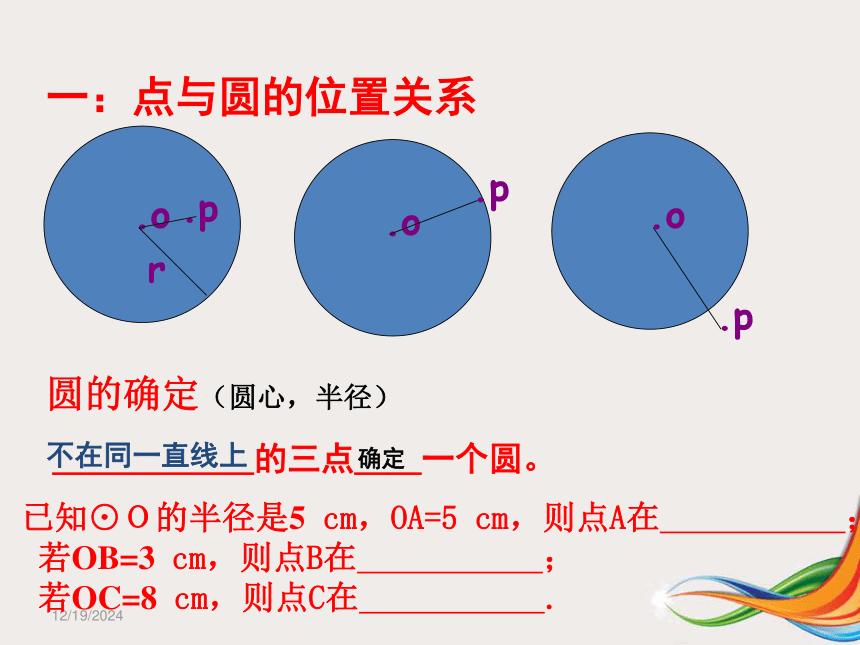
1/23/2019一:点与圆的位置关系圆的确定(圆心,半径)______的三点__一个圆。不在同一直线上确定已知⊙O的半径是5 cm,OA=5 cm,则点A在 ;
若OB=3 cm,则点B在 ;
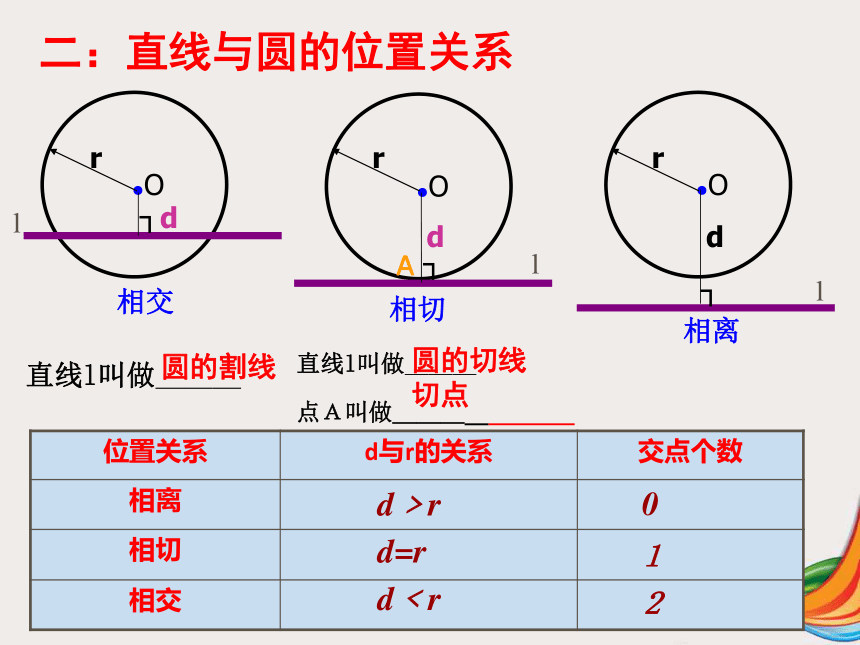
若OC=8 cm,则点C在 .1/23/2019二:直线与圆的位置关系lllA直线l叫做___ 直线l叫做___
点A叫做___ d﹥rd=rd﹤r012圆的割线圆的切线
切点1/23/2019切线的判定与性质(一)切线的判定方法距离
法
判定
定理圆心到直线的距离等于
圆的半径,则此直线是
圆的切线过半径的外端且垂直于
半径的直线是圆的切线若0A⊥CD于A,且OA=r.则CD是⊙O
的切线交点A明确:
连OA,证OA⊥CD即可交点A不明确:
作OA⊥CD于A,证OA=r即可(二)切线的性质
若0A是⊙O的半径,
且0A⊥CD则CD是⊙O
的切线.性质定理:圆的切线垂直于经过切点
的半径.
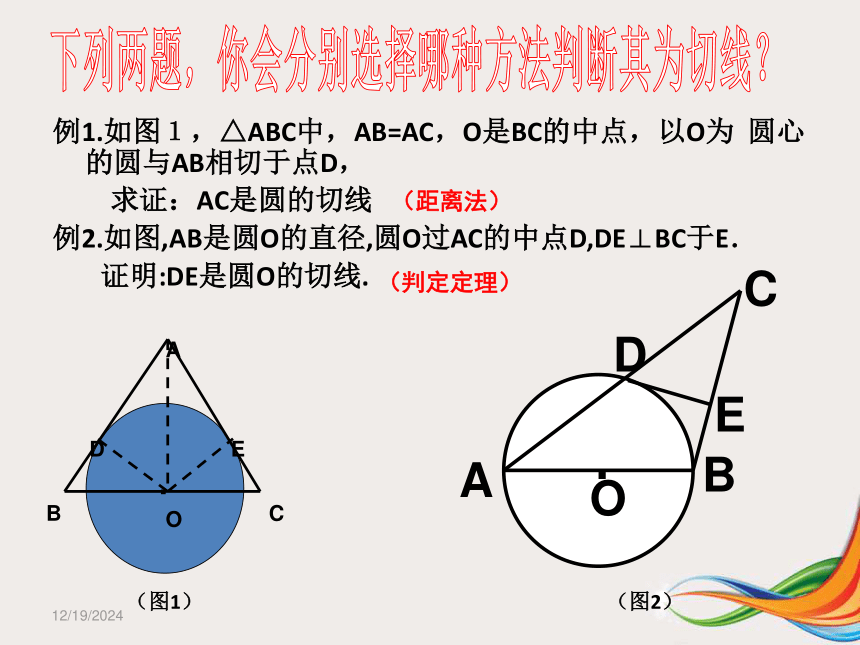
1/23/2019例1.如图1,△ABC中,AB=AC,O是BC的中点,以O为 圆心的圆与AB相切于点D,
求证:AC是圆的切线
例2.如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
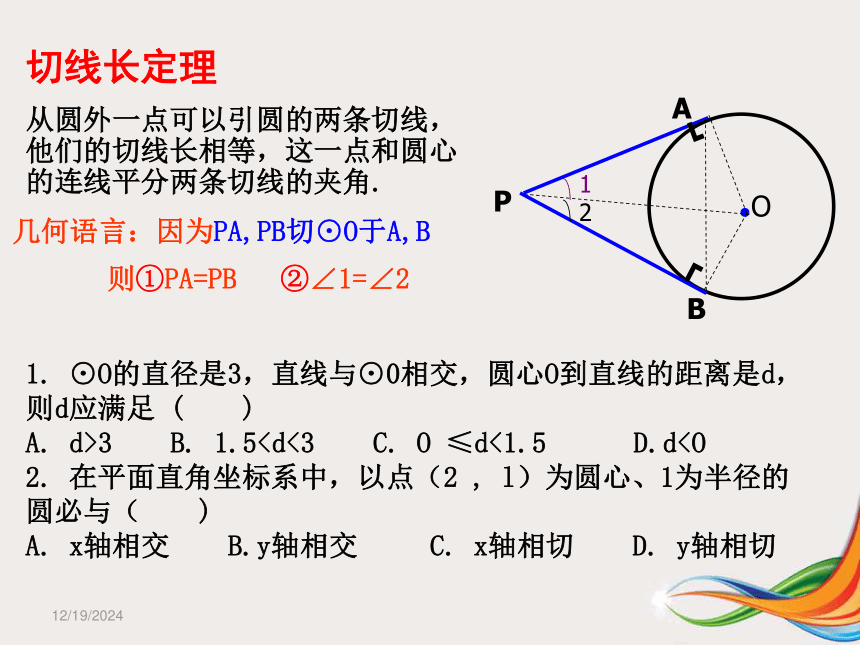
下列两题,你会分别选择哪种方法判断其为切线?(距离法)(判定定理)1/23/2019从圆外一点可以引圆的两条切线,他们的切线长相等,这一点和圆心的连线平分两条切线的夹角.切线长定理几何语言:因为PA,PB切⊙O于A,B 则①PA=PB ②∠1=∠21. ⊙O的直径是3,直线与⊙0相交,圆心O到直线的距离是d,
则d应满足 ( )
A. d>3 B. 1.52. 在平面直角坐标系中,以点(2 , l)为圆心、1为半径的
圆必与( )
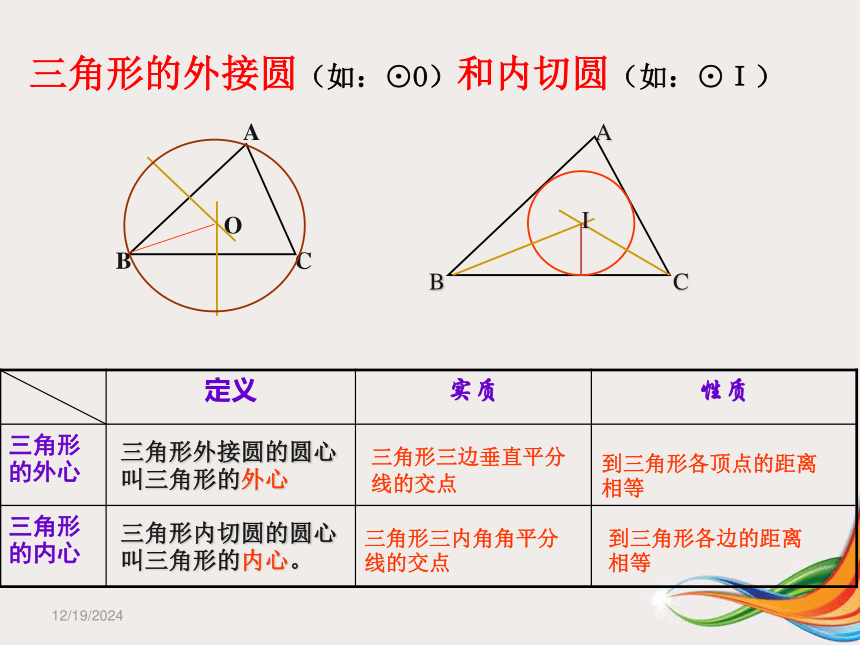
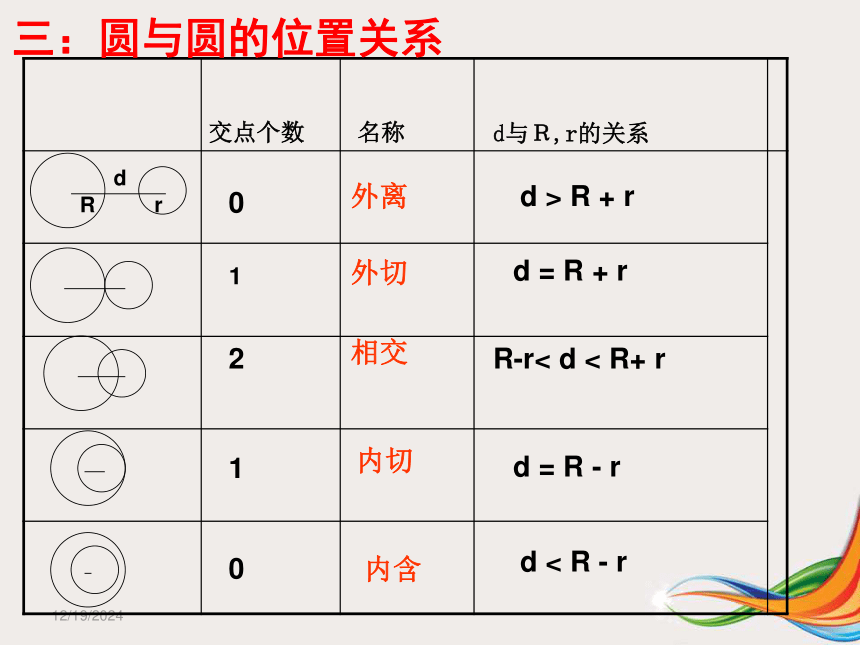
A. x轴相交 B.y轴相交 C. x轴相切 D. y轴相切1/23/2019三角形的外接圆(如:⊙O)和内切圆(如:⊙I) 三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等1/23/2019交点个数 名称d与R,r的关系三:圆与圆的位置关系
1/23/2019三:圆与圆的位置关系
在图中有两圆的多种位置关系,请你指出没有的位置关系是 .相 交1/23/2019
1.有两个同心圆,圆心为O,半径分别为8和5,P是圆环内一点,则OP的取值范围是____.
2.已知⊙O和⊙P的半径分别为5和2,OP=3,则⊙O和⊙P的位置 关系是( )
A、外离 B、外切 C、相交 D、内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,则另一个圆的半径为________.
4.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
出手小试5<OP <8D4cm或16cmD已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.分析:要证DC是⊙O的切线,需证DC垂直于过切点的直径或半径,因此要作辅助线半径OD,利用平行关系推出∠3=∠4,又因为OD=OB,OC为公共边,因此△CDO≌△CBO,所以∠ODC=∠OBC=90°.
证明:连结OD.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3,∠2=∠4.
∴∠3=∠4.
∵OD=OB,OC=OC,
∴△ODC≌△OBC.
∴∠ODC=∠OBC.
∵BC是⊙O的切线,
∴∠OBC=90°.
∴∠ODC=90°.
∴DC是⊙O的切线.BDO124CA3探究 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10(O)探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BACO10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BACO10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB②当圆心O在_____上时BCO探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB②当圆心O在_____上时BCO探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切? 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在AB上时作OD⊥ AC于D ②当圆心O在BC上时当 OD=r= 时⊙O与 AC相切 在 Rt△AOD中∠ A=60°∴ ∠ AOD=30° 设AD=x , AO=2AD=2x 即得x=1 ∴AD=1 , AO=2 ∴BO=8 ∴t=8 2=4s时,⊙O与 AC相切 BACODX2X10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切? 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在AB上时作OD⊥ AC于D ②当圆心O在BC上时∵ OD=r= 时⊙O与 AC相切 ∵ Rt△AOD中∠ A=60°∴ ∠ AOD=30° 设AD=x , AO=2AD=2x 即得x=1 ∴AD=1 , AO=2 ∴BO=8 ∴t=8 2=4s时,⊙O与 AC相切 作OE⊥ AC于E ∵ OE=r= 时⊙O与 AC相切 此时,得CO=AO=2 ∴t=22 2=11s时,⊙O与 AC相切 点O移动距离为22 ∴t = 4s 或 11s 时, ⊙O与 AC相切 BAC10OEX2XDO1/23/2019小结1.知识:掌握“与圆有关的位置关系”中相关的概念,性质与判定.2.思想方法:数形结合,类比,分类讨论,方程思想.面积法作业学业水平:100——103页下课啦!!
的位置关系,掌握切线的概念、掌
握切线与过切点的半径之间的位置
关系,会判断一条直线是否为圆的切线,掌握三
角形的内心与外心。
2.结合相关图形的探索与证明,进一步培养的合情
推理能力,发展逻辑思维能力和推理论证的表达
能力。本单元知识结构图:点和圆的位置关系直线与圆的位置关系圆和圆的位置关系三角形外接圆三角形内切圆与圆有关的位置关系判断关键:距离与半径相比较数形结合: 位置关系 数量关系 1/23/2019一:点与圆的位置关系d﹥rd=rd﹤r点到圆心的距离d与圆的半径r
之间关系
1/23/2019一:点与圆的位置关系圆的确定(圆心,半径)______的三点__一个圆。不在同一直线上确定已知⊙O的半径是5 cm,OA=5 cm,则点A在 ;
若OB=3 cm,则点B在 ;
若OC=8 cm,则点C在 .1/23/2019二:直线与圆的位置关系lllA直线l叫做___ 直线l叫做___
点A叫做___ d﹥rd=rd﹤r012圆的割线圆的切线
切点1/23/2019切线的判定与性质(一)切线的判定方法距离
法
判定
定理圆心到直线的距离等于
圆的半径,则此直线是
圆的切线过半径的外端且垂直于
半径的直线是圆的切线若0A⊥CD于A,且OA=r.则CD是⊙O
的切线交点A明确:
连OA,证OA⊥CD即可交点A不明确:
作OA⊥CD于A,证OA=r即可(二)切线的性质
若0A是⊙O的半径,
且0A⊥CD则CD是⊙O
的切线.性质定理:圆的切线垂直于经过切点
的半径.
1/23/2019例1.如图1,△ABC中,AB=AC,O是BC的中点,以O为 圆心的圆与AB相切于点D,
求证:AC是圆的切线
例2.如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
下列两题,你会分别选择哪种方法判断其为切线?(距离法)(判定定理)1/23/2019从圆外一点可以引圆的两条切线,他们的切线长相等,这一点和圆心的连线平分两条切线的夹角.切线长定理几何语言:因为PA,PB切⊙O于A,B 则①PA=PB ②∠1=∠21. ⊙O的直径是3,直线与⊙0相交,圆心O到直线的距离是d,
则d应满足 ( )
A. d>3 B. 1.5
圆必与( )
A. x轴相交 B.y轴相交 C. x轴相切 D. y轴相切1/23/2019三角形的外接圆(如:⊙O)和内切圆(如:⊙I) 三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等1/23/2019交点个数 名称d与R,r的关系三:圆与圆的位置关系
1/23/2019三:圆与圆的位置关系
在图中有两圆的多种位置关系,请你指出没有的位置关系是 .相 交1/23/2019
1.有两个同心圆,圆心为O,半径分别为8和5,P是圆环内一点,则OP的取值范围是____.
2.已知⊙O和⊙P的半径分别为5和2,OP=3,则⊙O和⊙P的位置 关系是( )
A、外离 B、外切 C、相交 D、内切
3.两圆相切,圆心距为10cm,其中一个圆的半径为6cm,则另一个圆的半径为________.
4.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切或相交
出手小试5<OP <8D4cm或16cmD已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.分析:要证DC是⊙O的切线,需证DC垂直于过切点的直径或半径,因此要作辅助线半径OD,利用平行关系推出∠3=∠4,又因为OD=OB,OC为公共边,因此△CDO≌△CBO,所以∠ODC=∠OBC=90°.
证明:连结OD.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3,∠2=∠4.
∴∠3=∠4.
∵OD=OB,OC=OC,
∴△ODC≌△OBC.
∴∠ODC=∠OBC.
∵BC是⊙O的切线,
∴∠OBC=90°.
∴∠ODC=90°.
∴DC是⊙O的切线.BDO124CA3探究 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10(O)探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BACO10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BACO10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10O探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB②当圆心O在_____上时BCO探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切?BAC10 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在_____上时AB②当圆心O在_____上时BCO探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切? 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在AB上时作OD⊥ AC于D ②当圆心O在BC上时当 OD=r= 时⊙O与 AC相切 在 Rt△AOD中∠ A=60°∴ ∠ AOD=30° 设AD=x , AO=2AD=2x 即得x=1 ∴AD=1 , AO=2 ∴BO=8 ∴t=8 2=4s时,⊙O与 AC相切 BACODX2X10探究1 如图, ⊙O的半径为 cm,正三角形的边长为10 cm,
圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动,设运动时间为
t(s)
问: (1) 在移动过程中, ⊙O与△ABC 的三条边相切几次?
(2) t为何值时, ⊙O与 AC相切? 解(1) 在移动过程中, ⊙O与△ABC 的三条边相切6次。 (2)① 当圆心O在AB上时作OD⊥ AC于D ②当圆心O在BC上时∵ OD=r= 时⊙O与 AC相切 ∵ Rt△AOD中∠ A=60°∴ ∠ AOD=30° 设AD=x , AO=2AD=2x 即得x=1 ∴AD=1 , AO=2 ∴BO=8 ∴t=8 2=4s时,⊙O与 AC相切 作OE⊥ AC于E ∵ OE=r= 时⊙O与 AC相切 此时,得CO=AO=2 ∴t=22 2=11s时,⊙O与 AC相切 点O移动距离为22 ∴t = 4s 或 11s 时, ⊙O与 AC相切 BAC10OEX2XDO1/23/2019小结1.知识:掌握“与圆有关的位置关系”中相关的概念,性质与判定.2.思想方法:数形结合,类比,分类讨论,方程思想.面积法作业学业水平:100——103页下课啦!!
同课章节目录
