人教A版(2019)选择性必修第三册7.5正态分布同步练习(word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册7.5正态分布同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 653.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 19:02:46 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 7.5 正态分布 同步练习
一、单选题
1.某工厂生产了根钢管,其钢管内径(单位:)服从正态分布,工作人员通过抽样的方式统计出,钢管内径高于的占钢管总数的,则这批钢管内径在到之间的钢管根数约为( )
A. B. C. D.
2.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
3.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)=( )
A.0.158 8 B.0.158 65 C.0.158 6 D.0.158 5
4.已知随机变量服从正态分布,且,则( )
A. B. C. D.
5.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
6.已知随机变量,,且,,则( )
A. B. C. D.
7.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
8.已知随机变量服从二项分布,其期望,随机变量服从正态分布,若,则( )
A. B. C. D.
9.已知随机变量,若,则( )
A. B. C. D.
10.已知随机变量,且,,则为( )
A.0.1358 B.0.1359 C.0.2716 D.0.2718
11.某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为( )
A.10 B.9 C.8 D.7
12.已知,且,则( )
A.0.3 B.0.4 C.0.85 D.0.7
13.2020年8月11日,国家主席习近平同志对制止餐饮浪费行为作出重要指示,他指出,餐饮浪费现象,触目惊心,令人痛心!“谁知盘中餐,粒粒皆辛苦”,某中学制订了“光盘计划”,面向该校师生开展了一次问卷调查,目的是了解师生们对这一倡议的关注度和支持度,得到参与问卷调查中的2000人的得分数据.据统计此次问卷调查的得分(满分:100分)服从正态分布,则( )
若随机变量,则,
A.0.34135 B.0.8186 C.0.6827 D.0.47725
14.某校团委决定举办“鉴史知来”读书活动,经过选拔,共10名同学的作品被选为优秀作品,其中高一年级5名同学,高二年级5名同学,现从这10个优秀作品中随机抽7个,则高二年级5名同学的作品全被抽出的概率为( )
A. B. C. D.
15.设随机变量,则( )
A.0 B.1 C. D.
二、填空题
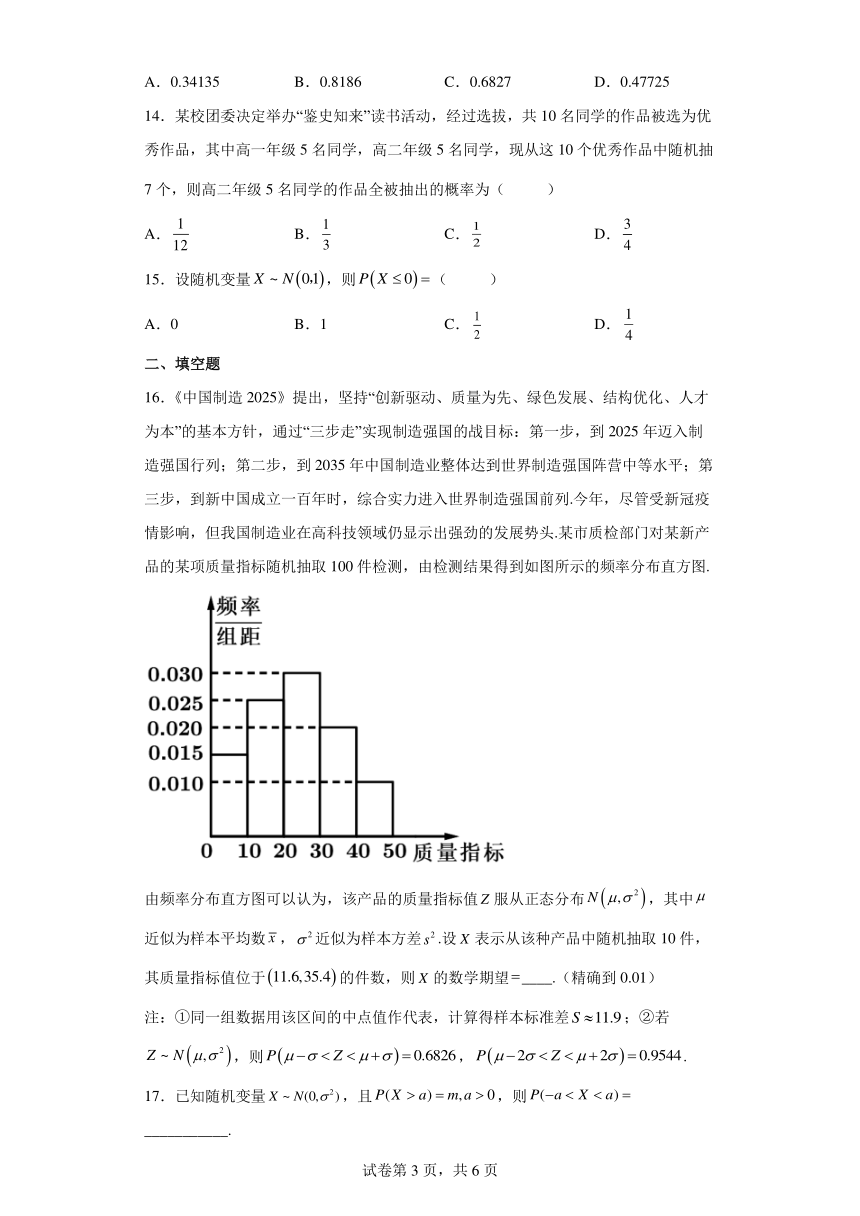
16.《中国制造2025》提出,坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,通过“三步走”实现制造强国的战目标:第一步,到2025年迈入制造强国行列;第二步,到2035年中国制造业整体达到世界制造强国阵营中等水平;第三步,到新中国成立一百年时,综合实力进入世界制造强国前列.今年,尽管受新冠疫情影响,但我国制造业在高科技领域仍显示出强劲的发展势头.某市质检部门对某新产品的某项质量指标随机抽取100件检测,由检测结果得到如图所示的频率分布直方图.
由频率分布直方图可以认为,该产品的质量指标值服从正态分布,其中近似为样本平均数,近似为样本方差.设表示从该种产品中随机抽取10件,其质量指标值位于的件数,则的数学期望____.(精确到0.01)
注:①同一组数据用该区间的中点值作代表,计算得样本标准差;②若,则,.
17.已知随机变量,且,则___________.
18.若随机变量,则服从的正态分布为______(填序号).
①;②;③;④.
三、解答题
19.为了严格监控某种零件的一条生产线的生产过程,某企业每天从该生产线上随机抽取10000个零件,并测量其内径(单位:).根据长期生产经验,认为这条生产线正常状态下生产的零件的内径服从正态分布.如果加工的零件内径小于或大于均为不合格品,其余为合格品.
(1)假设生产状态正常,请估计一天内抽取的10000个零件中不合格品的个数约为多少;
(2)若生产的某件产品为合格品则该件产品盈利;若生产的某件产品为不合格品则该件产品亏损.已知每件产品的利润(单位:元)与零件的内径有如下关系:.求该企业一天从生产线上随机抽取10000个零件的平均利润.
附:若随机变量服从正态分布,有,,.
20.2021年3月24日,某些国际服装企业因抵制新疆棉花声明在中国互联网上引发热议.对此,中国外交部发言人25日表示,中国光明磊落,中国人民友善开放,但中国民意不可欺 不可违.某记者随机采访了100名群众,调查群众对此事件的看法,根据统计,抽取的100名群众的年龄频率分布直方图如图所示.
(1)求这100名受访群众年龄的平均数和方差(同一组数据用该区间的中点值代替).
(2)由频率分布直方图可以认为,受访群众的年龄服从正态分布,其中近似为,近似为.
①求;
②从年龄在,的受访群众中,按分层抽样的方法,抽出7人参加访谈节目录制,再从这7人中随机抽出3人作为代表发言,设这3位发言人的年龄落在内的人数为,求变量的分布列和数学期望.
参考数据:取,若,则,.
21.在一次大范围的随机知识问卷调查中,通过随机抽样,得到参加问卷调查的100人的得分统计结果如下表所示:
得分
频数 2 13 21 25 24 11 4
(1)由频数分布表可以大致认为,此次问卷调查的得分,近似为这100人得分的平均值(同一组中的数据用该组区间的左端点值作代表).
①求的值;
②若,求的值;
(2)在(1)的条件下,为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于的可以获赠2次随机话费,得分低于的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) 20 50
概率
现有市民甲参加此次问卷调查,记(单位:元)为该市民参加问卷调查获赠的话费,求的分布列与数学期望.
22.为保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设某高校为了解全校学生的阅读情况,随机调查了200名学生的每周阅读时间x(单位:小时)并绘制如图所示的频率分布直方图:
(1)求这200名学生每周阅读时间的样本平均数和样本方差(同一组的数据用该组区间中点值代表);
(2)由直方图可以看出,目前该校学生每周的阅读时间x大致服从正态分布,其中近似为样本平均数,近似为样本方差.
①一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若,令,则,且利用直方图得到的正态分布,求;
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求Z的均值.
参考数据:,若,则.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
利用正态分布的特征,求出即可计算出这批钢管内径在到之间的钢管根数.
【详解】
,,故这批钢管内径在到之间的钢管数约为根.
故选:C
正态分布的问题通常利用正态曲线的特点解题:
(1)对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
(2)均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。
关于μ对称,并在μ处取最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点,形状呈现中间高两边低,正态分布的概率密度函数曲线呈钟形。
2.A
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
3.B
根据题意可得,得出答案.
【详解】
随机变量X服从正态分布N(3,1),其图象的对称轴为X = 3.
所以
所以
故选:B
本题考查根据正态分布曲线的对称性求对应的概率,属于基础题.
4.A
利用对称性结合,求得,再由 求解.
【详解】
因为随机变量服从正态分布,
由对称性可知,,
又,
所以,
故.
故选:A.
5.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
6.B
根据随机变量可知,再根据,,可求出,利用,建立方程,即可求出结果.
【详解】
因为随机变量,所以,
因为,,所以,即,
又
所以,即.
故选:B.
7.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
8.D
由得到p,根据正态分布的性质再由得到及可得答案.
【详解】
由,则,则,则,
故选:D.
本题考查二项分布的期望与正态分布的概率,属于基础题 。
9.B
利用正态密度曲线的对称性可得出,即可得解.
【详解】
因为随机变量,则.
故选:B.
10.B
由随机变量可知,利用正态分布的对称性求解即可
【详解】
由随机变量知,,
所以,,
所以,
故选:B
11.B
由,根据对称性得出,由此求得该班学生数学成绩在120分以上的概率,问题得解.
【详解】
因为数学成绩,
所以由可得:,
所以该班学生数学成绩在120分以上的概率为:,
所以估计该班学生数学成绩在120分以上的人数为:(人)
故答案为:9.
本题考查正态曲线的特点及曲线所表示的意义,是一个基础题,解题的关键是考试的成绩的概率分布关于对称,利用对称写出要用的一段分数的概率,题目得解.
12.D
根据正态分布的性质计算可得;
【详解】
解:因为,正态曲线的对称轴为,因为,所以,所以
故选:D
13.B
根据正态分布的对称性与原则求解即可.
【详解】
解:因为得分(满分:100分)服从正态分布,
所以,
所以
故选:B
14.A
用表示抽到高二年级同学的作品数,,即可得到答案.
【详解】
从10个作品中抽7个,用表示抽到高二年级同学的作品数,
则.
故选:A.
15.C
根据正态分布曲线的对称性得结论.
【详解】
因为随机变量,所以正态曲线关于对称,所以.
16.6.83
计算,由所给条件判断,从而得到的概率,由抽取每一件的概率抽取10件的期望值.
【详解】
计算得,
由条件,从而.
故从该种产品中随机抽取1件,其质量指标值位于的概率是0.6826,
所以抽取10件的期望值为:所以.
故答案为:.
17.
根据正态分布区间的对称性直接计算即可.
【详解】
由,且
则,所以
故答案为:
18.④
根据变量线性变化后,其均值、方差的变化情况判断.
【详解】
∵,,
∴,,故.故④正确.
故答案为:④
19.(1)26;(2)元.
(1)根据正态分布的原则,零件的尺寸在之内的概率为,从而可得不合格品的概率为,即可求解.
(2)根据正态分布的原则,求出对应的概率,再利用均值的计算公式即可求解.
【详解】
(1)抽取的一个零件的尺寸在之内的概率为,
从而抽取一个零件为不合格品的概率为,
因此一天内抽取的10000个零件中不合格品的个数约为:.
(2)结合正态分布曲线和题意可知:
,
,
,
,
故随机抽取10000个零件的平均利润:
元.
本题考查了正态分布曲线的性质以及应用、正态分布期望的求法、原则的综合应用,属于中档题.
20.(1),;(2)①;②分布列答案见解析,数学期望:.
(1)根据同一组数据用该区间的中点值代替,结合平均数的公式、方差的公式进行运算即可;
(2)①:根据正态分布的对称性,结合题中所给的概率公式及数据进行求解即可;
②:根据分层抽样的性质求出的可能取值,求出每种可能的概率,写出分布列、计算出数学期望即可.
【详解】
解:(1),
.
(2)①由(1)知,
所以.
②分层抽样抽取的7人中年龄在,内的分别有3人,4人.
所以的可能取值为0,1,2,3.
因为,,,,
所以的分布列为
0 1 2 3
故的数学期望.
21.(1)①;②;(2)分布列答案见解析,数学期望为41.25元.
(1)根据题意直接计算平均值即可,再结合正态分布的对称性得到,即得a值;
(2)先根据正态分布知获赠1次和2次随机话费的概率均为,再结合获得随机话费的金额和概率情况写分布列,并计算期望即可.
【详解】
解:(1)①由题意得:,
,
②,
由正态分布曲线的对称性得,,
解得;
(2)由题意得,,即获赠1次和2次随机话费的概率均为,
故获赠话费的的所有可能取值为20,40,50,70,100
,
,
,
,
.
的分布列为:
20 40 50 70 100
元.
所以的数学期望为41.25元.
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列;
(3)根据期望的概念,结合分布列,即可得出期望(在计算时,要注意随机变量是否服从特殊的分布,如超几何分布或二项分布等,可结合其对应的概率计算公式及期望计算公式,简化计算).
22.(1),;
(2)①;②.
(1)利用频率分布直方图计算平均数和方差的方法直接计算作答.
(2)①利用给定公式直接计算;②利用①的结论结合二项分布的期望公式计算作答.
(1)
根据频率分布直方图知,阅读时间在区间
内的频率分别为,
,
,
所以样本平均数和样本方差分别为9,1.78.
(2)
①由题意知,,则有,
,,
②由①知,可得,
所以Z的均值.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某工厂生产了根钢管,其钢管内径(单位:)服从正态分布,工作人员通过抽样的方式统计出,钢管内径高于的占钢管总数的,则这批钢管内径在到之间的钢管根数约为( )
A. B. C. D.
2.王老师为了了解全班50位同学某次考试的成绩状况,随机抽查了10位同学该次考试的数学与物理成绩,列表如下:
学生 甲 乙 丙 丁 戊 己 庚 辛 壬 癸 平均值 标准差
数学成绩X/分 88 62
物理成绩Y/分 75 63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩的正态曲线,虚线表示全班物理成绩的正态曲线,则随机变量与的正态曲线可能是( )A. B.
C. D.
3.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)=( )
A.0.158 8 B.0.158 65 C.0.158 6 D.0.158 5
4.已知随机变量服从正态分布,且,则( )
A. B. C. D.
5.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
6.已知随机变量,,且,,则( )
A. B. C. D.
7.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
8.已知随机变量服从二项分布,其期望,随机变量服从正态分布,若,则( )
A. B. C. D.
9.已知随机变量,若,则( )
A. B. C. D.
10.已知随机变量,且,,则为( )
A.0.1358 B.0.1359 C.0.2716 D.0.2718
11.某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为( )
A.10 B.9 C.8 D.7
12.已知,且,则( )
A.0.3 B.0.4 C.0.85 D.0.7
13.2020年8月11日,国家主席习近平同志对制止餐饮浪费行为作出重要指示,他指出,餐饮浪费现象,触目惊心,令人痛心!“谁知盘中餐,粒粒皆辛苦”,某中学制订了“光盘计划”,面向该校师生开展了一次问卷调查,目的是了解师生们对这一倡议的关注度和支持度,得到参与问卷调查中的2000人的得分数据.据统计此次问卷调查的得分(满分:100分)服从正态分布,则( )
若随机变量,则,
A.0.34135 B.0.8186 C.0.6827 D.0.47725
14.某校团委决定举办“鉴史知来”读书活动,经过选拔,共10名同学的作品被选为优秀作品,其中高一年级5名同学,高二年级5名同学,现从这10个优秀作品中随机抽7个,则高二年级5名同学的作品全被抽出的概率为( )
A. B. C. D.
15.设随机变量,则( )
A.0 B.1 C. D.
二、填空题
16.《中国制造2025》提出,坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,通过“三步走”实现制造强国的战目标:第一步,到2025年迈入制造强国行列;第二步,到2035年中国制造业整体达到世界制造强国阵营中等水平;第三步,到新中国成立一百年时,综合实力进入世界制造强国前列.今年,尽管受新冠疫情影响,但我国制造业在高科技领域仍显示出强劲的发展势头.某市质检部门对某新产品的某项质量指标随机抽取100件检测,由检测结果得到如图所示的频率分布直方图.
由频率分布直方图可以认为,该产品的质量指标值服从正态分布,其中近似为样本平均数,近似为样本方差.设表示从该种产品中随机抽取10件,其质量指标值位于的件数,则的数学期望____.(精确到0.01)
注:①同一组数据用该区间的中点值作代表,计算得样本标准差;②若,则,.
17.已知随机变量,且,则___________.
18.若随机变量,则服从的正态分布为______(填序号).
①;②;③;④.
三、解答题
19.为了严格监控某种零件的一条生产线的生产过程,某企业每天从该生产线上随机抽取10000个零件,并测量其内径(单位:).根据长期生产经验,认为这条生产线正常状态下生产的零件的内径服从正态分布.如果加工的零件内径小于或大于均为不合格品,其余为合格品.
(1)假设生产状态正常,请估计一天内抽取的10000个零件中不合格品的个数约为多少;
(2)若生产的某件产品为合格品则该件产品盈利;若生产的某件产品为不合格品则该件产品亏损.已知每件产品的利润(单位:元)与零件的内径有如下关系:.求该企业一天从生产线上随机抽取10000个零件的平均利润.
附:若随机变量服从正态分布,有,,.
20.2021年3月24日,某些国际服装企业因抵制新疆棉花声明在中国互联网上引发热议.对此,中国外交部发言人25日表示,中国光明磊落,中国人民友善开放,但中国民意不可欺 不可违.某记者随机采访了100名群众,调查群众对此事件的看法,根据统计,抽取的100名群众的年龄频率分布直方图如图所示.
(1)求这100名受访群众年龄的平均数和方差(同一组数据用该区间的中点值代替).
(2)由频率分布直方图可以认为,受访群众的年龄服从正态分布,其中近似为,近似为.
①求;
②从年龄在,的受访群众中,按分层抽样的方法,抽出7人参加访谈节目录制,再从这7人中随机抽出3人作为代表发言,设这3位发言人的年龄落在内的人数为,求变量的分布列和数学期望.
参考数据:取,若,则,.
21.在一次大范围的随机知识问卷调查中,通过随机抽样,得到参加问卷调查的100人的得分统计结果如下表所示:
得分
频数 2 13 21 25 24 11 4
(1)由频数分布表可以大致认为,此次问卷调查的得分,近似为这100人得分的平均值(同一组中的数据用该组区间的左端点值作代表).
①求的值;
②若,求的值;
(2)在(1)的条件下,为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于的可以获赠2次随机话费,得分低于的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) 20 50
概率
现有市民甲参加此次问卷调查,记(单位:元)为该市民参加问卷调查获赠的话费,求的分布列与数学期望.
22.为保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设某高校为了解全校学生的阅读情况,随机调查了200名学生的每周阅读时间x(单位:小时)并绘制如图所示的频率分布直方图:
(1)求这200名学生每周阅读时间的样本平均数和样本方差(同一组的数据用该组区间中点值代表);
(2)由直方图可以看出,目前该校学生每周的阅读时间x大致服从正态分布,其中近似为样本平均数,近似为样本方差.
①一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若,令,则,且利用直方图得到的正态分布,求;
②从该高校的学生中随机抽取20名,记Z表示这20名学生中每周阅读时间超过10小时的人数,求Z的均值.
参考数据:,若,则.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
利用正态分布的特征,求出即可计算出这批钢管内径在到之间的钢管根数.
【详解】
,,故这批钢管内径在到之间的钢管数约为根.
故选:C
正态分布的问题通常利用正态曲线的特点解题:
(1)对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
(2)均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。
关于μ对称,并在μ处取最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点,形状呈现中间高两边低,正态分布的概率密度函数曲线呈钟形。
2.A
根据、的大小关系可得对称轴的位置关系,根据、可得图象的瘦高、矮胖,进而可得正确选项.
【详解】
因为,所以随机变量的正态曲线的对称轴在随机变量的正态曲线的对称轴的左边,排除B,C;
因为,所以随机变量的总体分布更离散,正态曲线比随机变量的正态曲线“矮胖”,排除D,
故选:A.
3.B
根据题意可得,得出答案.
【详解】
随机变量X服从正态分布N(3,1),其图象的对称轴为X = 3.
所以
所以
故选:B
本题考查根据正态分布曲线的对称性求对应的概率,属于基础题.
4.A
利用对称性结合,求得,再由 求解.
【详解】
因为随机变量服从正态分布,
由对称性可知,,
又,
所以,
故.
故选:A.
5.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
6.B
根据随机变量可知,再根据,,可求出,利用,建立方程,即可求出结果.
【详解】
因为随机变量,所以,
因为,,所以,即,
又
所以,即.
故选:B.
7.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
8.D
由得到p,根据正态分布的性质再由得到及可得答案.
【详解】
由,则,则,则,
故选:D.
本题考查二项分布的期望与正态分布的概率,属于基础题 。
9.B
利用正态密度曲线的对称性可得出,即可得解.
【详解】
因为随机变量,则.
故选:B.
10.B
由随机变量可知,利用正态分布的对称性求解即可
【详解】
由随机变量知,,
所以,,
所以,
故选:B
11.B
由,根据对称性得出,由此求得该班学生数学成绩在120分以上的概率,问题得解.
【详解】
因为数学成绩,
所以由可得:,
所以该班学生数学成绩在120分以上的概率为:,
所以估计该班学生数学成绩在120分以上的人数为:(人)
故答案为:9.
本题考查正态曲线的特点及曲线所表示的意义,是一个基础题,解题的关键是考试的成绩的概率分布关于对称,利用对称写出要用的一段分数的概率,题目得解.
12.D
根据正态分布的性质计算可得;
【详解】
解:因为,正态曲线的对称轴为,因为,所以,所以
故选:D
13.B
根据正态分布的对称性与原则求解即可.
【详解】
解:因为得分(满分:100分)服从正态分布,
所以,
所以
故选:B
14.A
用表示抽到高二年级同学的作品数,,即可得到答案.
【详解】
从10个作品中抽7个,用表示抽到高二年级同学的作品数,
则.
故选:A.
15.C
根据正态分布曲线的对称性得结论.
【详解】
因为随机变量,所以正态曲线关于对称,所以.
16.6.83
计算,由所给条件判断,从而得到的概率,由抽取每一件的概率抽取10件的期望值.
【详解】
计算得,
由条件,从而.
故从该种产品中随机抽取1件,其质量指标值位于的概率是0.6826,
所以抽取10件的期望值为:所以.
故答案为:.
17.
根据正态分布区间的对称性直接计算即可.
【详解】
由,且
则,所以
故答案为:
18.④
根据变量线性变化后,其均值、方差的变化情况判断.
【详解】
∵,,
∴,,故.故④正确.
故答案为:④
19.(1)26;(2)元.
(1)根据正态分布的原则,零件的尺寸在之内的概率为,从而可得不合格品的概率为,即可求解.
(2)根据正态分布的原则,求出对应的概率,再利用均值的计算公式即可求解.
【详解】
(1)抽取的一个零件的尺寸在之内的概率为,
从而抽取一个零件为不合格品的概率为,
因此一天内抽取的10000个零件中不合格品的个数约为:.
(2)结合正态分布曲线和题意可知:
,
,
,
,
故随机抽取10000个零件的平均利润:
元.
本题考查了正态分布曲线的性质以及应用、正态分布期望的求法、原则的综合应用,属于中档题.
20.(1),;(2)①;②分布列答案见解析,数学期望:.
(1)根据同一组数据用该区间的中点值代替,结合平均数的公式、方差的公式进行运算即可;
(2)①:根据正态分布的对称性,结合题中所给的概率公式及数据进行求解即可;
②:根据分层抽样的性质求出的可能取值,求出每种可能的概率,写出分布列、计算出数学期望即可.
【详解】
解:(1),
.
(2)①由(1)知,
所以.
②分层抽样抽取的7人中年龄在,内的分别有3人,4人.
所以的可能取值为0,1,2,3.
因为,,,,
所以的分布列为
0 1 2 3
故的数学期望.
21.(1)①;②;(2)分布列答案见解析,数学期望为41.25元.
(1)根据题意直接计算平均值即可,再结合正态分布的对称性得到,即得a值;
(2)先根据正态分布知获赠1次和2次随机话费的概率均为,再结合获得随机话费的金额和概率情况写分布列,并计算期望即可.
【详解】
解:(1)①由题意得:,
,
②,
由正态分布曲线的对称性得,,
解得;
(2)由题意得,,即获赠1次和2次随机话费的概率均为,
故获赠话费的的所有可能取值为20,40,50,70,100
,
,
,
,
.
的分布列为:
20 40 50 70 100
元.
所以的数学期望为41.25元.
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列;
(3)根据期望的概念,结合分布列,即可得出期望(在计算时,要注意随机变量是否服从特殊的分布,如超几何分布或二项分布等,可结合其对应的概率计算公式及期望计算公式,简化计算).
22.(1),;
(2)①;②.
(1)利用频率分布直方图计算平均数和方差的方法直接计算作答.
(2)①利用给定公式直接计算;②利用①的结论结合二项分布的期望公式计算作答.
(1)
根据频率分布直方图知,阅读时间在区间
内的频率分别为,
,
,
所以样本平均数和样本方差分别为9,1.78.
(2)
①由题意知,,则有,
,,
②由①知,可得,
所以Z的均值.
答案第1页,共2页
答案第1页,共2页
