人教版八年级下册17.1 勾股定理课件(共29张PPT)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 917.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 10:03:18 | ||
图片预览






文档简介
(共29张PPT)
17.1.1 勾股定理
1.掌握勾股定理.
2.经历勾股定理的探究过程,了解关于勾股定理的一 些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
3.会用勾股定理进行简单的计算.
学习目标
重点:掌握勾股定理.
难点:会用勾股定理进行简单的计算.
重难点
相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系.
新课导入
观察一下,你能从中发现什么数量关系吗
(2)
(3)
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1) 已知a 5,b 12,求c;
(2) 已知a 6,c 10,求b;
(3) 已知c 25,b 15,求a.
a
b
c
预习检测
解:(1)
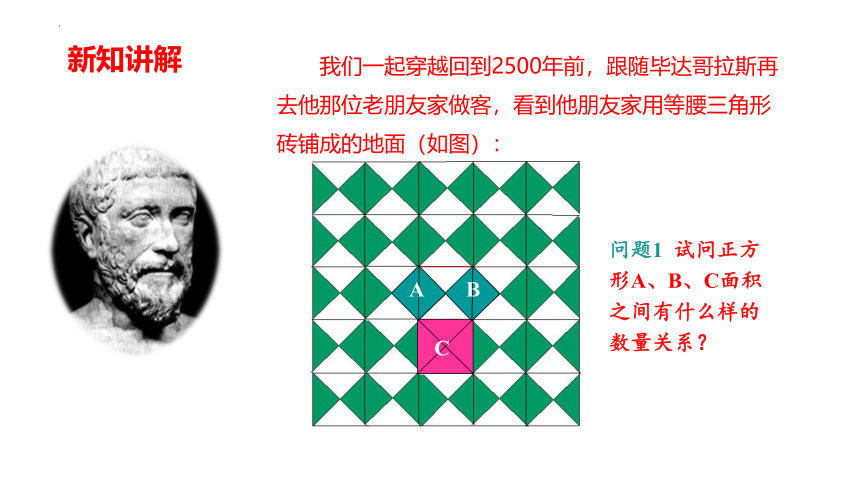
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1 试问正方形A、B、C面积之间有什么样的数量关系?
新知讲解
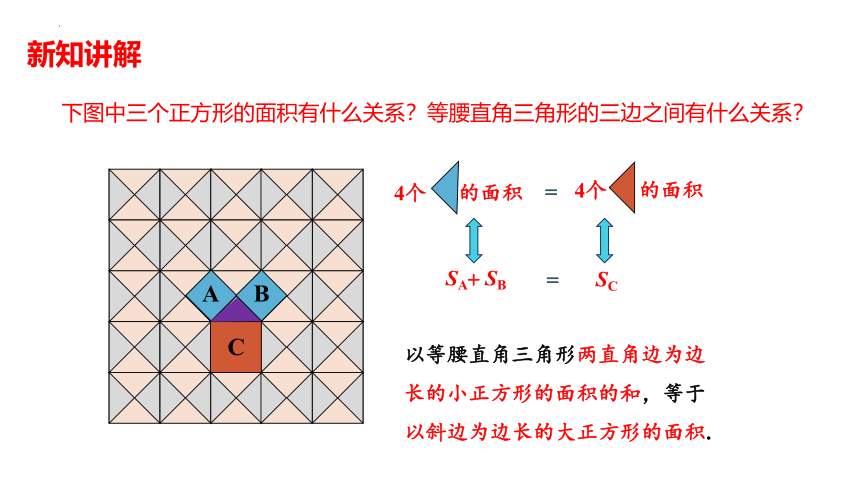
下图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
A
B
C
4个 的面积
4个 的面积
SA SB
SC
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
新知讲解
等腰直角三角形的三边之间有什么关系?
C
SA SB
SC
a
b
c
a b
a
b
c
c
等腰直角三角形斜边的平方等于两直角边的平方和.
其他的直角三角形也有这个性质吗?
A
B
C
新知讲解
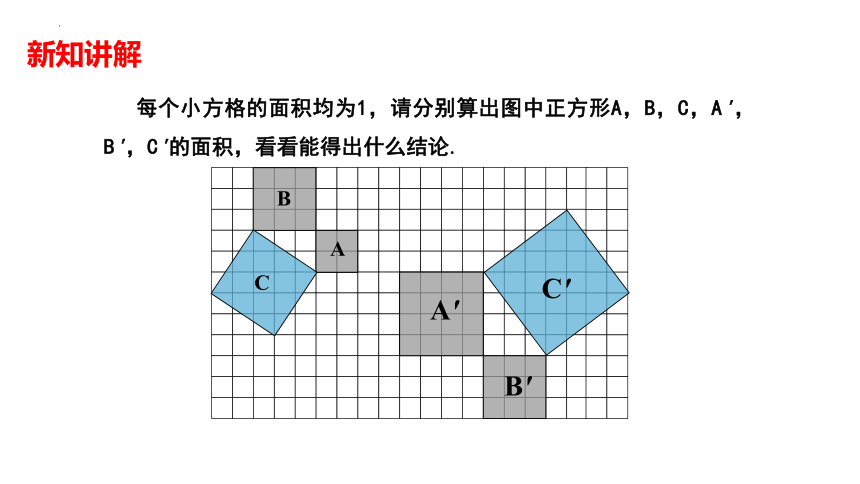
每个小方格的面积均为1,请分别算出图中正方形A,B,C,A',B',C'的面积,看看能得出什么结论.
A
C
B
A'
C'
B'
新知讲解
A
C
B
正方形A的面积
正方形B的面积
正方形C的面积
9个小正方形的面积
9
4
4个小正方形的面积
新知讲解
A
C
B
正方形C的面积 4个直角三角形的面积 小正方形的面积
4 2 3
1
13
割
新知讲解
还有其他的方法吗?
A
C
B
正方形C的面积 大正方形的面积 4个直角三角形的面积
4 2 3
25
13
补
新知讲解
A
C
B
正方形A的面积
正方形B的面积
正方形C的面积
9
4
13
SA SB SC
新知讲解
正方形A'的面积
正方形B'的面积
正方形C'的面积
9
16
25
SA' SB' SC'
A'
C'
B'
新知讲解
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
新知讲解
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子,动手试一试,并证明刚刚的猜想.
a
b
c
a
b
a
b
c
图1
图2
新知讲解
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c .
勾股定理
勾
股
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
股
勾
弦
勾2 股2 弦2
a
b
c
归纳总结
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
例题分析
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得x=
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得x=
巩固练习
∴a=
(2)∵ b=15,∠A=30°
∴a=,c=
C
A
B
a
b
c
例2. 已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴ CD=.
例题分析
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
巩固练习
1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
易错提示
(宁波中考)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
C
链接中考
2.图中阴影部分是一个正方形,则此正方形的面积为__________.
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
8 cm
10 cm
36 cm
随堂检测
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
17
5
74或24
4.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
随堂检测
直角三角形的面积是(cm2).
5. 求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 = 172,
即x2=172-152=289–225=64
∴ x=±8 (负值舍去),
∴另一直角边长为8 cm,
随堂检测
6. 如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
解:∵AE=BE,
∴S△ABE=AE·BE=AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=AB2=;
同理可得S△AHC+S△BCF=.
又∵AC2+BC2=AB2,
∴阴影部分的面积为AB2=.
随堂检测
勾股定理
内容
注意
课堂小结
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
17.1.1 勾股定理
1.掌握勾股定理.
2.经历勾股定理的探究过程,了解关于勾股定理的一 些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
3.会用勾股定理进行简单的计算.
学习目标
重点:掌握勾股定理.
难点:会用勾股定理进行简单的计算.
重难点
相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系.
新课导入
观察一下,你能从中发现什么数量关系吗
(2)
(3)
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1) 已知a 5,b 12,求c;
(2) 已知a 6,c 10,求b;
(3) 已知c 25,b 15,求a.
a
b
c
预习检测
解:(1)
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
A
B
C
问题1 试问正方形A、B、C面积之间有什么样的数量关系?
新知讲解
下图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
A
B
C
4个 的面积
4个 的面积
SA SB
SC
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
新知讲解
等腰直角三角形的三边之间有什么关系?
C
SA SB
SC
a
b
c
a b
a
b
c
c
等腰直角三角形斜边的平方等于两直角边的平方和.
其他的直角三角形也有这个性质吗?
A
B
C
新知讲解
每个小方格的面积均为1,请分别算出图中正方形A,B,C,A',B',C'的面积,看看能得出什么结论.
A
C
B
A'
C'
B'
新知讲解
A
C
B
正方形A的面积
正方形B的面积
正方形C的面积
9个小正方形的面积
9
4
4个小正方形的面积
新知讲解
A
C
B
正方形C的面积 4个直角三角形的面积 小正方形的面积
4 2 3
1
13
割
新知讲解
还有其他的方法吗?
A
C
B
正方形C的面积 大正方形的面积 4个直角三角形的面积
4 2 3
25
13
补
新知讲解
A
C
B
正方形A的面积
正方形B的面积
正方形C的面积
9
4
13
SA SB SC
新知讲解
正方形A'的面积
正方形B'的面积
正方形C'的面积
9
16
25
SA' SB' SC'
A'
C'
B'
新知讲解
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 两直角边的平方和等于斜边的平方.
由上面的几个例子,我们猜想:
a
b
c
新知讲解
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子,动手试一试,并证明刚刚的猜想.
a
b
c
a
b
a
b
c
图1
图2
新知讲解
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c .
勾股定理
勾
股
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
股
勾
弦
勾2 股2 弦2
a
b
c
归纳总结
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
例题分析
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得x=
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得x=
巩固练习
∴a=
(2)∵ b=15,∠A=30°
∴a=,c=
C
A
B
a
b
c
例2. 已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴AC×BC=AB×CD.
∴ CD=.
例题分析
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144=x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5
巩固练习
1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
易错提示
(宁波中考)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
C
链接中考
2.图中阴影部分是一个正方形,则此正方形的面积为__________.
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
8 cm
10 cm
36 cm
随堂检测
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
17
5
74或24
4.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
随堂检测
直角三角形的面积是(cm2).
5. 求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 = 172,
即x2=172-152=289–225=64
∴ x=±8 (负值舍去),
∴另一直角边长为8 cm,
随堂检测
6. 如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
解:∵AE=BE,
∴S△ABE=AE·BE=AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE=AB2=;
同理可得S△AHC+S△BCF=.
又∵AC2+BC2=AB2,
∴阴影部分的面积为AB2=.
随堂检测
勾股定理
内容
注意
课堂小结
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
