人教版九年级下册 28. 第3课时 特殊角的三角函数 课件(共24张PPT)
文档属性
| 名称 | 人教版九年级下册 28. 第3课时 特殊角的三角函数 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 13:12:12 | ||
图片预览







文档简介
(共24张PPT)
28.1 锐角三角函数
第3课时 特殊角的三角函数
第二十八章
1
课堂讲解
特殊角(30°,45°,60°)的三角函数值
特殊三角函数值的对应角
锐角三角函数间的关系
2
课时流程
逐点
导讲练
课堂小结
作业提升
为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;
②皮尺.请你设计一个测量方案,测出一棵大树
的高度.
1
知识点
特殊角(30°,45°,60°)的三角函数值
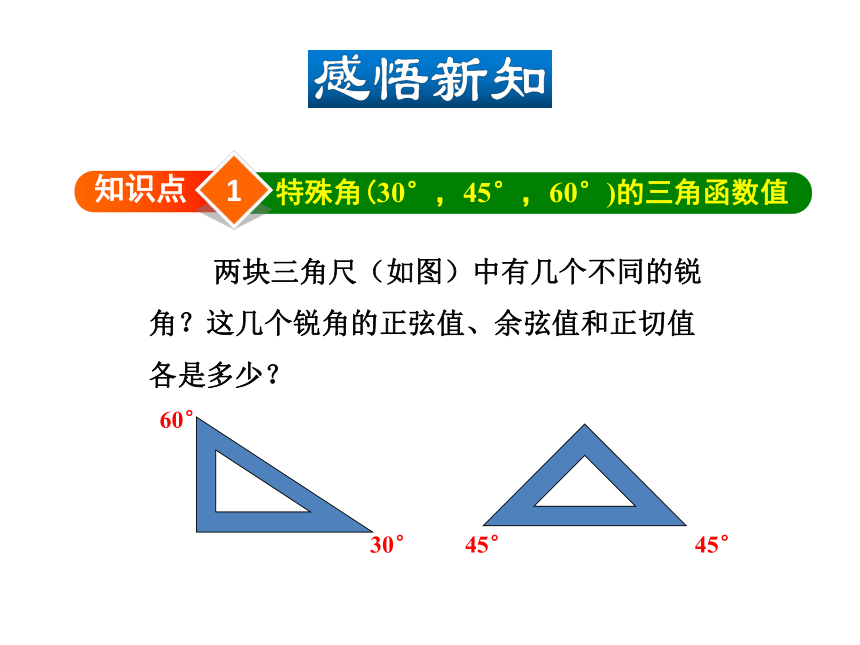
两块三角尺(如图)中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
30°
60°
45°
45°
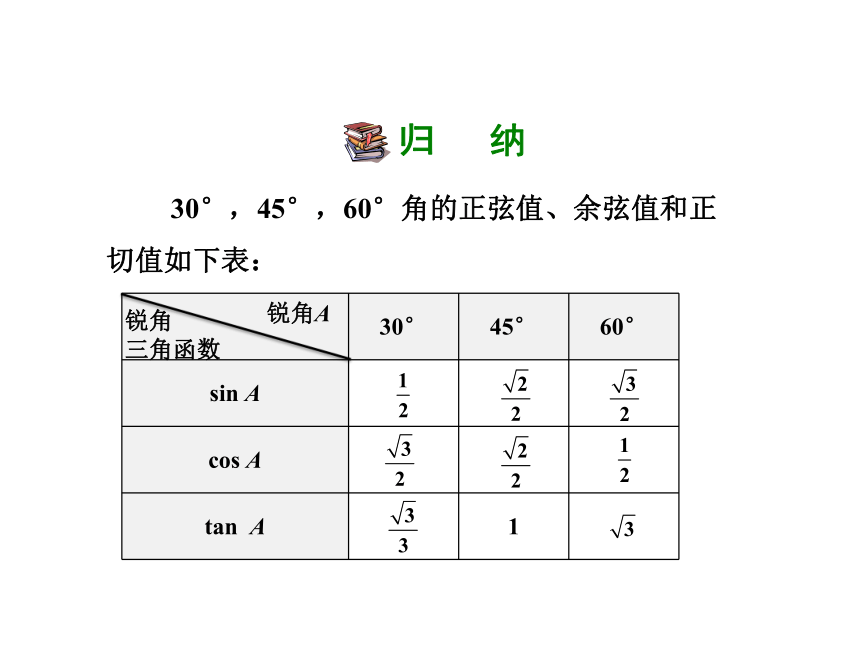
归 纳
30°,45°,60°角的正弦值、余弦值和正
切值如下表:
30° 45° 60°
sin A
cos A
tan A 1
锐角A
锐角
三角函数
例1 求下列各式的值:
(1)cos260°+sin260°;
(2)
解: (1) cos260°+sin260°
=1;
(2)
=0.
总 结
有关特殊角的三角函数值的计算,先直接写出
三角函数值,将运算转化为实数的混合运算,然后
根据实数的运算法则计算.
1 求下列各式的值:
(1)1-2sin 30°cos 30°;
(2)3tan 30°-tan 45°+ 2sin 60°;
(3)(cos230°+sin230°) ×tan 60°.
2 (2016·天津)sin60°的值等于( )
A. B. C. D.
(2015·滨州)下列运算:sin 30°= , =2 ,
π0=π,2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
2
知识点
特殊三角函数值的对应角
在Rt△ABC中,∠C=90°,BC= ,AC= ,求∠A、∠B的度数.
解: ∵tanA=
∴∠A=30°,∠B=60°.
.
归 纳
根据一个锐角的特殊的三角函数值,
也可以求出角的度数.
例2 (1)如图(1),在Rt△ABC中,∠C=90°,AB=
,BC= ,求∠A的度数.
(2)如图(2),AO是圆锥的高,OB是底面半径,
AO= OB,求 的度数.
B
A
O
A
B
C
(1)
(2)
解: (1)在图(1)中,
(2)在图(2)中,
总 结
由锐角和三角函数值之间的对应关系可得,给定一
个三角函数值,则必有一个锐角与之对应.由函数值求
特殊角.函数值的给出方式比较灵活,有直接给出的,
也有利用方程给出的,还有结合图形,需要计算后才能
得到的.不论以何种方式给出,解题的关键在于熟记角
和函数值之间的对应关系,灵活求解.有些题目要注意
锐角三角函数值的取值范围.
(2015·酒泉)已知α,β均为锐角,且满足
则α+β=________.
在△ABC中,∠A,∠B都是锐角,且sin A=
cos B= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3
知识点
锐角三角函数间的关系
(1)求特殊锐角的三角函数值的关键是先把它
转化为实数的运算,再根据实数的运算法
则计算.
(2)求锐角的度数的关键是先求其正弦值或余
弦值或正切值,然后对应特殊锐角的三角
函数值求角的度数.
.
(3)当A、B均为锐角时,若A≠B,则sinA≠sinB,
cosA≠cosB,tanA≠tanB.
(4)sin2α+cos2α=1,tanα=
.
例3 已知∠A为锐角,sin A= ,求∠A的其
他三角函数值.
.
导引:根据sin2 A+cos2 A=1,求出cos A的值,
然后根据tan A= ,求出tan A的值.
解:∵sin A= ,sin2 A+cos2 A=1,
∴ +cos2 A=1,
∴cos2 A=1-
∴cos A= (负值舍去).
.
∴
总 结
本题运用转化思想解题,即已知一个锐
角的三角函数值,可以根据平方关系:sin2 A
+cos2 A=1,商的关系:tan A= 求其
他三角函数值.
拓展:当∠A为锐角时,关系式sin2 A+
cos2 A=1可变形为:
在Rt△ABC中,∠C=90°,AC=40,AB=41.
(1)求sin A,cos A的值;
(2)求tan A·cos A的值.
在Rt△ABC中,∠C=90°,下列式子不一定
成立的是( )
A.tan A= B.sin2 A+cos2 A=1
C.sin2 A+sin2 B=1 D.tan A·tan B=1
(2015·汕尾)在Rt△ABC中,∠C=90°,
若sin A= ,则cos B的值是( )
A. B.
C. D.
30° 45° 60°
sin A
cos A
tan A 1
1.特殊角的三角函数值:
2.特殊角的三角函数值具有两重作用,由角
求值,由值同样也能求角.
3.从特殊角的三角函数值表上能观察到很多三
角函数的性质,如三个三角函数值的变化规律
(随角的变化,值的增减性)、正余弦关系(sinA=
cos(90°-∠A)),函数值的分界线等,平时注意
总结,以加深对三角函数的认识理解.
28.1 锐角三角函数
第3课时 特殊角的三角函数
第二十八章
1
课堂讲解
特殊角(30°,45°,60°)的三角函数值
特殊三角函数值的对应角
锐角三角函数间的关系
2
课时流程
逐点
导讲练
课堂小结
作业提升
为了测量一棵大树的高度,准备了如下测量工具:①含30°和60°两个锐角的三角尺;
②皮尺.请你设计一个测量方案,测出一棵大树
的高度.
1
知识点
特殊角(30°,45°,60°)的三角函数值
两块三角尺(如图)中有几个不同的锐角?这几个锐角的正弦值、余弦值和正切值各是多少?
30°
60°
45°
45°
归 纳
30°,45°,60°角的正弦值、余弦值和正
切值如下表:
30° 45° 60°
sin A
cos A
tan A 1
锐角A
锐角
三角函数
例1 求下列各式的值:
(1)cos260°+sin260°;
(2)
解: (1) cos260°+sin260°
=1;
(2)
=0.
总 结
有关特殊角的三角函数值的计算,先直接写出
三角函数值,将运算转化为实数的混合运算,然后
根据实数的运算法则计算.
1 求下列各式的值:
(1)1-2sin 30°cos 30°;
(2)3tan 30°-tan 45°+ 2sin 60°;
(3)(cos230°+sin230°) ×tan 60°.
2 (2016·天津)sin60°的值等于( )
A. B. C. D.
(2015·滨州)下列运算:sin 30°= , =2 ,
π0=π,2-2=-4,其中运算结果正确的个数为( )
A.4 B.3 C.2 D.1
2
知识点
特殊三角函数值的对应角
在Rt△ABC中,∠C=90°,BC= ,AC= ,求∠A、∠B的度数.
解: ∵tanA=
∴∠A=30°,∠B=60°.
.
归 纳
根据一个锐角的特殊的三角函数值,
也可以求出角的度数.
例2 (1)如图(1),在Rt△ABC中,∠C=90°,AB=
,BC= ,求∠A的度数.
(2)如图(2),AO是圆锥的高,OB是底面半径,
AO= OB,求 的度数.
B
A
O
A
B
C
(1)
(2)
解: (1)在图(1)中,
(2)在图(2)中,
总 结
由锐角和三角函数值之间的对应关系可得,给定一
个三角函数值,则必有一个锐角与之对应.由函数值求
特殊角.函数值的给出方式比较灵活,有直接给出的,
也有利用方程给出的,还有结合图形,需要计算后才能
得到的.不论以何种方式给出,解题的关键在于熟记角
和函数值之间的对应关系,灵活求解.有些题目要注意
锐角三角函数值的取值范围.
(2015·酒泉)已知α,β均为锐角,且满足
则α+β=________.
在△ABC中,∠A,∠B都是锐角,且sin A=
cos B= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3
知识点
锐角三角函数间的关系
(1)求特殊锐角的三角函数值的关键是先把它
转化为实数的运算,再根据实数的运算法
则计算.
(2)求锐角的度数的关键是先求其正弦值或余
弦值或正切值,然后对应特殊锐角的三角
函数值求角的度数.
.
(3)当A、B均为锐角时,若A≠B,则sinA≠sinB,
cosA≠cosB,tanA≠tanB.
(4)sin2α+cos2α=1,tanα=
.
例3 已知∠A为锐角,sin A= ,求∠A的其
他三角函数值.
.
导引:根据sin2 A+cos2 A=1,求出cos A的值,
然后根据tan A= ,求出tan A的值.
解:∵sin A= ,sin2 A+cos2 A=1,
∴ +cos2 A=1,
∴cos2 A=1-
∴cos A= (负值舍去).
.
∴
总 结
本题运用转化思想解题,即已知一个锐
角的三角函数值,可以根据平方关系:sin2 A
+cos2 A=1,商的关系:tan A= 求其
他三角函数值.
拓展:当∠A为锐角时,关系式sin2 A+
cos2 A=1可变形为:
在Rt△ABC中,∠C=90°,AC=40,AB=41.
(1)求sin A,cos A的值;
(2)求tan A·cos A的值.
在Rt△ABC中,∠C=90°,下列式子不一定
成立的是( )
A.tan A= B.sin2 A+cos2 A=1
C.sin2 A+sin2 B=1 D.tan A·tan B=1
(2015·汕尾)在Rt△ABC中,∠C=90°,
若sin A= ,则cos B的值是( )
A. B.
C. D.
30° 45° 60°
sin A
cos A
tan A 1
1.特殊角的三角函数值:
2.特殊角的三角函数值具有两重作用,由角
求值,由值同样也能求角.
3.从特殊角的三角函数值表上能观察到很多三
角函数的性质,如三个三角函数值的变化规律
(随角的变化,值的增减性)、正余弦关系(sinA=
cos(90°-∠A)),函数值的分界线等,平时注意
总结,以加深对三角函数的认识理解.
