北师大版数学七年级下册 6.3 等可能事件的概率 第3课时 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 6.3 等可能事件的概率 第3课时 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 654.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 16:50:04 | ||
图片预览





文档简介
(共16张PPT)
第六章 概率初步
3 等可能事件的概率(第3课时)
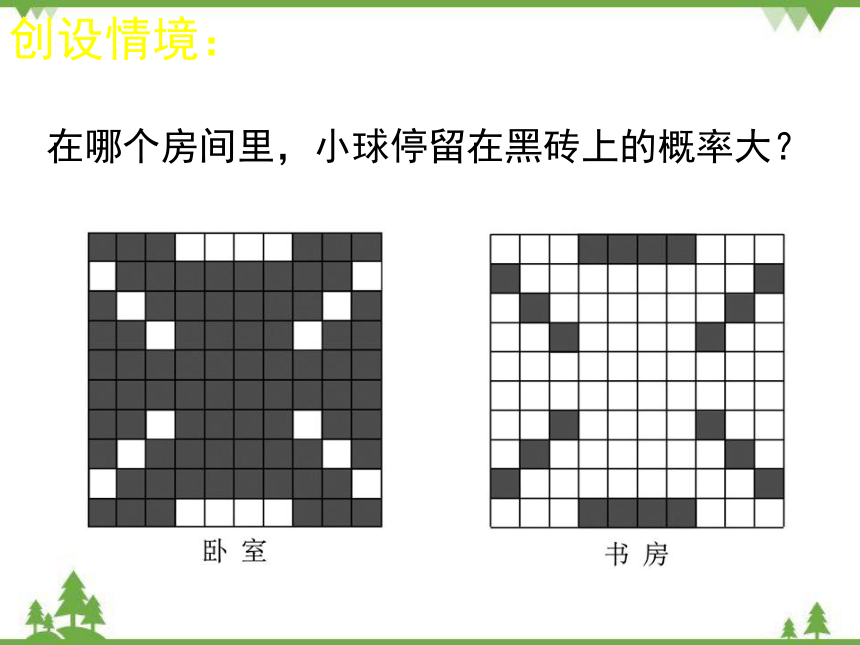
创设情境:
在哪个房间里,小球停留在黑砖上的概率大?
如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
5个方砖的面积
20个方砖的面积
P(小球最终停在黑砖上)=
4
1
=
迷茫的小白兔
1. 题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么? 2.小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能出现的结果有几种? 3.小球停留在黑砖上的概率是多少?怎样计算? 4.小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系? 5.如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖上的概率是多少?
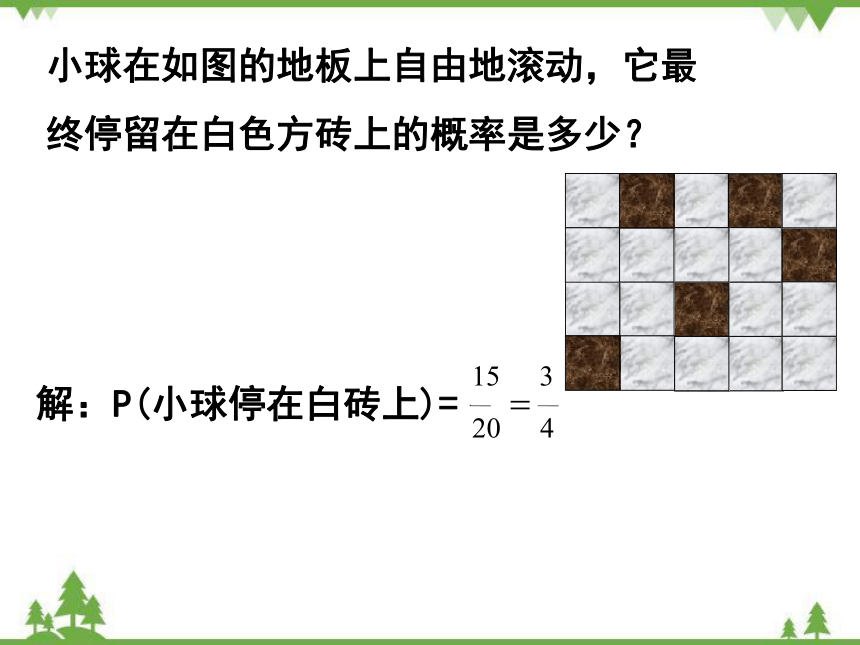
小球在如图的地板上自由地滚动,它最
终停留在白色方砖上的概率是多少?
解:P(小球停在白砖上)=
4
3
=
20
15
挑战自我 激情无限
如图,是自由转动的转盘,被均匀分成10部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
1
2
3
4
5
6
7
8
9
10
“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)= 。
易错题
例1 某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,
他获得的购物券的概率
是多少?他得到100元、
50元、20元的购物券的
概率分别是多少?
转盘被等分成20个扇形,其中1个是红色,2个是黄色,4个是绿色,对甲顾客来说:
分 析:
解:
P(获得购物券)=
P(获得100元购物券)=
P(获得50元购物券)=
P(获得20元购物券)=
1+2+4
20
20
1
10
1
5
1
20
7
=
利用自己手中的转盘,转盘被等分成16个扇形,请借助身边的工具,设计一个游戏,使得自由转动这个转盘,当它停止转动时,指针落在红色区域的概率为3/8。
超级制作秀
只要红色区域占6份即可。
成果展示秀
。
A. 事件
区域面积
概率
面积比
至胜秘笈
该事件所占区域的面积
事件的概率 =
总面积
B. 公式总结:
第六章 概率初步
3 等可能事件的概率(第3课时)
创设情境:
在哪个房间里,小球停留在黑砖上的概率大?
如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,它最终停留在黑砖上的概率是多少?
5个方砖的面积
20个方砖的面积
P(小球最终停在黑砖上)=
4
1
=
迷茫的小白兔
1. 题中所说“自由地滚动,并随机停留在某块方砖上”说明了什么? 2.小球停留在方砖上所有可能出现的结果有几种?停留在黑砖上可能出现的结果有几种? 3.小球停留在黑砖上的概率是多少?怎样计算? 4.小球停留在白砖上的概率是多少?它与停留在黑砖上的概率有何关系? 5.如果黑砖的面积是5平方米,整个地板的面积是20平方米,小球停留在黑砖上的概率是多少?
小球在如图的地板上自由地滚动,它最
终停留在白色方砖上的概率是多少?
解:P(小球停在白砖上)=
4
3
=
20
15
挑战自我 激情无限
如图,是自由转动的转盘,被均匀分成10部分,随机转动,则
1.P(指针指向6)= ;
2.P(指针指向奇数)= ;
3.P(指针指向3的倍数)= ;
4.P(指针指向15)= ;
5.P(指针指向的数大于4)= ;
6.P(指针指向的数小于11)= .
1
2
3
4
5
6
7
8
9
10
“十运会”射箭比赛休息之余,一名工作人员发现这样的一幕 :有一只蜘蛛在箭靶上爬来爬去,最终停下来,已知两圆的半径分别是1cm和2cm,则P(蜘蛛停留在黄色区域内)= 。
易错题
例1 某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会。如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以获得100元、50元,20元的购物券。(转盘被等分成20个扇形)
甲顾客购物120元,
他获得的购物券的概率
是多少?他得到100元、
50元、20元的购物券的
概率分别是多少?
转盘被等分成20个扇形,其中1个是红色,2个是黄色,4个是绿色,对甲顾客来说:
分 析:
解:
P(获得购物券)=
P(获得100元购物券)=
P(获得50元购物券)=
P(获得20元购物券)=
1+2+4
20
20
1
10
1
5
1
20
7
=
利用自己手中的转盘,转盘被等分成16个扇形,请借助身边的工具,设计一个游戏,使得自由转动这个转盘,当它停止转动时,指针落在红色区域的概率为3/8。
超级制作秀
只要红色区域占6份即可。
成果展示秀
。
A. 事件
区域面积
概率
面积比
至胜秘笈
该事件所占区域的面积
事件的概率 =
总面积
B. 公式总结:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
