北师大版八年级数学下册5.4.2分式方程的解法 课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册5.4.2分式方程的解法 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 17:07:43 | ||
图片预览


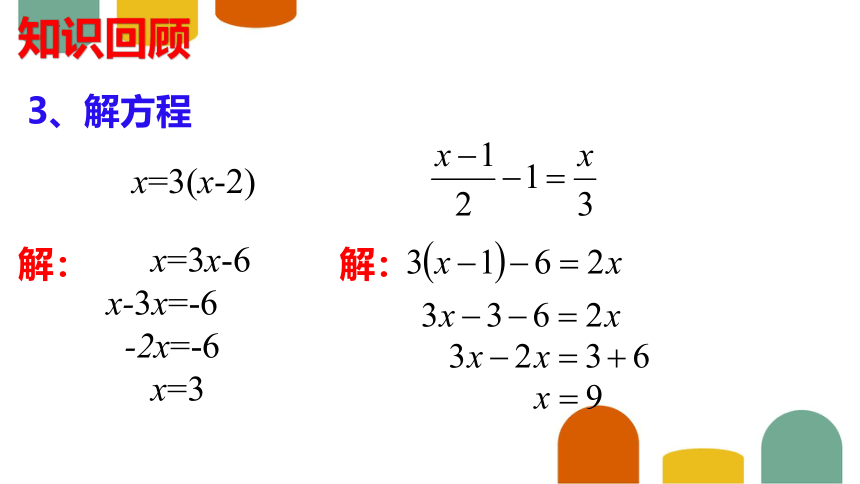




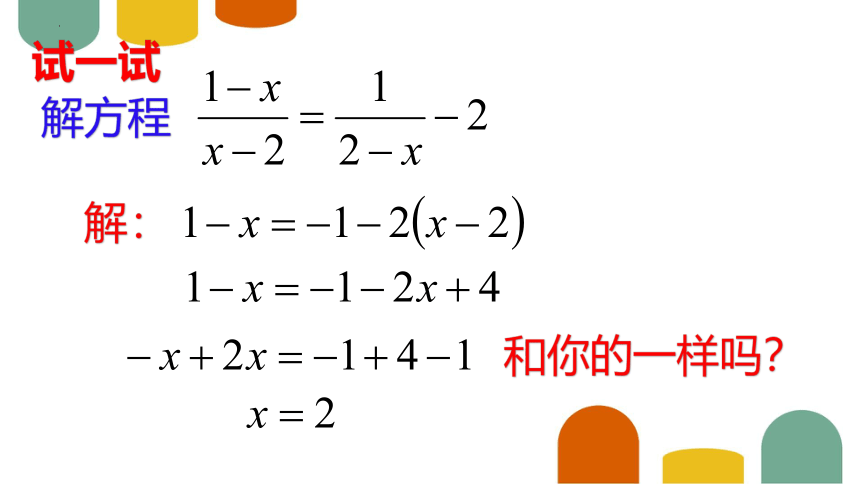
文档简介
(共21张PPT)
5.4.2分式方程的解法
梦想,只有坚持才能实现。要学会把努力当成一种习惯,而不是三分钟热度。每一个你羡慕的收获,背后都是无尽的汗水与付出!
知识回顾
1、什么是分式方程?
分母中含有未知数的方程叫做分式方程.
2、解一元一次方程的一般步骤有哪些?
①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
知识回顾
3、解方程
x=3(x-2)
解:
x=3x-6
x-3x=-6
-2x=-6
x=3
解:
课本引例
还记得什么是方程的解吗?
你能设法求出上一节课列出的分式方程的解吗?
使方程左右两边相等的未知数的值
学生可能有多种解法,尽可能发挥孩子的潜力。
解法1:
解法2:
解法3:
解法4:
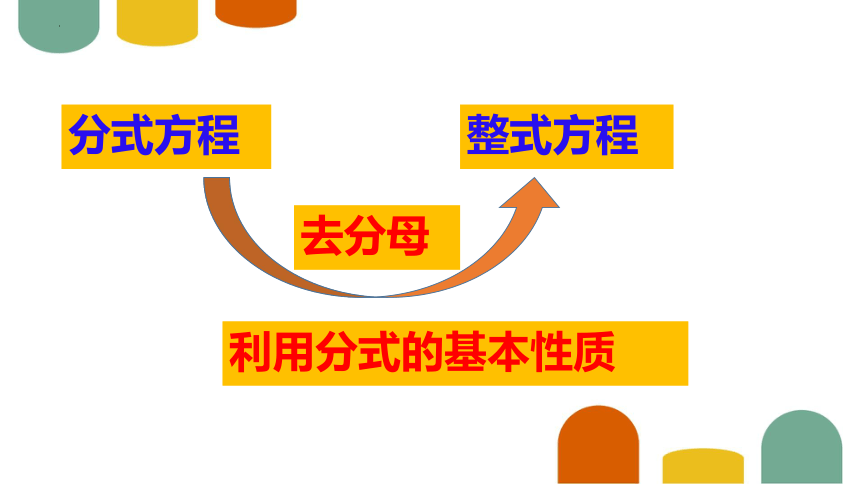
分式方程
整式方程
去分母
利用分式的基本性质
例1
解方程
将x=3代人原方程,得:
左边=1,右边=1,左边=右边.
所以,x=3是原方程的根.
解:方程两边都乘x(x-2),得
x=3(x-2).
解这个方程,得x=3.
检验:
想一想
一定要检验未知数的值是方程的解吗?
试一试
解方程
解:
和你的一样吗?
议一议
解方程
你认为x=2是原方程的解吗?
在这里,x=2不是原方程的根,因为它使得原分式方程的分母为零,我们称它为原方程的增根.
产生增根的原因是,我们在方程的两边同乘了一个使分母为零的整式。
因为解分式方程可能产生增根,所以解分式方程必须检验.
通常只需检验所得的根是否使原方程中分式的分母的值等于零就可以了.
进一步理解分式方程的增根.
事实上,对于分式方程,当分式中分母的值为零时,相应的分式没有意义。所以,分式方程不允许未知数取那些使分母的值为零的值,即分式方程本身就隐含着分母不为零的条件.当把分式方程转化为整式方程以后,这种限制取消了。换言之,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好是原方程未知数的允许值之外的值,那么就会出现增根.因为解分式方程可能出现增根,所以解分式方程时,验根是必要的步骤。验根的方法有两种,一种方法是把求得的的未知数的值代入原方程进行检验,这种方法追单,而且可以检查解方程时有无计算草错误;另一种方法是把求得的未知数的值代人的分母,看分母的值是否等于零,这种方法不能检查解方程过程中出现的其他错误。
例2
解方程
经检验,x=4是原方程的根.
解:方程两边都乘2x,得
960-600=90x
解这个方程,得x=4.
想一想
解分式方程一般需要经过哪几个步骤?
④检验由这个整式方程所得的根是不是原方程的根,从而判定方程根的情况.
①找各分式的最简公分母
②原方程两边都乘各分式的最简公分母,转化为整式方程;
③解这个整式方程;
练一练
解下列分式方程
分式方程
整式方程
去分母
利用分式的基本性质
解方程
检验
代入原方程检验
当堂检测
1.解下列分式方程
当堂检测
2.解下列分式方程
当堂检测
3.小明解方程过程如下:他的解法对吗?为什么?
当堂检测
4.某市为治理污水,需要铺设一段全长为3000 m的污水排放管道。为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加 25%,结果提前30天完成这一任务.实际每天铺设多长管道
当堂检测
5.某质检部门抽取甲、乙两厂相同数量的产品进行质量检测,结果甲厂有48 件合格产品,乙厂有 45 件合格产品,甲厂产品的合格率比乙厂高5%,求甲厂产品的合格率。
5.4.2分式方程的解法
梦想,只有坚持才能实现。要学会把努力当成一种习惯,而不是三分钟热度。每一个你羡慕的收获,背后都是无尽的汗水与付出!
知识回顾
1、什么是分式方程?
分母中含有未知数的方程叫做分式方程.
2、解一元一次方程的一般步骤有哪些?
①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
知识回顾
3、解方程
x=3(x-2)
解:
x=3x-6
x-3x=-6
-2x=-6
x=3
解:
课本引例
还记得什么是方程的解吗?
你能设法求出上一节课列出的分式方程的解吗?
使方程左右两边相等的未知数的值
学生可能有多种解法,尽可能发挥孩子的潜力。
解法1:
解法2:
解法3:
解法4:
分式方程
整式方程
去分母
利用分式的基本性质
例1
解方程
将x=3代人原方程,得:
左边=1,右边=1,左边=右边.
所以,x=3是原方程的根.
解:方程两边都乘x(x-2),得
x=3(x-2).
解这个方程,得x=3.
检验:
想一想
一定要检验未知数的值是方程的解吗?
试一试
解方程
解:
和你的一样吗?
议一议
解方程
你认为x=2是原方程的解吗?
在这里,x=2不是原方程的根,因为它使得原分式方程的分母为零,我们称它为原方程的增根.
产生增根的原因是,我们在方程的两边同乘了一个使分母为零的整式。
因为解分式方程可能产生增根,所以解分式方程必须检验.
通常只需检验所得的根是否使原方程中分式的分母的值等于零就可以了.
进一步理解分式方程的增根.
事实上,对于分式方程,当分式中分母的值为零时,相应的分式没有意义。所以,分式方程不允许未知数取那些使分母的值为零的值,即分式方程本身就隐含着分母不为零的条件.当把分式方程转化为整式方程以后,这种限制取消了。换言之,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好是原方程未知数的允许值之外的值,那么就会出现增根.因为解分式方程可能出现增根,所以解分式方程时,验根是必要的步骤。验根的方法有两种,一种方法是把求得的的未知数的值代入原方程进行检验,这种方法追单,而且可以检查解方程时有无计算草错误;另一种方法是把求得的未知数的值代人的分母,看分母的值是否等于零,这种方法不能检查解方程过程中出现的其他错误。
例2
解方程
经检验,x=4是原方程的根.
解:方程两边都乘2x,得
960-600=90x
解这个方程,得x=4.
想一想
解分式方程一般需要经过哪几个步骤?
④检验由这个整式方程所得的根是不是原方程的根,从而判定方程根的情况.
①找各分式的最简公分母
②原方程两边都乘各分式的最简公分母,转化为整式方程;
③解这个整式方程;
练一练
解下列分式方程
分式方程
整式方程
去分母
利用分式的基本性质
解方程
检验
代入原方程检验
当堂检测
1.解下列分式方程
当堂检测
2.解下列分式方程
当堂检测
3.小明解方程过程如下:他的解法对吗?为什么?
当堂检测
4.某市为治理污水,需要铺设一段全长为3000 m的污水排放管道。为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加 25%,结果提前30天完成这一任务.实际每天铺设多长管道
当堂检测
5.某质检部门抽取甲、乙两厂相同数量的产品进行质量检测,结果甲厂有48 件合格产品,乙厂有 45 件合格产品,甲厂产品的合格率比乙厂高5%,求甲厂产品的合格率。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
