人教版七年级数学下册 8.3 实际问题与二元一次方程组 课件(共40张)
文档属性
| 名称 | 人教版七年级数学下册 8.3 实际问题与二元一次方程组 课件(共40张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 665.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
人教版七年级数学下册
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
解:(1) ②×2,得2x+4y=-4.③
(1)
2x-3y=3,
x+2y=2.
①
②
③-①,得7y=-7,
解得y=-1.
将y=-1代入②,得x=0.
∴这个方程组的解是
x=0,
y=-1.
一、复习巩固
解下列方程组:
(2)
解:(2)整理,得
由①×5,得25x-5y=180.③
由②+③,得26x=208,即x=8.
把x=8代入①,得y=4.
∴原方程组的解为
(2)
5x-y=36,①
x+5y=28.②
x=8
y=4
二、探究新知
探究1养牛场原有 30 头大牛和 15 头小牛,1 天约用饲料 675 kg;一周后又购进 12 头大牛和 5 头小牛,这时 1 天约用饲料 940 kg.饲养员李大叔估计每只大牛 1 天约需饲料 18~20 kg,每只小牛 1 天约需饲料 7 ~8 kg. 你能否通过计算检验他的估计吗?(教材P99)
探究1
探究 养牛场原有30头大牛和15头小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg.饲养员李大叔估计平均每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7 ~8 kg.你能否通过计算检验他的估计?
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中哪些是已知量,哪些是未知量?有几个等量关系?
分析:设平均每只大牛和每只小牛1天各约需饲料x千克和y千克 ,根据两种情况的饲料用量,利用相等关系,列方程组
解这个方程组得
这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg。因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
你答对了吗?
解得:
20
5
化简得:
①
②
解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg。
依题意得
⑴审题,弄清 ,及题中的 ;
⑵设未知数,可 ,也可 ;
⑶根据题目中所给出的 ,列出方程组;
⑷ ,
(5)检验解的正确性;
(6)答:书写完整
题意
直接设元
间接设元
等量关系
解方程组
等量关系
列方程组解应用题的一般步骤:
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,
针对练习
答:小明估计不准确。2米的应取8段,1米的 应取2段。
解得:
依题意得
探究1
探究 养牛场原有30头大牛和15头小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg.饲养员李大叔估计平均每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7 ~8 kg.你能否通过计算检验他的估计?
这就是说,平均每头母牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对母牛的食量估计较准确,对小牛的食量估计偏高。
饲养员李大叔的估计正确吗?
探究2
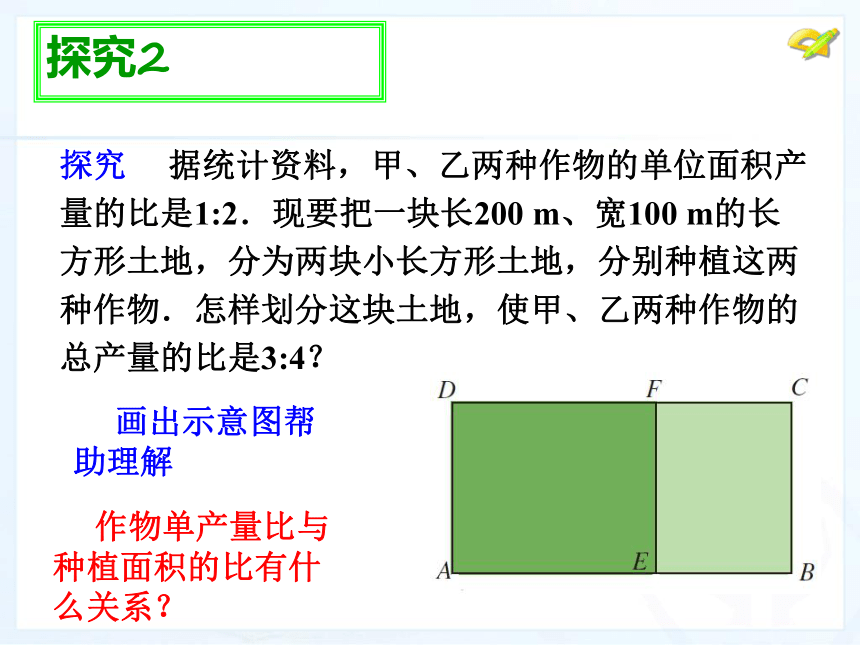
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
画出示意图帮助理解
作物单产量比与种植面积的比有什么关系?
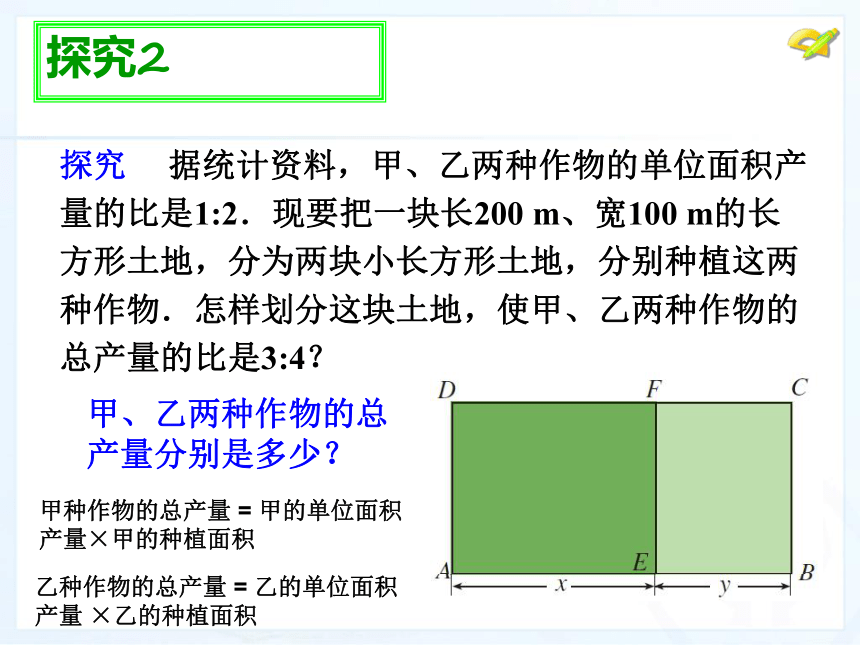
甲、乙两种作物的总产量分别是多少?
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究2
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新知二 列二元一次方程组解答几何问题
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
合作探究
这里研究的实际上是什么问题?
把一个长方形分成两个小长方形有哪些分割方式?
方法1
竖着画,把长分成两段,则宽不变
方法2
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
动手试着画一画
目标:甲、乙两种作物的总产量的比是3:4
问题分析
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
方法1
列方程组:
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究2
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:100y×2=3:4.
x
y
200m
100m
x+y=200,
解得
x=120,
y=80.
你觉得该如何答题比较完整呢?
甲种作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
方法1
解法一
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100,
乙种作物
甲种作物
解:过点E作EF⊥BC,交BC于点F. 设DE=xm,AE=ym.
200x:400y=3:4.
200y
200x
x=60,
y=40.
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
方法2
解法二
① 能列二元一次方程组解决的实际问题,一般都可以通过列一元一次方程加以解决.但是,随着实际问题中未知量的增多和数量关系的复杂,列方程组将更加简单直接,因为问题有几个相等关系就可以列出几个方程.
② 两者相同点是都需要先分析题意,把实际问题转化为数学问题(设未知数,列方程或方程组),再检验解的合理性,进而得到实际问题的解,这一过程就是建模的过程.
列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
1.如图,宽为 50 cm 的长方形图案由 10 个相同的小长方形拼成,则每个小长方形的长和宽分别是多少?
解:设每个小长方形的宽为 x cm,
长为 y cm.观察图形,得
把①代入②,得 x+4x = 50.解得 x = 10.
把 x = 10 代入①,得 y = 40.
∴这个方程组的解为
答:每个小长方形的长为 40 cm,宽为 10 cm.
练
习
2.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,
由题意得:
X-4
4
y
2
Ⅰ
Ⅱ
如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
探究3
公路20 km
长青化工厂
公路10 km
铁路110 km
铁路120 km
B
A
探究3 如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
你知道吗
解:设产品重x吨,原料重y吨。填表:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
加工有损耗
探究3 如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解方程组得:
答:多1887800元。
列方程组:
售价-成本=利润
问题 你发现其它等量关系了吗?如何列出方程组并求解?
所以原方程组的解为
先化简,得
②
①
由① 得
代入③ ,得
③
把③代入② ,得
解得
解:设产品重x吨,原料重y吨
这个实际问题的答案是什么?
销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2 400 000-400 000-112 200=1 887 800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
检验作答
解方程组:
代入法;
加减法.
几何问题
三、归纳新知
有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨.求3辆大车与5辆小车一次可以运货多少吨?
练
习
课本102页复习巩固第5题
解:设大车一次可以运货x吨,小车一次可以运货y吨.由题意,得
②-①×2,得x=4.
把x=4代入①,得4×2+3y=15.5.解得y=2.5.
∴3x+5y=3×4+5×2.5=24.5.
答:3辆大车与5辆小车一次可以运货24.5吨.
列二元一次方程组解应用题的一般步骤:
(1)审题,弄清题中的数量关系
(2)设两个未知数,并用含未知数的式子表示各自相关的量
(3)根据题中的等量关系列方程组
(4)解方程组,求出未知数的值
(5)检验解的正确性和合理性,写出答案
四、课堂小结
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
1.现用 190 张铁皮做盒子,每张铁皮可制 8 个盒身或 22 个盒底,而一个盒身与两个盒底配成一个盒子.设用 x 张铁皮做盒身,y 张铁皮做盒底,则可列方程组为( )
A
A
x+y=190
2×8x=22y
C
2y+x=190
8x=22y
B
x+y=190
2×22y=8x
D
2y+x=190
2×8x=22y
五、拓展训练
2. A 地至 B 地的航线长 9750 km,一架飞机从A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为x km/h,风速为y km/h.
由题意,得 化简,得
①+②,得2x=1530. 解得x=765.
把x=765代入①, 得y=15.
∴这个方程组的解为
课本101页复习巩固第2题
3.一支部队第一天行军 4 h,第二天行军 5 h,两天共行军 98 km,且第一天比第二天少走 2 km,第一天和第二天行军的平均速度各是多少?
解:设第一天行军的平均速度为 x km/h,第二天行军的平均速度为 y km/h.
由题意,得
解得
答:第一天行军的平均速度为 12 km/h,第二天行军的平均速度为 10 km/h.
课本101页复习巩固第3题
6.从甲地到乙地的路有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分,从乙地到甲地需42分.甲地到乙地全程是多少?
课本102页复习巩固第6题
7.用含药 30% 和 75% 的两种防腐药水,配制含药 50% 的防腐药水 18 kg,两种药水各需多少千克?
解:设需含药 30% 的药水 x kg,含药 75% 的药水 y kg
∴这个方程组的解为
答:两种药水各需 10 kg,8 kg.
课本102页复习巩固第7题
9.某家商店的帐目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
课本102页复习巩固第9题
解:有误,理由:设一支牙刷的价格为x元,一盒牙膏的价格为y元.由题意,得
即:
方程组无解.
∴这个记录有误.
7.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
人教版七年级数学下册
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
解:(1) ②×2,得2x+4y=-4.③
(1)
2x-3y=3,
x+2y=2.
①
②
③-①,得7y=-7,
解得y=-1.
将y=-1代入②,得x=0.
∴这个方程组的解是
x=0,
y=-1.
一、复习巩固
解下列方程组:
(2)
解:(2)整理,得
由①×5,得25x-5y=180.③
由②+③,得26x=208,即x=8.
把x=8代入①,得y=4.
∴原方程组的解为
(2)
5x-y=36,①
x+5y=28.②
x=8
y=4
二、探究新知
探究1养牛场原有 30 头大牛和 15 头小牛,1 天约用饲料 675 kg;一周后又购进 12 头大牛和 5 头小牛,这时 1 天约用饲料 940 kg.饲养员李大叔估计每只大牛 1 天约需饲料 18~20 kg,每只小牛 1 天约需饲料 7 ~8 kg. 你能否通过计算检验他的估计吗?(教材P99)
探究1
探究 养牛场原有30头大牛和15头小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg.饲养员李大叔估计平均每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7 ~8 kg.你能否通过计算检验他的估计?
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中哪些是已知量,哪些是未知量?有几个等量关系?
分析:设平均每只大牛和每只小牛1天各约需饲料x千克和y千克 ,根据两种情况的饲料用量,利用相等关系,列方程组
解这个方程组得
这就是说,每只大牛约需饲料20kg,每只小牛约需饲料5kg。因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
你答对了吗?
解得:
20
5
化简得:
①
②
解:设平均每只大牛和每只小牛1天各约需饲料xkg和ykg。
依题意得
⑴审题,弄清 ,及题中的 ;
⑵设未知数,可 ,也可 ;
⑶根据题目中所给出的 ,列出方程组;
⑷ ,
(5)检验解的正确性;
(6)答:书写完整
题意
直接设元
间接设元
等量关系
解方程组
等量关系
列方程组解应用题的一般步骤:
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
解:设应取2米的x段,1米的y段,
针对练习
答:小明估计不准确。2米的应取8段,1米的 应取2段。
解得:
依题意得
探究1
探究 养牛场原有30头大牛和15头小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg.饲养员李大叔估计平均每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7 ~8 kg.你能否通过计算检验他的估计?
这就是说,平均每头母牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对母牛的食量估计较准确,对小牛的食量估计偏高。
饲养员李大叔的估计正确吗?
探究2
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
画出示意图帮助理解
作物单产量比与种植面积的比有什么关系?
甲、乙两种作物的总产量分别是多少?
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究2
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
据统计资料,甲、乙两种作物的单位面积产量的比1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新知二 列二元一次方程组解答几何问题
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
A
D
C
B
合作探究
这里研究的实际上是什么问题?
把一个长方形分成两个小长方形有哪些分割方式?
方法1
竖着画,把长分成两段,则宽不变
方法2
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
动手试着画一画
目标:甲、乙两种作物的总产量的比是3:4
问题分析
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
方法1
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
方法1
列方程组:
探究 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
探究2
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:100y×2=3:4.
x
y
200m
100m
x+y=200,
解得
x=120,
y=80.
你觉得该如何答题比较完整呢?
甲种作物
乙种
作物
解:
过点E作EF⊥AB,交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
方法1
解法一
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100,
乙种作物
甲种作物
解:过点E作EF⊥BC,交BC于点F. 设DE=xm,AE=ym.
200x:400y=3:4.
200y
200x
x=60,
y=40.
解得
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
方法2
解法二
① 能列二元一次方程组解决的实际问题,一般都可以通过列一元一次方程加以解决.但是,随着实际问题中未知量的增多和数量关系的复杂,列方程组将更加简单直接,因为问题有几个相等关系就可以列出几个方程.
② 两者相同点是都需要先分析题意,把实际问题转化为数学问题(设未知数,列方程或方程组),再检验解的合理性,进而得到实际问题的解,这一过程就是建模的过程.
列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
1.如图,宽为 50 cm 的长方形图案由 10 个相同的小长方形拼成,则每个小长方形的长和宽分别是多少?
解:设每个小长方形的宽为 x cm,
长为 y cm.观察图形,得
把①代入②,得 x+4x = 50.解得 x = 10.
把 x = 10 代入①,得 y = 40.
∴这个方程组的解为
答:每个小长方形的长为 40 cm,宽为 10 cm.
练
习
2.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
解:设长方形的长为xcm,宽为ycm,
由题意得:
X-4
4
y
2
Ⅰ
Ⅱ
如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
探究3
公路20 km
长青化工厂
公路10 km
铁路110 km
铁路120 km
B
A
探究3 如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
你知道吗
解:设产品重x吨,原料重y吨。填表:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
加工有损耗
探究3 如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
解方程组得:
答:多1887800元。
列方程组:
售价-成本=利润
问题 你发现其它等量关系了吗?如何列出方程组并求解?
所以原方程组的解为
先化简,得
②
①
由① 得
代入③ ,得
③
把③代入② ,得
解得
解:设产品重x吨,原料重y吨
这个实际问题的答案是什么?
销售款:8 000×300=2 400 000元;
原料费:1 000×400=400 000元;
运输费:15 000+97 200=112 200元.
2 400 000-400 000-112 200=1 887 800元.
这批产品的销售款比原料费与运输费的和多1 887 800元.
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据2个等量关系列出方程组
检验作答
解方程组:
代入法;
加减法.
几何问题
三、归纳新知
有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨,5辆大车与6辆小车一次可以运货35吨.求3辆大车与5辆小车一次可以运货多少吨?
练
习
课本102页复习巩固第5题
解:设大车一次可以运货x吨,小车一次可以运货y吨.由题意,得
②-①×2,得x=4.
把x=4代入①,得4×2+3y=15.5.解得y=2.5.
∴3x+5y=3×4+5×2.5=24.5.
答:3辆大车与5辆小车一次可以运货24.5吨.
列二元一次方程组解应用题的一般步骤:
(1)审题,弄清题中的数量关系
(2)设两个未知数,并用含未知数的式子表示各自相关的量
(3)根据题中的等量关系列方程组
(4)解方程组,求出未知数的值
(5)检验解的正确性和合理性,写出答案
四、课堂小结
实际问题
数学问题
(二元一次方程组)
解方程组
数学问题的解
(二元一次方程组的解)
双检验
实际问题
的答案
代入法
加减法
(消元)
设未知数、列方程组
利用二元一次方程组分析和解决实际问题的基本过程:
1.现用 190 张铁皮做盒子,每张铁皮可制 8 个盒身或 22 个盒底,而一个盒身与两个盒底配成一个盒子.设用 x 张铁皮做盒身,y 张铁皮做盒底,则可列方程组为( )
A
A
x+y=190
2×8x=22y
C
2y+x=190
8x=22y
B
x+y=190
2×22y=8x
D
2y+x=190
2×8x=22y
五、拓展训练
2. A 地至 B 地的航线长 9750 km,一架飞机从A 地顺风飞往 B 地需 12.5 h,它逆风飞行同样的航线需 13 h,求飞机的平均速度与风速.
解:设飞机的平均速度为x km/h,风速为y km/h.
由题意,得 化简,得
①+②,得2x=1530. 解得x=765.
把x=765代入①, 得y=15.
∴这个方程组的解为
课本101页复习巩固第2题
3.一支部队第一天行军 4 h,第二天行军 5 h,两天共行军 98 km,且第一天比第二天少走 2 km,第一天和第二天行军的平均速度各是多少?
解:设第一天行军的平均速度为 x km/h,第二天行军的平均速度为 y km/h.
由题意,得
解得
答:第一天行军的平均速度为 12 km/h,第二天行军的平均速度为 10 km/h.
课本101页复习巩固第3题
6.从甲地到乙地的路有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分,从乙地到甲地需42分.甲地到乙地全程是多少?
课本102页复习巩固第6题
7.用含药 30% 和 75% 的两种防腐药水,配制含药 50% 的防腐药水 18 kg,两种药水各需多少千克?
解:设需含药 30% 的药水 x kg,含药 75% 的药水 y kg
∴这个方程组的解为
答:两种药水各需 10 kg,8 kg.
课本102页复习巩固第7题
9.某家商店的帐目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
课本102页复习巩固第9题
解:有误,理由:设一支牙刷的价格为x元,一盒牙膏的价格为y元.由题意,得
即:
方程组无解.
∴这个记录有误.
7.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
