8-3实际问题与二元一次方程组课件——人教版七年级下册数学(20张ppt)
文档属性
| 名称 | 8-3实际问题与二元一次方程组课件——人教版七年级下册数学(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 17:23:14 | ||
图片预览








文档简介
(共20张PPT)
8.3 实际问题与二元一次方程组
学习目标:
能分析实际问题中的数量关系,会设未知数,列方程组并求解,得到实际问题的答案,体会数学建模思想。
学习重点:
探究“二元一次方程组解决实际问题”。
探究1 养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg。饲养员李大叔估计平均每只大牛1天约需饲料18~20 kg,每只小牛1天约需饲料7 ~8 kg。 你能否通过计算检验他的估计?
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中哪些是已知量,哪些是未知量?有几个等量关系?
问题3 如何解决这一问题?
解:设每头大牛和每头小牛1天分别约用饲料x kg、y kg,根据题意,得
列一元一次方程能解决这个问题吗?
请你解这个方程组,并交流一下你是如何解这个方程组的?
①
②
解:①×4-②×3,得
代入①,得
所以,方程组的解是
(1)在列方程组之前我们先做了哪些工作?
(2)列方程组解决实际问题的一般步骤是什么?
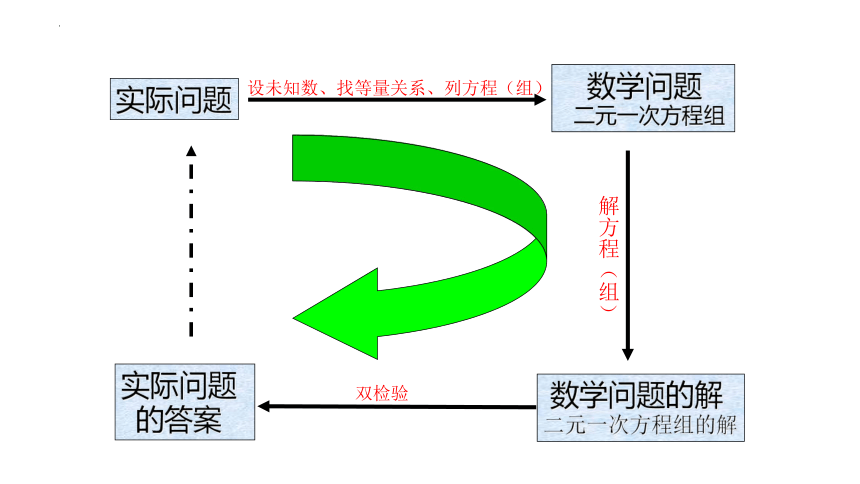
实际问题
设未知数、找等量关系、列方程(组)
数学问题
二元一次方程组
解方程(组)
数学问题的解
二元一次方程组的解
双检验
实际问题
的答案
你认为列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
① 能列二元一次方程组解决的实际问题,一般都可以通过列一元一次方程加以解决。但是,随着实际问题中未知量的增多和数量关系的复杂,列方程组将更加简单直接,因为问题有几个相等关系就可以列出几个方程。
② 两者相同点是都需要先分析题意,把实际问题转化为数学问题(设未知数,列方程或方程组),再检验解的合理性,进而得到实际问题的解,这一过程就是建模的过程。
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
100
200
设什么为未知数
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
x
y
E
F
列方程
x+y=200
甲总产量:乙总产量=3:4
总产量与什么有关
甲
100x
乙
200y
100x:200y=3:4
解:作EF⊥CB,交CB,AD于点F,E.设BF为x m,FC为y m.
200
100
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
x
y
E
F
甲
100x
乙
200y
解:作EF⊥CB,交CB,AD于点F,E.设BF为xm,FC为ym.
200
100
解得:
回顾交流
1、列方程组解应用题的步骤是什么?
审:审题,分析题中已知什么,求什么,明确各数量之间的关系
(找:找出能够表示应用题全部意义的两个相等关系)
设:设未知数(一般求什么,就设什么为x、y,注意单位)
列:根据这两个相等关系列出需要的代数式,进而列出两个方程,
组成方程
解:解所列方程组,得未知数的值
验:检验求得的值是否正确和符合实际情形
答:写出答案(包括单位名称)
创设情景,激发兴趣
如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
审题
2.已知的量:
3.要求的量:
1.运费的单位“元∕(吨·千米)”的含义
原料从A地运回工厂,每吨运费159元
产品从工厂运到B地,每吨运费162元
铁路、公路运费的单价
已知量与未知量的关系
原料的铁路运费+原料的公路运费=每吨原料的运费
产品的铁路运费+产品的公路运费=每吨产品的运费
解:设铁路运费为 元∕(吨·千米),公路运费为 元∕(吨·千米),依题意得:
答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米)
解方程组得:
整理方程组得:
解 设甲每天修公路x千米,乙每天修公路y千米,
答:甲每天修公路90千米,乙每天修公路30千米。
解得
根据题意,得
巩固练习:1、要修一段420千米长的公路,甲工程队先干2天乙工程队加入, 两队再合干2天完成任务;如果乙队先干2天,甲、乙两队再合干3天完成任务,问甲、乙两个工程队每天各能修路多少千米?
练习2.某药业集团生产的某种药品包装盒的侧面展开图如图,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得
解得:
cm3
答:这种药品包装盒的体积为135 cm3.
3、为了保护环境,某校环保小组成员收集废电池。第一天收集了1号电池4节,5号电池5节,总重量为460克,第二天收集1号电池2节,5号电池3节,总重量为240克,试问1号电池和5号电池每节分别重多少克?
课堂小结,知识梳理
1.列方程组解应用题的一般步骤
2.列表寻找应用题中的等量关系
8.3 实际问题与二元一次方程组
学习目标:
能分析实际问题中的数量关系,会设未知数,列方程组并求解,得到实际问题的答案,体会数学建模思想。
学习重点:
探究“二元一次方程组解决实际问题”。
探究1 养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940 kg。饲养员李大叔估计平均每只大牛1天约需饲料18~20 kg,每只小牛1天约需饲料7 ~8 kg。 你能否通过计算检验他的估计?
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中哪些是已知量,哪些是未知量?有几个等量关系?
问题3 如何解决这一问题?
解:设每头大牛和每头小牛1天分别约用饲料x kg、y kg,根据题意,得
列一元一次方程能解决这个问题吗?
请你解这个方程组,并交流一下你是如何解这个方程组的?
①
②
解:①×4-②×3,得
代入①,得
所以,方程组的解是
(1)在列方程组之前我们先做了哪些工作?
(2)列方程组解决实际问题的一般步骤是什么?
实际问题
设未知数、找等量关系、列方程(组)
数学问题
二元一次方程组
解方程(组)
数学问题的解
二元一次方程组的解
双检验
实际问题
的答案
你认为列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
① 能列二元一次方程组解决的实际问题,一般都可以通过列一元一次方程加以解决。但是,随着实际问题中未知量的增多和数量关系的复杂,列方程组将更加简单直接,因为问题有几个相等关系就可以列出几个方程。
② 两者相同点是都需要先分析题意,把实际问题转化为数学问题(设未知数,列方程或方程组),再检验解的合理性,进而得到实际问题的解,这一过程就是建模的过程。
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
100
200
设什么为未知数
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
x
y
E
F
列方程
x+y=200
甲总产量:乙总产量=3:4
总产量与什么有关
甲
100x
乙
200y
100x:200y=3:4
解:作EF⊥CB,交CB,AD于点F,E.设BF为x m,FC为y m.
200
100
例:据统计资料,甲、乙两种作物的单位面积产量的比是1:2 ,现要把一块长 200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4
A
B
C
D
x
y
E
F
甲
100x
乙
200y
解:作EF⊥CB,交CB,AD于点F,E.设BF为xm,FC为ym.
200
100
解得:
回顾交流
1、列方程组解应用题的步骤是什么?
审:审题,分析题中已知什么,求什么,明确各数量之间的关系
(找:找出能够表示应用题全部意义的两个相等关系)
设:设未知数(一般求什么,就设什么为x、y,注意单位)
列:根据这两个相等关系列出需要的代数式,进而列出两个方程,
组成方程
解:解所列方程组,得未知数的值
验:检验求得的值是否正确和符合实际情形
答:写出答案(包括单位名称)
创设情景,激发兴趣
如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
审题
2.已知的量:
3.要求的量:
1.运费的单位“元∕(吨·千米)”的含义
原料从A地运回工厂,每吨运费159元
产品从工厂运到B地,每吨运费162元
铁路、公路运费的单价
已知量与未知量的关系
原料的铁路运费+原料的公路运费=每吨原料的运费
产品的铁路运费+产品的公路运费=每吨产品的运费
解:设铁路运费为 元∕(吨·千米),公路运费为 元∕(吨·千米),依题意得:
答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米)
解方程组得:
整理方程组得:
解 设甲每天修公路x千米,乙每天修公路y千米,
答:甲每天修公路90千米,乙每天修公路30千米。
解得
根据题意,得
巩固练习:1、要修一段420千米长的公路,甲工程队先干2天乙工程队加入, 两队再合干2天完成任务;如果乙队先干2天,甲、乙两队再合干3天完成任务,问甲、乙两个工程队每天各能修路多少千米?
练习2.某药业集团生产的某种药品包装盒的侧面展开图如图,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.
解:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4)cm.根据题意,得
解得:
cm3
答:这种药品包装盒的体积为135 cm3.
3、为了保护环境,某校环保小组成员收集废电池。第一天收集了1号电池4节,5号电池5节,总重量为460克,第二天收集1号电池2节,5号电池3节,总重量为240克,试问1号电池和5号电池每节分别重多少克?
课堂小结,知识梳理
1.列方程组解应用题的一般步骤
2.列表寻找应用题中的等量关系
