人教版数学八年级下册 19.2.2 一次函数 课时3用待定系数法求一次函数解析式 课件(共15张)
文档属性
| 名称 | 人教版数学八年级下册 19.2.2 一次函数 课时3用待定系数法求一次函数解析式 课件(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 18:01:42 | ||
图片预览






文档简介
(共15张PPT)
人教版 八年级·下册
19.2.2 一次函数 课时3
第十九章 一次函数
时间:2022/5/10
用待定系数法求一次函数解析式
【思考】你在作一次函数图象时,分别描了几个点?
在上节课中我们学习了
一次函数解析式 图象及性质;反之,如果给你图象上的两点,能否求出函数的解析式呢?这将是本节课我们要研究的问题.
你为何选取这几个点?
导入新知
1.理解待定系数法的含义.
2. 学会运用待定系数法和数形结合思想求一次函数解析式.
素养目标
新知探究
例4 已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数 y=kx+b 的解析式,关键是求出 k、b 的值.从已知条件可以列出关于 k、b 的二元一次方程组,并求出 k、b.
知识点:待定系数法
这两点的坐标适合解析式
新知探究
解:设这个一次函数的解析式为 y=kx+b(k≠0)
∵ y=kx+b 的图象过点(3,5)与(-4,-9)
3k+b=5
-4k+b=-9
∴
∴ 这个一次函数的解析式为 y=2x-1.
k=2
b=-1
解得:
例4 已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
新知探究
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
由上面的例题你能归纳出求函数解析式的方法吗?
小结:在待定系数法确定函数解析式的时候,有几个未知数,就需要几个独立方程(条件).
新知探究
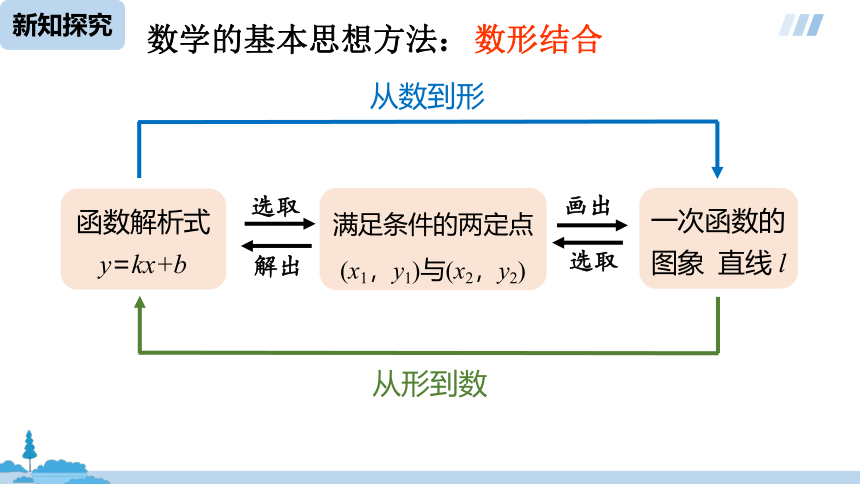
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象 直线 l
选取
解出
选取
画出
从数到形
从形到数
数学的基本思想方法:
数形结合
新知探究
用待定系数法求一次函数解析式的步骤
设:设出一次函数的解析式 y=kx+b(k≠0).
列:将已知的两组x、y的对应值分别代入所设的解析式 中,列出关于k、b的二元一次方程组.
解:解所列的方程组,求出k 、b的值.
代:将求出的k 、b的值代入所设解析式中,得到所求一次函数的解析式.
1
2
3
4
1.已知一次函数的图象经过两点(1,4)、( -1,0),求这个一次函数的解析式.
跟踪训练
解:设函数解析式为 y=kx+b
把两点(1,4),( -1,0 )代入得
k+b=4
-k+b=0
∴
k=2
b=2
解得:
∴ 函数解析式为 y=2x+2
2.已知一次函数y=kx+b(k≠0)经过(2,-1)和(-3,4)两点,则它的图象不经过第几象限?
随堂练习
解:把两点(2,-1)、( -3,4 )代入得
∴ 这个一次函数的解析式为 y=-x+1.
2k+b=-1
-3k+b=4
∴
k=-1
b=1
解得:
∴它的图象不经过第三象限
课堂小结
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
拓展提升
1.一次函数的图象经过点(2,1)且与直线 y=3x 平行,求此函数的解析式.
解: ∵一次函数与直线 y=3x 平行
∴设这个一次函数解析式为 y=3x+b
∵把点(2,1)代入得
∴ 6+b=1
解得: b=-5
∴ 这个一次函数的解析式为 y=3x-5.
2.已知一次函数图象经过点(2,3)和(-4,-9),求一次函数与 x 轴、y 轴的交点.
随堂练习
解:设这个一次函数解析式为y=kx+b(k≠0)
∵一次函数图象经过点(2,3)和( -4,-9 )
∴ 这个一次函数的解析式为 y=2x-1.
∴ y=2x-1 与 x 轴、y 轴的交点为( ,0 )、(0,-1).
2k+b=3
-4k+b=-9
∴
k=2
b=-1
解得:
拓展提升
3.已知一次函数 y=kx+4 的图象经过点(-3,-2).
解:(1)把点(-3,-2)代入 y=kx+4
则有:-3k+4=-2,解得:k=2
∴ 函数解析式为y=2x+4.
(1)求这个函数的解析式;(2)求函数图象与x轴、y轴的交点坐标.
课后作业
请完成课本后习题第1、2题。
人教版 八年级·下册
19.2.2 一次函数 课时3
第十九章 一次函数
时间:2022/5/10
用待定系数法求一次函数解析式
【思考】你在作一次函数图象时,分别描了几个点?
在上节课中我们学习了
一次函数解析式 图象及性质;反之,如果给你图象上的两点,能否求出函数的解析式呢?这将是本节课我们要研究的问题.
你为何选取这几个点?
导入新知
1.理解待定系数法的含义.
2. 学会运用待定系数法和数形结合思想求一次函数解析式.
素养目标
新知探究
例4 已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数 y=kx+b 的解析式,关键是求出 k、b 的值.从已知条件可以列出关于 k、b 的二元一次方程组,并求出 k、b.
知识点:待定系数法
这两点的坐标适合解析式
新知探究
解:设这个一次函数的解析式为 y=kx+b(k≠0)
∵ y=kx+b 的图象过点(3,5)与(-4,-9)
3k+b=5
-4k+b=-9
∴
∴ 这个一次函数的解析式为 y=2x-1.
k=2
b=-1
解得:
例4 已知一次函数的图象经过点(3,5)与(-4,-9),求这个一次函数的解析式.
一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
新知探究
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
由上面的例题你能归纳出求函数解析式的方法吗?
小结:在待定系数法确定函数解析式的时候,有几个未知数,就需要几个独立方程(条件).
新知探究
函数解析式
y=kx+b
满足条件的两定点(x1,y1)与(x2,y2)
一次函数的图象 直线 l
选取
解出
选取
画出
从数到形
从形到数
数学的基本思想方法:
数形结合
新知探究
用待定系数法求一次函数解析式的步骤
设:设出一次函数的解析式 y=kx+b(k≠0).
列:将已知的两组x、y的对应值分别代入所设的解析式 中,列出关于k、b的二元一次方程组.
解:解所列的方程组,求出k 、b的值.
代:将求出的k 、b的值代入所设解析式中,得到所求一次函数的解析式.
1
2
3
4
1.已知一次函数的图象经过两点(1,4)、( -1,0),求这个一次函数的解析式.
跟踪训练
解:设函数解析式为 y=kx+b
把两点(1,4),( -1,0 )代入得
k+b=4
-k+b=0
∴
k=2
b=2
解得:
∴ 函数解析式为 y=2x+2
2.已知一次函数y=kx+b(k≠0)经过(2,-1)和(-3,4)两点,则它的图象不经过第几象限?
随堂练习
解:把两点(2,-1)、( -3,4 )代入得
∴ 这个一次函数的解析式为 y=-x+1.
2k+b=-1
-3k+b=4
∴
k=-1
b=1
解得:
∴它的图象不经过第三象限
课堂小结
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
拓展提升
1.一次函数的图象经过点(2,1)且与直线 y=3x 平行,求此函数的解析式.
解: ∵一次函数与直线 y=3x 平行
∴设这个一次函数解析式为 y=3x+b
∵把点(2,1)代入得
∴ 6+b=1
解得: b=-5
∴ 这个一次函数的解析式为 y=3x-5.
2.已知一次函数图象经过点(2,3)和(-4,-9),求一次函数与 x 轴、y 轴的交点.
随堂练习
解:设这个一次函数解析式为y=kx+b(k≠0)
∵一次函数图象经过点(2,3)和( -4,-9 )
∴ 这个一次函数的解析式为 y=2x-1.
∴ y=2x-1 与 x 轴、y 轴的交点为( ,0 )、(0,-1).
2k+b=3
-4k+b=-9
∴
k=2
b=-1
解得:
拓展提升
3.已知一次函数 y=kx+4 的图象经过点(-3,-2).
解:(1)把点(-3,-2)代入 y=kx+4
则有:-3k+4=-2,解得:k=2
∴ 函数解析式为y=2x+4.
(1)求这个函数的解析式;(2)求函数图象与x轴、y轴的交点坐标.
课后作业
请完成课本后习题第1、2题。
