沪科版数学八年级下册 19.3.7正方形的概念及性质 课件(共22张)
文档属性
| 名称 | 沪科版数学八年级下册 19.3.7正方形的概念及性质 课件(共22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1019.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 18:03:29 | ||
图片预览



文档简介
(共22张PPT)
19.3.7 正方形及其性质
课题导入
课题导入
1.理解正方形定义,并了解平行四边形、矩形、菱形之间的联系和区别.
2.掌握正方形的性质,能运用正方形性质解决相关的问题.
目标引领
菱形
矩形
正方形
平行四边形
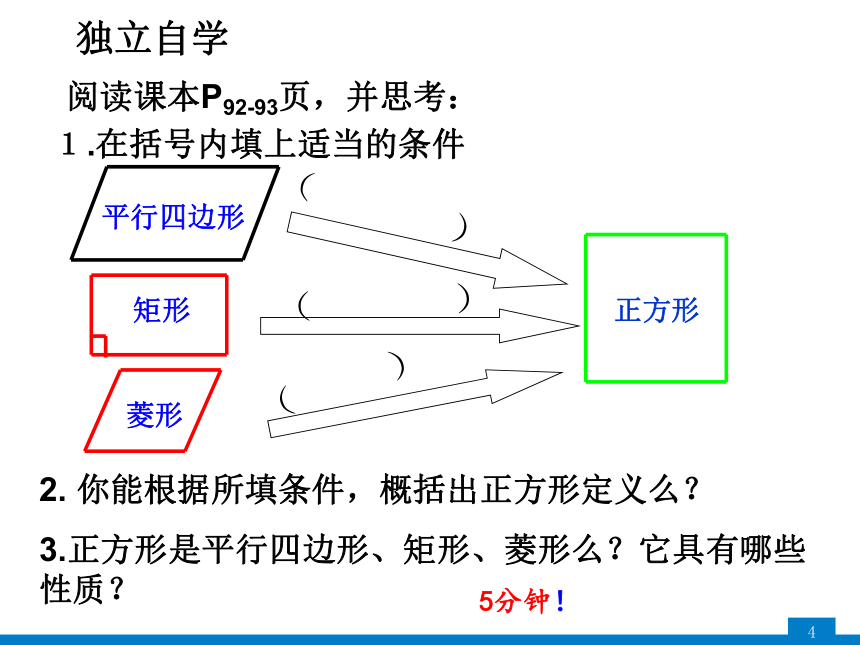
阅读课本P92-93页,并思考:
( )
( )
( )
2. 你能根据所填条件,概括出正方形定义么?
3.正方形是平行四边形、矩形、菱形么?它具有哪些性质?
1.在括号内填上适当的条件
独立自学
5分钟!
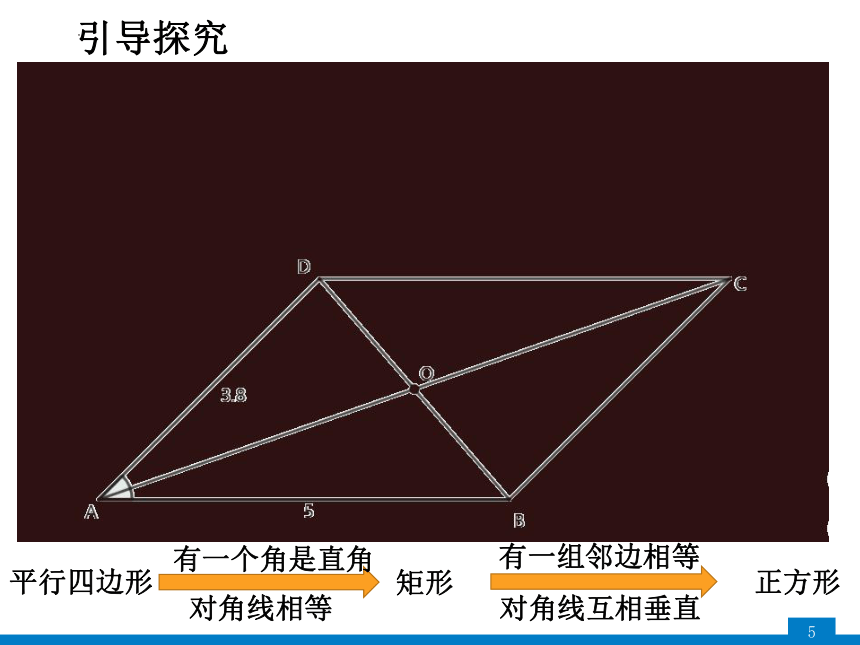
引导探究
平行四边形
矩形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
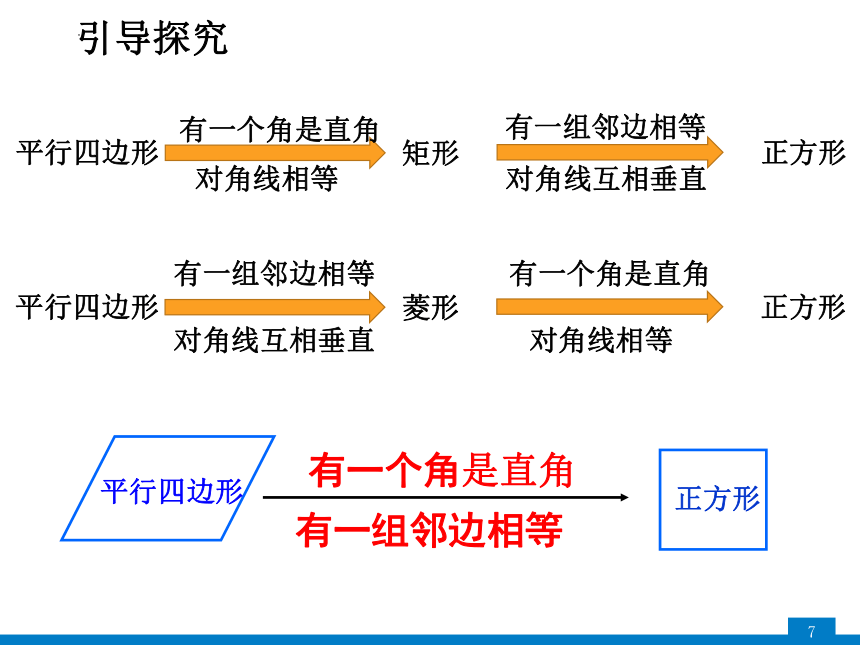
引导探究
平行四边形
菱形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
平行四边形
矩形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
引导探究
平行四边形
菱形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
有一组邻边相等
有一个角是直角
平行四边形
正方形
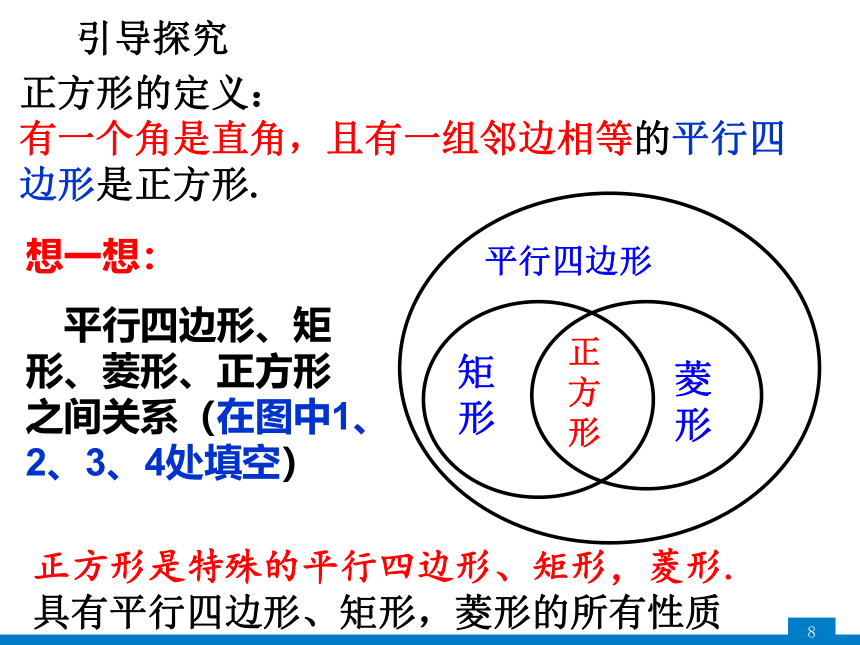
正方形的定义:
有一个角是直角,且有一组邻边相等的平行四边形是正方形.
引导探究
想一想:
平行四边形、矩形、菱形、正方形之间关系(在图中1、2、3、4处填空)
1
2
3
4
矩
形
菱
形
正方形
平行四边形
正方形是特殊的平行四边形、矩形,菱形.具有平行四边形、矩形,菱形的所有性质
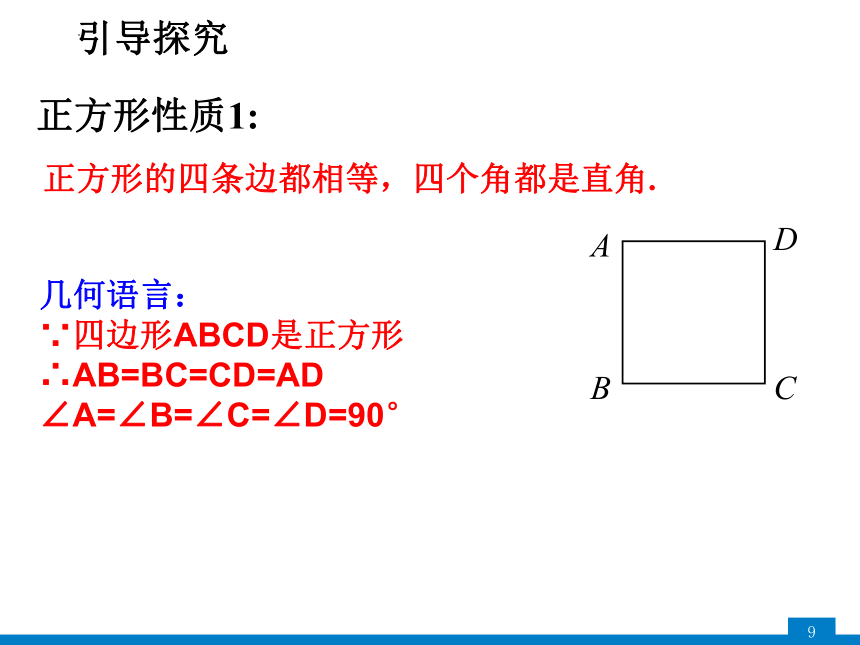
正方形性质1:
正方形的四条边都相等,四个角都是直角.
引导探究
A
B
C
D
几何语言:
∵四边形ABCD是正方形
∴AB=BC=CD=AD
∠A=∠B=∠C=∠D=90°
正方形性质2:
正方形的对角线相等且互相垂直平分.
引导探究
几何语言:
∵四边形ABCD是正方形
∴AC=BD且AC⊥BD
A
B
C
D
O
注:对角线把正方形分成四个全等的等腰直角三角形
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考. 正方形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
引导探究
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
引导探究
3.如图,已知正方形ABCD,以AB为边向
正方形外作等边三角形ABE,连结DE、
CE,则∠DEA=_____ ,∠DEC=_____
15°
30°
引导探究
引导探究
4.在正方形ABCD中:已知,如图,点E、F分别在BC、CD上,且AE⊥BF,垂足为M.
求证:AE=BF.
一线三垂直模型
(“十字模型”)
N
引导探究
一线三垂直模型
变式1:在正方形ABCD中:如图,如果点E、F、G分别在BC、CD、DA上,且GE⊥BF,垂足M.
求证:GE=BF.
变式2:如图,在正方形ABCD中,F为BC延长线上一点,E为CD边上一点,CE=CF,BE的延长线交DF于点G.
(1)求证:BG⊥DF
(2)若∠BEC=60°,求∠EFD度数.
引导探究
一线三垂直模型
5.如图,点P是正方形ABCD对角线AC上的任意一点,连接BP,DP,求证BP=DP.
引导探究
若点P在直线AC上,结论是否成立.
正方形(或菱形)一条对角线所在直线上的点,到另外两个顶点的距离相等(两组全等三角形)
引导探究
变式1:如图,点P是正方形ABCD对角线AC上的任意一点,过点P作相邻两边的垂线.
求证:(1)PE=PF=DH,PH=PG=BF
(2)矩形DEPH和矩形PFBG面积相等
变式2:如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,求AF的长.
引导探究
正方形对角线上的点,辅助线常向正方形的边作垂直
你有什么收获或疑惑?
目标升华
2.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
1.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
16cm
P
A
B
C
D
E
F
O
M
A
B
C
D
E
F
O
(选做)如图,四边形ABCD和DEFG都是正方形
求证:AE=CG
A
B
C
D
E
F
G
当堂诊学
1、课后练习1、2、3、4;
2、预习
强化补清
19.3.7 正方形及其性质
课题导入
课题导入
1.理解正方形定义,并了解平行四边形、矩形、菱形之间的联系和区别.
2.掌握正方形的性质,能运用正方形性质解决相关的问题.
目标引领
菱形
矩形
正方形
平行四边形
阅读课本P92-93页,并思考:
( )
( )
( )
2. 你能根据所填条件,概括出正方形定义么?
3.正方形是平行四边形、矩形、菱形么?它具有哪些性质?
1.在括号内填上适当的条件
独立自学
5分钟!
引导探究
平行四边形
矩形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
引导探究
平行四边形
菱形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
平行四边形
矩形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
引导探究
平行四边形
菱形
正方形
有一个角是直角
对角线相等
有一组邻边相等
对角线互相垂直
有一组邻边相等
有一个角是直角
平行四边形
正方形
正方形的定义:
有一个角是直角,且有一组邻边相等的平行四边形是正方形.
引导探究
想一想:
平行四边形、矩形、菱形、正方形之间关系(在图中1、2、3、4处填空)
1
2
3
4
矩
形
菱
形
正方形
平行四边形
正方形是特殊的平行四边形、矩形,菱形.具有平行四边形、矩形,菱形的所有性质
正方形性质1:
正方形的四条边都相等,四个角都是直角.
引导探究
A
B
C
D
几何语言:
∵四边形ABCD是正方形
∴AB=BC=CD=AD
∠A=∠B=∠C=∠D=90°
正方形性质2:
正方形的对角线相等且互相垂直平分.
引导探究
几何语言:
∵四边形ABCD是正方形
∴AC=BD且AC⊥BD
A
B
C
D
O
注:对角线把正方形分成四个全等的等腰直角三角形
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考. 正方形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
引导探究
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
引导探究
3.如图,已知正方形ABCD,以AB为边向
正方形外作等边三角形ABE,连结DE、
CE,则∠DEA=_____ ,∠DEC=_____
15°
30°
引导探究
引导探究
4.在正方形ABCD中:已知,如图,点E、F分别在BC、CD上,且AE⊥BF,垂足为M.
求证:AE=BF.
一线三垂直模型
(“十字模型”)
N
引导探究
一线三垂直模型
变式1:在正方形ABCD中:如图,如果点E、F、G分别在BC、CD、DA上,且GE⊥BF,垂足M.
求证:GE=BF.
变式2:如图,在正方形ABCD中,F为BC延长线上一点,E为CD边上一点,CE=CF,BE的延长线交DF于点G.
(1)求证:BG⊥DF
(2)若∠BEC=60°,求∠EFD度数.
引导探究
一线三垂直模型
5.如图,点P是正方形ABCD对角线AC上的任意一点,连接BP,DP,求证BP=DP.
引导探究
若点P在直线AC上,结论是否成立.
正方形(或菱形)一条对角线所在直线上的点,到另外两个顶点的距离相等(两组全等三角形)
引导探究
变式1:如图,点P是正方形ABCD对角线AC上的任意一点,过点P作相邻两边的垂线.
求证:(1)PE=PF=DH,PH=PG=BF
(2)矩形DEPH和矩形PFBG面积相等
变式2:如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上,BF⊥EF,CE=1,求AF的长.
引导探究
正方形对角线上的点,辅助线常向正方形的边作垂直
你有什么收获或疑惑?
目标升华
2.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
1.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
16cm
P
A
B
C
D
E
F
O
M
A
B
C
D
E
F
O
(选做)如图,四边形ABCD和DEFG都是正方形
求证:AE=CG
A
B
C
D
E
F
G
当堂诊学
1、课后练习1、2、3、4;
2、预习
强化补清
