人教版数学八年级下册 第17章 小结与复习 课件(共23张)
文档属性
| 名称 | 人教版数学八年级下册 第17章 小结与复习 课件(共23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 19:12:40 | ||
图片预览






文档简介
(共24张PPT)
小结与复习
第十七章 勾股定理
学习目标
【学习目标】
1.理清本章的知识结构和重要知识点.
2.掌握本章的重要解题技巧.
【学习重点】
勾股定理及其逆定理的应用.
【学习难点】
利用勾股定理及其逆定理解决实际问题.
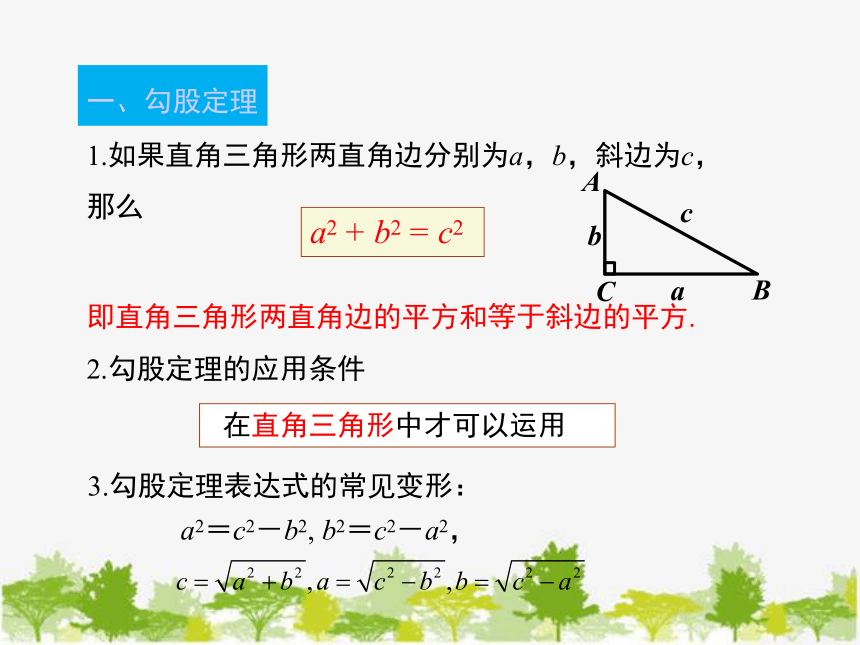
1.如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
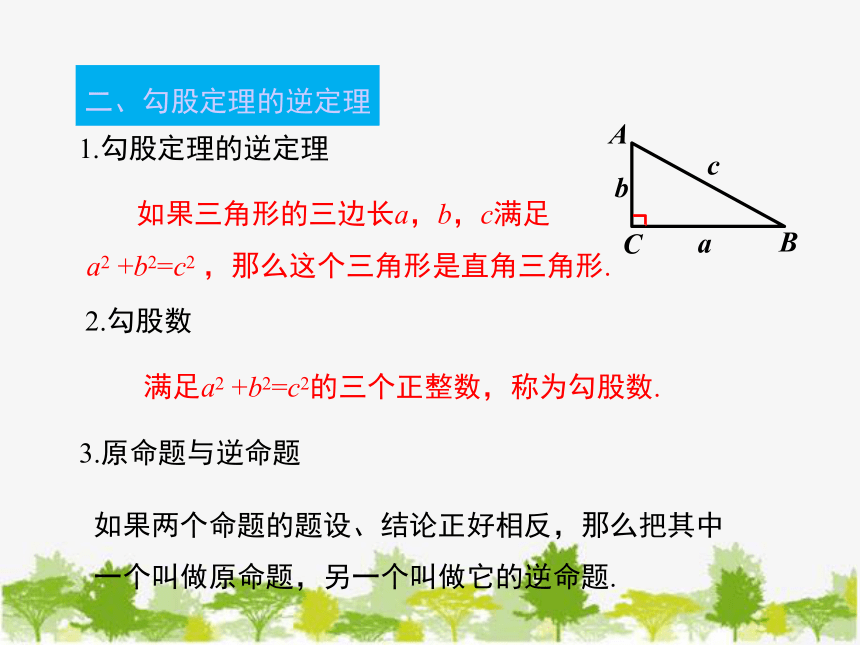
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
例1 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
【解析】这是在三角形中已知两边长求高的问题,可用勾股定理先求出第三边再求解.
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b BD= ac,
A
C
B
4
3
D
考点一 勾股定理及其应用
在直角三角形中,已知两边的长求斜边上的高时,先用勾股定理求出第三边,然后用面积求斜边上的高较为简便.在用勾股定理时,一定要清楚直角所对的边才是斜边,如在本例中不要受勾股数3,4,5的干扰.
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
针对训练
D
方法总结
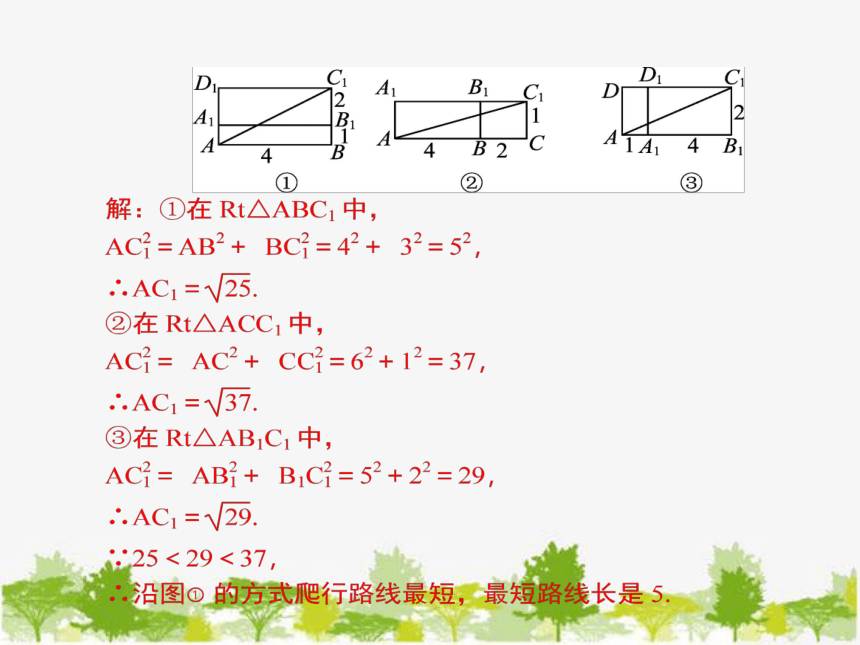
例2 如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
【解析】蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:①沿
ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
用勾股定理解决立体图形的问题,常以长方体、正方体、圆柱、圆锥为背景,做题思路是“展曲为平” ——把立体图形转化为平面图形,即将原图形的侧面展开转化为平面图形问题,再运用“平面上的两点之间线段最短”求解.
要注意的是需要认真审题,确定出最短路线,有时容易忽视多种展开情况.
方法总结
1.如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
D
A. B. C. D.5
针对训练
例3 已如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
【解析】由题意知AB=DE=25米,BC=7米,AD=4米,
∵在直角△ABC中,AC为直角边,
∴AC= =24米,
已知AD=4米,则CD=24-4=20(米),
∵在直角△CDE中,CE为直角边,
∴CE= =15(米),
BE=15-7=8(米).故选C.
A.4米 B.6米 C.8米 D.10米
C
3.如图,某住宅社区在相邻两楼之间修建一个上方是一个
半圆,下方是长方形的仿古通道,现有一辆卡车装满家
具后,高4米,宽2.8米,请问这辆送家具的卡车能否通
过这个通道?
针对训练
在Rt△ABO中,由题意知OA=2米,DC=OB=1.4米,
所以AB2=22-1.42=2.04.
因为4-2.6=1.4,1.42=1.96,
2.04>1.96,
所以卡车可以通过.
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
例1 已知在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,a=n2-1,b=2n,c=n2+1(n>1),判断△ABC是否为直角三角形.
【解析】要证∠C=90°,只要证△ABC是直角三角形,并且c边最大.根据勾股定理的逆定理只要证明a2+b2=c2即可.
解:由于a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2
=n4+2n2+1,从而a2+b2=c2,故可以判定△ABC是
直角三角形.
考点二 勾股定理的逆定理及其应用
运用勾股定理的逆定理判断一个三角形是否是直角三角形的一般步骤:①先判断哪条边最大;②分别用代数方法计算出a2+b2和c2的值(c边最大);③判断a2+b2和c2是否相等,若相等,则是直角三角形;若不相等,则不是直角三角形.
方法总结
1.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6 C.3,4,5 D.7,8,9
2.已知下列图形中的三角形的顶点都在正方形的格点 上,可以判定三角形是直角三角形的有________.
(2)(4)
C
针对训练
例2 B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8 n mile的速度前进,乙船沿南偏东某个角度以每小时15 n mile的速度前进,2 h后,甲船到M岛,乙船到P岛,两岛相距34 n mile,你知道乙船是沿哪个方向航行的吗?
解:甲船航行的距离为BM= 16(n mile),
乙船航行的距离为BP= 30(n mile).
∵162+302=1156,342=1156,
∴BM2+BP2=MP2,
∴△MBP为直角三角形,∴∠MBP=90° ,
∴乙船是沿着南偏东30°方向航行的.
6.如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.则这块地
的面积为 .
A
B
C
3
4
13
12
D
解析:连接AC.由AD=4m,CD=3m,∠ADC=90°,可得AC=5m.再由AB=13m,BC=12m,可知△ABC是直角三角形.于是这块地的面积为(12×5-3×4)÷2=24(cm2)
24cm2
针对训练
例3 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
问题:1.由AB=8,BC=10,你可以知道哪些线段长?
2.在Rt△DFC中,你可以求出DF的长吗?
3.由DF的长,你还可以求出哪条线段长?
4.设BE = x,你可以用含有x的式子表示出哪些线段长?
考点三 勾股定理与折叠问题
解:由折叠可知FC=BC=10,BE=FE.
在长方形ABCD中,DC=AB=8 ,
AD=BC=10,∠D=90°.
∴DF=6, AF=4.
设BE=FE=x,则AE=8-x .
在Rt△AFE中,由勾股定理得
∴ ,解得 x = 5 .
∴BE的长为5.
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
7.如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕是DE,则CD的长为 .
1.75cm
针对训练
方法总结
通过今天的学习,
能说说你的收获和体会吗
你有什么经验与收获让同学们共享呢?
回顾反思
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
课堂小结
小结与复习
第十七章 勾股定理
学习目标
【学习目标】
1.理清本章的知识结构和重要知识点.
2.掌握本章的重要解题技巧.
【学习重点】
勾股定理及其逆定理的应用.
【学习难点】
利用勾股定理及其逆定理解决实际问题.
1.如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
2.勾股定理的应用条件
一、勾股定理
3.勾股定理表达式的常见变形:
a2=c2-b2, b2=c2-a2,
A
B
C
c
a
b
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
例1 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
【解析】这是在三角形中已知两边长求高的问题,可用勾股定理先求出第三边再求解.
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b BD= ac,
A
C
B
4
3
D
考点一 勾股定理及其应用
在直角三角形中,已知两边的长求斜边上的高时,先用勾股定理求出第三边,然后用面积求斜边上的高较为简便.在用勾股定理时,一定要清楚直角所对的边才是斜边,如在本例中不要受勾股数3,4,5的干扰.
1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
针对训练
D
方法总结
例2 如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
【解析】蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:①沿
ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
用勾股定理解决立体图形的问题,常以长方体、正方体、圆柱、圆锥为背景,做题思路是“展曲为平” ——把立体图形转化为平面图形,即将原图形的侧面展开转化为平面图形问题,再运用“平面上的两点之间线段最短”求解.
要注意的是需要认真审题,确定出最短路线,有时容易忽视多种展开情况.
方法总结
1.如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
D
A. B. C. D.5
针对训练
例3 已如图,一架云梯25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
【解析】由题意知AB=DE=25米,BC=7米,AD=4米,
∵在直角△ABC中,AC为直角边,
∴AC= =24米,
已知AD=4米,则CD=24-4=20(米),
∵在直角△CDE中,CE为直角边,
∴CE= =15(米),
BE=15-7=8(米).故选C.
A.4米 B.6米 C.8米 D.10米
C
3.如图,某住宅社区在相邻两楼之间修建一个上方是一个
半圆,下方是长方形的仿古通道,现有一辆卡车装满家
具后,高4米,宽2.8米,请问这辆送家具的卡车能否通
过这个通道?
针对训练
在Rt△ABO中,由题意知OA=2米,DC=OB=1.4米,
所以AB2=22-1.42=2.04.
因为4-2.6=1.4,1.42=1.96,
2.04>1.96,
所以卡车可以通过.
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
例1 已知在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,a=n2-1,b=2n,c=n2+1(n>1),判断△ABC是否为直角三角形.
【解析】要证∠C=90°,只要证△ABC是直角三角形,并且c边最大.根据勾股定理的逆定理只要证明a2+b2=c2即可.
解:由于a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2
=n4+2n2+1,从而a2+b2=c2,故可以判定△ABC是
直角三角形.
考点二 勾股定理的逆定理及其应用
运用勾股定理的逆定理判断一个三角形是否是直角三角形的一般步骤:①先判断哪条边最大;②分别用代数方法计算出a2+b2和c2的值(c边最大);③判断a2+b2和c2是否相等,若相等,则是直角三角形;若不相等,则不是直角三角形.
方法总结
1.下列各组数中,是勾股数的为( )
A.1,2,3 B.4,5,6 C.3,4,5 D.7,8,9
2.已知下列图形中的三角形的顶点都在正方形的格点 上,可以判定三角形是直角三角形的有________.
(2)(4)
C
针对训练
例2 B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8 n mile的速度前进,乙船沿南偏东某个角度以每小时15 n mile的速度前进,2 h后,甲船到M岛,乙船到P岛,两岛相距34 n mile,你知道乙船是沿哪个方向航行的吗?
解:甲船航行的距离为BM= 16(n mile),
乙船航行的距离为BP= 30(n mile).
∵162+302=1156,342=1156,
∴BM2+BP2=MP2,
∴△MBP为直角三角形,∴∠MBP=90° ,
∴乙船是沿着南偏东30°方向航行的.
6.如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m.则这块地
的面积为 .
A
B
C
3
4
13
12
D
解析:连接AC.由AD=4m,CD=3m,∠ADC=90°,可得AC=5m.再由AB=13m,BC=12m,可知△ABC是直角三角形.于是这块地的面积为(12×5-3×4)÷2=24(cm2)
24cm2
针对训练
例3 已知如图,将长方形的一边BC沿CE折叠,
使得点B落在AD边的点F处,已知AB=8,
BC=10, 求BE的长.
问题:1.由AB=8,BC=10,你可以知道哪些线段长?
2.在Rt△DFC中,你可以求出DF的长吗?
3.由DF的长,你还可以求出哪条线段长?
4.设BE = x,你可以用含有x的式子表示出哪些线段长?
考点三 勾股定理与折叠问题
解:由折叠可知FC=BC=10,BE=FE.
在长方形ABCD中,DC=AB=8 ,
AD=BC=10,∠D=90°.
∴DF=6, AF=4.
设BE=FE=x,则AE=8-x .
在Rt△AFE中,由勾股定理得
∴ ,解得 x = 5 .
∴BE的长为5.
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
7.如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕是DE,则CD的长为 .
1.75cm
针对训练
方法总结
通过今天的学习,
能说说你的收获和体会吗
你有什么经验与收获让同学们共享呢?
回顾反思
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
课堂小结
