北师大版数学七年级下册 1.5.1平方差公式 课件(共15张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 1.5.1平方差公式 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 00:00:00 | ||
图片预览




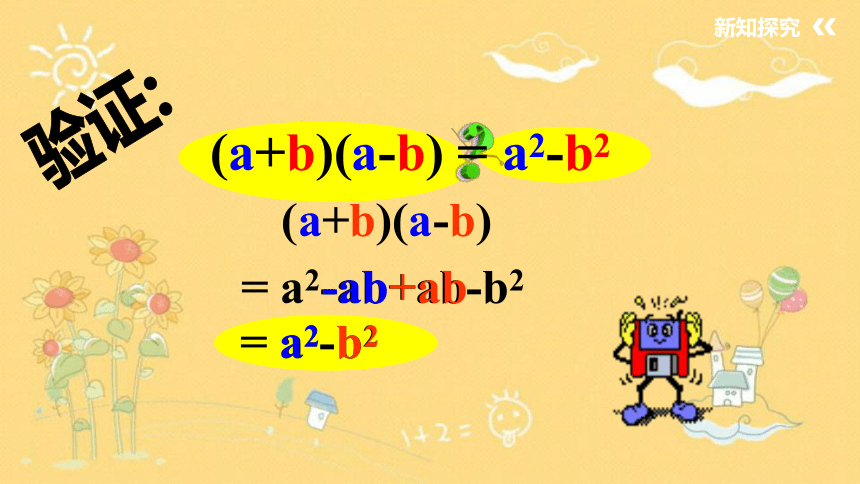

文档简介
(共15张PPT)
平方差公式
情境引入
小霞同学去商店买了单价10.2元/千克的糖果9.8千克,小霞同学马上说:“应付99.96元。”售货员很惊讶:“你真是个神童!”小霞同学说:“过奖了,我只是利用了数学上刚学过的一个公式而已!”
学习目标
1、会判断一个式子能否采用平方差公式计算.
2、能说出平方差公式的结构特征.
3、会运用平方差公式进行简单整式乘法的运算.
新知探究
规律探索:
计算下列多项式的积:
(x+1)(x-1) =
(m-2)(m+2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
你发现了什么?
新知探究
(a+b)(a-b) = a2-b2
验证:
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
新知探究
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
新知探究
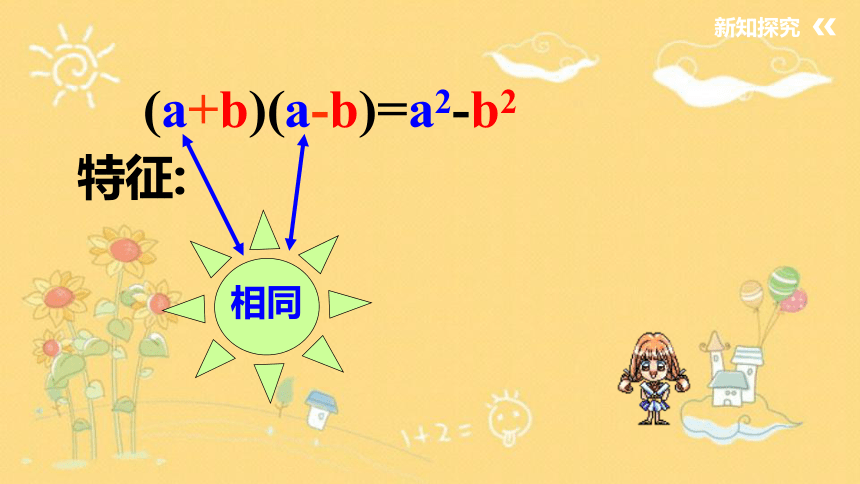
(a+b)(a-b)=a2-b2
特征:
相同
新知探究
(a+b)(a-b)=a2-b2
特征:
相反数
新知探究
(a+b)(a-b)=a2-b2
特征:
相同项的平方 - 相反项的平方
新知探究
(a+b)(a-b)=a2-b2
平方差公式特征:
(1)左边括号中有两项完全相同,两项互为相反数.
(2)右边是相同项的平方减去相反项的平方.
(3)公式中的a,b可以表示 一个单项式也可以表示一个多项式.
新知探究
判断
判断下列各式能否用平方差公式运算
1.(b-8)(b+8) 2.(-x-1)(x+1)
3.(x+3)(x-2) 4.(mn-4k)(-mn-4k)
新知探究
例1 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
(2) (-x+2y)(-x-2y).
小试身手
运用平方差公式计算:
(1) (a+3b)(a-3b)
(2) (3+2a)(-3+2a)
小试身手
用平方差公式计算
注意:(1)(2)任选一题
(3)(4)任选一题
运用公式前,
首先要判断
哪两项相同,
哪两项互为相反数。
课堂小结
二、运用平方差公式的关键:找到公式中的a和b.
技巧:
1、判—找出相同项(公式中的a)和相反项(公式中的b);
2、套—利用公式计算。
一、了解平方差公式的特点:
(1)左边括号中有两项完全相同,两项互为相反数.
(2)右边是相同项的平方减去相反项的平方.
平方差公式
情境引入
小霞同学去商店买了单价10.2元/千克的糖果9.8千克,小霞同学马上说:“应付99.96元。”售货员很惊讶:“你真是个神童!”小霞同学说:“过奖了,我只是利用了数学上刚学过的一个公式而已!”
学习目标
1、会判断一个式子能否采用平方差公式计算.
2、能说出平方差公式的结构特征.
3、会运用平方差公式进行简单整式乘法的运算.
新知探究
规律探索:
计算下列多项式的积:
(x+1)(x-1) =
(m-2)(m+2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
你发现了什么?
新知探究
(a+b)(a-b) = a2-b2
验证:
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
新知探究
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
新知探究
(a+b)(a-b)=a2-b2
特征:
相同
新知探究
(a+b)(a-b)=a2-b2
特征:
相反数
新知探究
(a+b)(a-b)=a2-b2
特征:
相同项的平方 - 相反项的平方
新知探究
(a+b)(a-b)=a2-b2
平方差公式特征:
(1)左边括号中有两项完全相同,两项互为相反数.
(2)右边是相同项的平方减去相反项的平方.
(3)公式中的a,b可以表示 一个单项式也可以表示一个多项式.
新知探究
判断
判断下列各式能否用平方差公式运算
1.(b-8)(b+8) 2.(-x-1)(x+1)
3.(x+3)(x-2) 4.(mn-4k)(-mn-4k)
新知探究
例1 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
(2) (-x+2y)(-x-2y).
小试身手
运用平方差公式计算:
(1) (a+3b)(a-3b)
(2) (3+2a)(-3+2a)
小试身手
用平方差公式计算
注意:(1)(2)任选一题
(3)(4)任选一题
运用公式前,
首先要判断
哪两项相同,
哪两项互为相反数。
课堂小结
二、运用平方差公式的关键:找到公式中的a和b.
技巧:
1、判—找出相同项(公式中的a)和相反项(公式中的b);
2、套—利用公式计算。
一、了解平方差公式的特点:
(1)左边括号中有两项完全相同,两项互为相反数.
(2)右边是相同项的平方减去相反项的平方.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
