1.2数据结构(2课时)课件 2021—2022学年高中信息技术浙教版(2019)选修1(49张PPT)
文档属性
| 名称 | 1.2数据结构(2课时)课件 2021—2022学年高中信息技术浙教版(2019)选修1(49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-05-11 00:00:00 | ||
图片预览









文档简介
(共49张PPT)
CHZX
1.2 数据的组织
浙江省高中信息技术 选择性必修一 《数据与数据结构》
数据结构的概念
数据元素
数据类型
数据结构
01
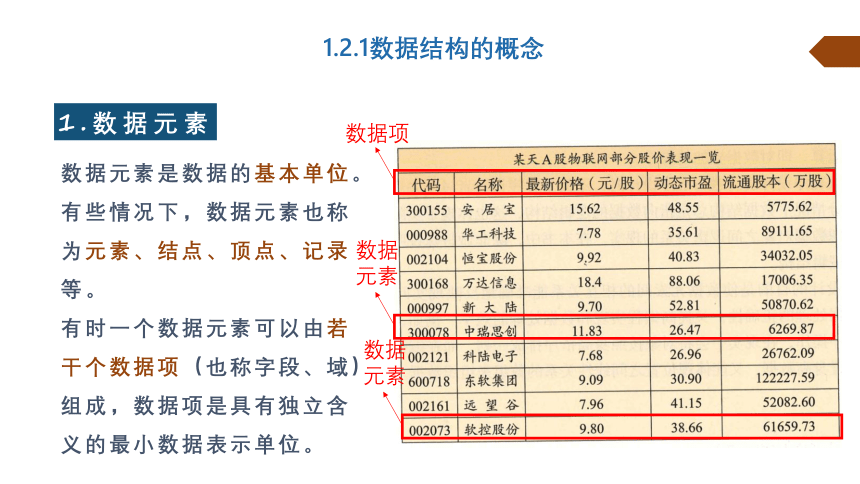
1.数据元素
数据元素是数据的基本单位。有些情况下,数据元素也称为元素、结点、顶点、记录等。
有时一个数据元素可以由若干个数据项(也称字段、域)组成,数据项是具有独立含义的最小数据表示单位。
1.2.1数据结构的概念
数据项
数据元素
数据元素
1.数据元素
Q1:这张表一共有多少个数据元素?
1.2.1数据结构的概念
10个
Q2:第三个数据元素的第三个数据项的名称为什么?值为什么?
最新价格(元/股)9.92
2.数据类型
数据类型指的是具有相同性质的计算机数据的集合及在这个数据集合上的一组操作。数据类型可以分为基本数据类型(也称为原子数据类型)和结构数据类型。
1.2.1数据结构的概念
基本数据类型由计算机编程环境提供,编程者可以在编程时直接用系统提供的标识符进行定义,如Python编程语言中的整型、实型、布尔型等。
结构数据类型是在程序设计时利用基本数据类型构造出的、复合的新类型,这种新类型由用户根据实际需要定义,能较好地描述数据元素数据项组成以及数据元素之间的逻辑关系,方便用户根据数据之间逻辑关系的特点进行数据处理,如很多编程语言中提供的记录类型、集合等。
基本数据类型
结构数据类型
3.数据结构
数据结构指的是数据之间的相互关系,即数据的组织形式。它包括了以下三个方面的内容:
①数据元素之间的逻辑关系,也称为数据的逻辑结构。
②数据元素及其关系在计算机存储器内的表示,也称为数据的存储结构或物理结构。
③数据的运算,即对数据施加的操作。
1.2.1数据结构的概念
课堂练习
B
B
常见的数据结构
数组
链表
队列
栈
树
02
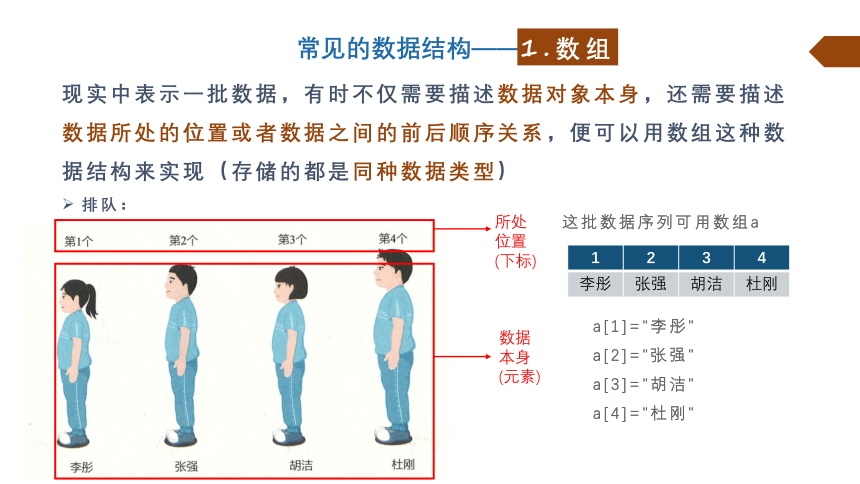
现实中表示一批数据,有时不仅需要描述数据对象本身,还需要描述数据所处的位置或者数据之间的前后顺序关系,便可以用数组这种数据结构来实现(存储的都是同种数据类型)
排队:
常见的数据结构——数组
这批数据序列可用数组a
1.数组
所处位置
(下标)
数据本身
(元素)
1 2 3 4
李彤 张强 胡洁 杜刚
a[1]="李彤"
a[2]="张强"
a[3]="胡洁"
a[4]="杜刚"
常见的数据结构——数组
1.数组
也可以通过变量名后面的下标依次按顺序遍历序列中的每个元素。
例:用sg数组来存放身高信息,sg=[165,169,185,179,172,191]
sg[0]=165(下标从0开始)
用数组组织数据时,可以快速通过下标精准地访问序列中的某个元素
方法一:
sg=[165,169,185,179,172,191]
for i in range(6):
print(sg[i])
方法二:
sg=[165,169,185,179,172,191]
for i in sg:
print(i)
常见的数据结构——数组
1.数组
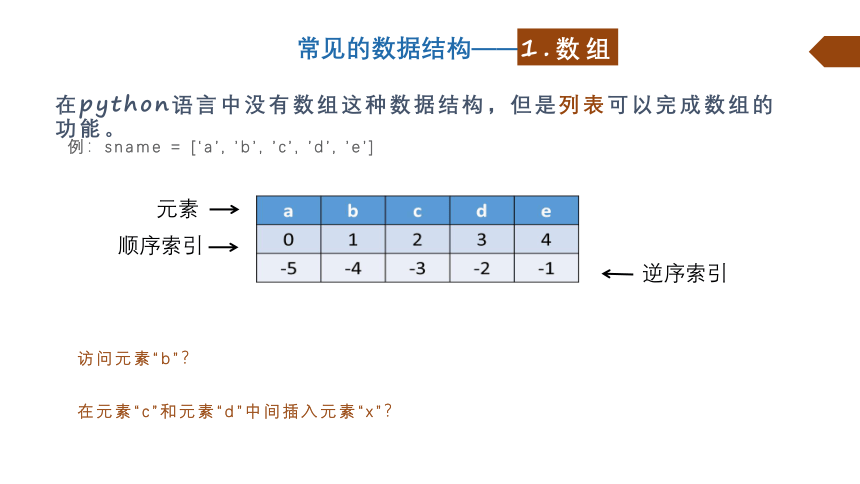
例:sname = [‘a’, ’b’, ’c’, ’d’, ’e’]
在python语言中没有数组这种数据结构,但是列表可以完成数组的功能。
元素
顺序索引
逆序索引
访问元素“b”?
在元素“c”和元素“d”中间插入元素“x”?
问题一:现实生活中,有哪些数据适合用数组来存储?
问题与讨论?
特点:同种数据类型
超市商品的价格
统计全班同学的生日
杭州到全国各省会城市的机票价格
……
问题二:排队时,你是如何记住自己的位置的?
常见的数据结构——数组
2.链表
吴坚知道自己排在首位,王林知道排在自己前面的是吴坚,黄刚知道排在自己前面的是王林,李丰知道排在自己前面的是黄刚。有了这些相邻人员之间的链接关系,即使休息时大家分散在各处,一旦需要集合,大家可以根据链接关系快速地按照原顺序排成队伍。虽然整队前后每个人员的站位地点发生改变,但相互之间排队的顺序关系是不变的。
常见的数据结构——数组
2.链表
抽象化后的排队链接关系
组织、处理一批数据时,若不关心数据实际所处的具体位置,而只需知道数据之间相互链接的顺序时,可以借鉴上面的方法。在计算机科学中,这种方法的具体实现形式就是链表。
常见的数据结构——数组
2.链表
单向链表
头节点,便可以从head指向的头节点开始依次遍历链表中的每个节点
思考:该链表的指针指向的是前面还是后面?
常见的数据结构——数组
2.链表
链表内存存放方式:
head
(头节点)
tail
None
数据域
指针域
My_list
基本元素:
(1)节点:每个节点有两个部分,左边称为数值域,存放用户数据;右边部分称为指针域,用来存放指向下一个元素的指针(地址)。
(2)head:head节点永远指向第一个节点
(3)tail:tail永远指向最后一个节点
(4)None:链表中最后一个节点的指针域为None值
常见的数据结构——数组
2.链表
单向链表
双向链表
单链表的基础上,增加一个指向前趋节点的链接
基于单向链表的循环链表
单链表的基础上,在链表的首尾之间增加链接
问题与讨论?
何为单向链表、双向链表、基于单向链表的循环链表?
单向链表
双向链表
基于单向链表的循环链表
问题与讨论?
数组的特点?
不仅需要描述数据对象本身,还需要描述数据所处的位置或者数据之间的前后顺序关系
链表的特点?
只需知道数据之间相互链接的顺序
在数组中插入元素和在链表中插入元素的差别?
数组:整体后移空出位置插入
链表:改变指针
常见的数据结构——数组
3.队列
有序排队上车的乘客
有序排队接客的出租车
乘客排队时先到的总是从队伍的头部出去(出队)上车,而后到的乘客则必须在队伍的尾部加入(入队)。同时,为了确保有序,人们总是规定不能从队伍的中间部位插队。
常见的数据结构——数组
3.队列
概 念:队列是一种先进先出的线性表,允许插入的一端称为队尾,允许删除的一端称为队首
队列元素:队列中的数据元素。
入 队:在队列中插入一个元素的过程。
出 队:从队列中删除一个元素的过程。
出队
入队
队首元素
队尾元素
常见的数据结构——数组
3.队列
用计算机程序处理数据时,有时也需要将数据进行“排队”,并遵循现实中排队的规律,对数据进行“先进先出” FIFO(First In First Out)且中间不能“插队”的组织和操作,计算机科学家由此发明了“队列”这种数据结构。
常见的数据结构——数组
4.栈
弹匣的装弹过程(入栈)
栈的示例—弹匣
子弹进出弹匣的过程具有下列特点:
①整个装置只有一端开放(最上端),而且进、出只能在这一端进行。
②弹匣中的子弹成一纵队排列。
③任何子弹进出弹匣的规律是“先进后出、后进先出”,即最先装入弹匣的子弹最后才能被弹出,而最后装入弹匣的子弹则最先被弹出。
常见的数据结构——数组
4.栈
栈的示例—弹匣
子弹是数据元素
弹匣是栈结构
子弹只从一个头即栈顶进出
装弹过程是Push入栈
开枪过程是Pop出栈
在这里,压与弹体现这两个字的真正含义
常见的数据结构——数组
4.栈
概 念:栈是一种先进后出的操作受限的线性表,仅允许在表的一端进行插入或删除。
栈 顶:进行插入或删除操作的一端。
栈顶元素:位于栈顶位置的元素。
栈 底:不进行操作的一端。
栈底元素:位于栈底位置的元素。
栈底元素
栈顶元素
问题与讨论?
问题与讨论?
问题与讨论?
队列的特点?
先进先出,不能插队
栈的特点?
先进后出,后进先出
队列和栈有什么共同点?
都是线性关系
常见的数据结构——数组
5.树
一个元素前面(或上面)只有一个元素,而后面(或下面)却有多个(0个或多个)元素相邻,所有的数据元素之间的特征就像一棵倒放的树。
常见的数据结构——数组
5.树
概念:树是由n(n≧0)个节点构成的一个有限集合以及在该集合上定义的一种节点关系。
节点:集合中的元素。
空树:n=0的树。
子树:树中某个节点下面的所有节点所构成的树。
第1层
第2层
第3层
第4层
常见的数据结构——数组
5.树
特殊的树——二叉树
概念:指树中节点的度不大于2的有序树
常见的数据结构——数组
6.图
概念:图(Graph)结构是一种非线性的数据结构,图在实际生活中有很多例子,比如交通运输网,地铁网络,社交网络,计算机中的状态执行(自动机)等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。
数据结构的作用
1.设计算法解决问题离不开数据结构
2.不同数据结构会导致处理效率的不同
03
数据结构的作用
1.设计算法解决问题离不开数据结构
数据统计前,需要先收集数据并将数据按照既有的逻辑关系进行结构化组织,可以用一张表格来组织数据并表示数据之间的逻辑关系。
例:某学校举行趣味运动会,高一开设了“滚铁圈”,“打弹子”,“拍纸板”“竹蜻蜓”、“跳绳”、“踢毽子”6个项目的比赛,比赛结束后需要根据每个选手各个项目的得分来统计每位选手的总分以及各班级的总分。
数据结构的作用
1.设计算法解决问题离不开数据结构
例:某学校举行趣味运动会,高一开设了“滚铁圈”,“打弹子”,“拍纸板”“竹蜻蜓”、“跳绳”、“踢毽子”6个项目的比赛,比赛结束后需要根据每个选手各个项目的得分来统计每位选手的总分以及各班级的总分。
数据结构的作用
2.不同数据结构会导致处理效率的不同
将这张表的数据存入计算机,可以用什么数据结构存储,为什么?
数据结构的作用
2.不同数据结构会导致处理效率的不同
方法一:用一维数组组织数据
其中的bjdf(j)表示第j班的总分
程序代码:
数据结构的作用
2.不同数据结构会导致处理效率的不同
方法二:用二维数组组织数据
程序代码:
其中的bjdf(j)表示第j班的总分
数据结构的作用
2.不同数据结构会导致处理效率的不同
二维数组程序实现:
一维数组程序实现:
2.不同数据结构会导致处理效率的不同
数据合并案例:
生产厂家总会根据各地产品销量的数据分析来预估市场情况,并为后续调整生产规划、完善营销策略提供依据。
由于数据量巨大,为了充分运用分布式处理的优势,总部会要求各下属地区上报数据时,按各产品销量进行从大到小的排序。总部收到数据后的第一件事是将所有数据合并并按照销量进行降序排序(从大到小),为了完成数据合并和整理工作,总部数据分析员小刚需要设计合适的数据结构和算法。
分析
小刚可以用一个二维数组存储所有下属地区的产品销量数据,然后直接运用排序算法进行降序排序。如果利用既有数据已是分块有序的特点,设计新的数据结构和算法,则处理效率可以得到相应的提升。
各个地区的数据合并问题可以简化为2个地区的数据合并问题,当2个地区的数据合并完成后,剩余各地区的数据合并就可以按照同样方式完成。因此,接下来着重分析2个地区的数据合并问题。
2.不同数据结构会导致处理效率的不同
第一步 抽象与建模
设第1个地区共有n个产品销量数据,第2个地区共有m个产品销量数据。为了简化描述,突出核心部分的分析,考虑将问题抽象为n个有序整数和m个有序整数的合并问题,具体的问题模型如下:
已知一个降序排列的整数数列A :a1,a2,a3,…,an以及一个降序排列的整数数列B:b1,b2,b 3,…,bm ,将两个数列合并形成一个新的有序数列C,使新数列仍按降序排列,即c1≥c2≥c3≥…≥ck≥ck+1≥…≥cn+m(其中ck ∈A或者ck ∈B)。请完成解决该问题的数据结构和算法的设计。
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(1)将数组a中所有元素存储到数组c的前n个位置中;
a
19
16
12
8
5
b
20
15
14
10
4
c
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(2)将数组c右边的m个元素赋值为–1(c(n+1)直到c(n+m));
a
19
16
12
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
-1
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(3)变量p赋值为0,将表示数组c中有效元素总个数的变量tot赋值为n ;
a
19
16
12
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
-1
0
i
p
tot
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
19
16
12
-1
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
0
i
p
tot
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
-1
5
19
16
12
8
b
20
15
14
10
4
c
-1
-1
-1
0
i
p
tot
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
②如果c(p)>b(i),那么使p值增加1;
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
19
16
12
8
5
-1
b
20
15
14
10
4
c
0
i
tot
p
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
2. 基于链表的算法设计与描述
链表a:
head_a
指针p1
指针p
链表b:
head_b
指针q1
指针q
小结
2、不同数据结构会导致处理效率的不同
·数组的优点
(1)随机访问性强
(2)查找速度快
·数组的缺点
(1)插入和删除效率低
(2)可能浪费内存
(3)内存空间要求高,必须有充足
的连续内存空间
(4)数组大小固定,不能动态拓展
·链表的优点
(1)插入删除速度快
(2)内存利用率高,不会浪费内存
(3)大小没有固定,拓展灵活
·链表的缺点
不能随意查找,必须从第一个开始遍历,查找效率低
CHZX
1.2 数据的组织
浙江省高中信息技术 选择性必修一 《数据与数据结构》
数据结构的概念
数据元素
数据类型
数据结构
01
1.数据元素
数据元素是数据的基本单位。有些情况下,数据元素也称为元素、结点、顶点、记录等。
有时一个数据元素可以由若干个数据项(也称字段、域)组成,数据项是具有独立含义的最小数据表示单位。
1.2.1数据结构的概念
数据项
数据元素
数据元素
1.数据元素
Q1:这张表一共有多少个数据元素?
1.2.1数据结构的概念
10个
Q2:第三个数据元素的第三个数据项的名称为什么?值为什么?
最新价格(元/股)9.92
2.数据类型
数据类型指的是具有相同性质的计算机数据的集合及在这个数据集合上的一组操作。数据类型可以分为基本数据类型(也称为原子数据类型)和结构数据类型。
1.2.1数据结构的概念
基本数据类型由计算机编程环境提供,编程者可以在编程时直接用系统提供的标识符进行定义,如Python编程语言中的整型、实型、布尔型等。
结构数据类型是在程序设计时利用基本数据类型构造出的、复合的新类型,这种新类型由用户根据实际需要定义,能较好地描述数据元素数据项组成以及数据元素之间的逻辑关系,方便用户根据数据之间逻辑关系的特点进行数据处理,如很多编程语言中提供的记录类型、集合等。
基本数据类型
结构数据类型
3.数据结构
数据结构指的是数据之间的相互关系,即数据的组织形式。它包括了以下三个方面的内容:
①数据元素之间的逻辑关系,也称为数据的逻辑结构。
②数据元素及其关系在计算机存储器内的表示,也称为数据的存储结构或物理结构。
③数据的运算,即对数据施加的操作。
1.2.1数据结构的概念
课堂练习
B
B
常见的数据结构
数组
链表
队列
栈
树
02
现实中表示一批数据,有时不仅需要描述数据对象本身,还需要描述数据所处的位置或者数据之间的前后顺序关系,便可以用数组这种数据结构来实现(存储的都是同种数据类型)
排队:
常见的数据结构——数组
这批数据序列可用数组a
1.数组
所处位置
(下标)
数据本身
(元素)
1 2 3 4
李彤 张强 胡洁 杜刚
a[1]="李彤"
a[2]="张强"
a[3]="胡洁"
a[4]="杜刚"
常见的数据结构——数组
1.数组
也可以通过变量名后面的下标依次按顺序遍历序列中的每个元素。
例:用sg数组来存放身高信息,sg=[165,169,185,179,172,191]
sg[0]=165(下标从0开始)
用数组组织数据时,可以快速通过下标精准地访问序列中的某个元素
方法一:
sg=[165,169,185,179,172,191]
for i in range(6):
print(sg[i])
方法二:
sg=[165,169,185,179,172,191]
for i in sg:
print(i)
常见的数据结构——数组
1.数组
例:sname = [‘a’, ’b’, ’c’, ’d’, ’e’]
在python语言中没有数组这种数据结构,但是列表可以完成数组的功能。
元素
顺序索引
逆序索引
访问元素“b”?
在元素“c”和元素“d”中间插入元素“x”?
问题一:现实生活中,有哪些数据适合用数组来存储?
问题与讨论?
特点:同种数据类型
超市商品的价格
统计全班同学的生日
杭州到全国各省会城市的机票价格
……
问题二:排队时,你是如何记住自己的位置的?
常见的数据结构——数组
2.链表
吴坚知道自己排在首位,王林知道排在自己前面的是吴坚,黄刚知道排在自己前面的是王林,李丰知道排在自己前面的是黄刚。有了这些相邻人员之间的链接关系,即使休息时大家分散在各处,一旦需要集合,大家可以根据链接关系快速地按照原顺序排成队伍。虽然整队前后每个人员的站位地点发生改变,但相互之间排队的顺序关系是不变的。
常见的数据结构——数组
2.链表
抽象化后的排队链接关系
组织、处理一批数据时,若不关心数据实际所处的具体位置,而只需知道数据之间相互链接的顺序时,可以借鉴上面的方法。在计算机科学中,这种方法的具体实现形式就是链表。
常见的数据结构——数组
2.链表
单向链表
头节点,便可以从head指向的头节点开始依次遍历链表中的每个节点
思考:该链表的指针指向的是前面还是后面?
常见的数据结构——数组
2.链表
链表内存存放方式:
head
(头节点)
tail
None
数据域
指针域
My_list
基本元素:
(1)节点:每个节点有两个部分,左边称为数值域,存放用户数据;右边部分称为指针域,用来存放指向下一个元素的指针(地址)。
(2)head:head节点永远指向第一个节点
(3)tail:tail永远指向最后一个节点
(4)None:链表中最后一个节点的指针域为None值
常见的数据结构——数组
2.链表
单向链表
双向链表
单链表的基础上,增加一个指向前趋节点的链接
基于单向链表的循环链表
单链表的基础上,在链表的首尾之间增加链接
问题与讨论?
何为单向链表、双向链表、基于单向链表的循环链表?
单向链表
双向链表
基于单向链表的循环链表
问题与讨论?
数组的特点?
不仅需要描述数据对象本身,还需要描述数据所处的位置或者数据之间的前后顺序关系
链表的特点?
只需知道数据之间相互链接的顺序
在数组中插入元素和在链表中插入元素的差别?
数组:整体后移空出位置插入
链表:改变指针
常见的数据结构——数组
3.队列
有序排队上车的乘客
有序排队接客的出租车
乘客排队时先到的总是从队伍的头部出去(出队)上车,而后到的乘客则必须在队伍的尾部加入(入队)。同时,为了确保有序,人们总是规定不能从队伍的中间部位插队。
常见的数据结构——数组
3.队列
概 念:队列是一种先进先出的线性表,允许插入的一端称为队尾,允许删除的一端称为队首
队列元素:队列中的数据元素。
入 队:在队列中插入一个元素的过程。
出 队:从队列中删除一个元素的过程。
出队
入队
队首元素
队尾元素
常见的数据结构——数组
3.队列
用计算机程序处理数据时,有时也需要将数据进行“排队”,并遵循现实中排队的规律,对数据进行“先进先出” FIFO(First In First Out)且中间不能“插队”的组织和操作,计算机科学家由此发明了“队列”这种数据结构。
常见的数据结构——数组
4.栈
弹匣的装弹过程(入栈)
栈的示例—弹匣
子弹进出弹匣的过程具有下列特点:
①整个装置只有一端开放(最上端),而且进、出只能在这一端进行。
②弹匣中的子弹成一纵队排列。
③任何子弹进出弹匣的规律是“先进后出、后进先出”,即最先装入弹匣的子弹最后才能被弹出,而最后装入弹匣的子弹则最先被弹出。
常见的数据结构——数组
4.栈
栈的示例—弹匣
子弹是数据元素
弹匣是栈结构
子弹只从一个头即栈顶进出
装弹过程是Push入栈
开枪过程是Pop出栈
在这里,压与弹体现这两个字的真正含义
常见的数据结构——数组
4.栈
概 念:栈是一种先进后出的操作受限的线性表,仅允许在表的一端进行插入或删除。
栈 顶:进行插入或删除操作的一端。
栈顶元素:位于栈顶位置的元素。
栈 底:不进行操作的一端。
栈底元素:位于栈底位置的元素。
栈底元素
栈顶元素
问题与讨论?
问题与讨论?
问题与讨论?
队列的特点?
先进先出,不能插队
栈的特点?
先进后出,后进先出
队列和栈有什么共同点?
都是线性关系
常见的数据结构——数组
5.树
一个元素前面(或上面)只有一个元素,而后面(或下面)却有多个(0个或多个)元素相邻,所有的数据元素之间的特征就像一棵倒放的树。
常见的数据结构——数组
5.树
概念:树是由n(n≧0)个节点构成的一个有限集合以及在该集合上定义的一种节点关系。
节点:集合中的元素。
空树:n=0的树。
子树:树中某个节点下面的所有节点所构成的树。
第1层
第2层
第3层
第4层
常见的数据结构——数组
5.树
特殊的树——二叉树
概念:指树中节点的度不大于2的有序树
常见的数据结构——数组
6.图
概念:图(Graph)结构是一种非线性的数据结构,图在实际生活中有很多例子,比如交通运输网,地铁网络,社交网络,计算机中的状态执行(自动机)等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。
数据结构的作用
1.设计算法解决问题离不开数据结构
2.不同数据结构会导致处理效率的不同
03
数据结构的作用
1.设计算法解决问题离不开数据结构
数据统计前,需要先收集数据并将数据按照既有的逻辑关系进行结构化组织,可以用一张表格来组织数据并表示数据之间的逻辑关系。
例:某学校举行趣味运动会,高一开设了“滚铁圈”,“打弹子”,“拍纸板”“竹蜻蜓”、“跳绳”、“踢毽子”6个项目的比赛,比赛结束后需要根据每个选手各个项目的得分来统计每位选手的总分以及各班级的总分。
数据结构的作用
1.设计算法解决问题离不开数据结构
例:某学校举行趣味运动会,高一开设了“滚铁圈”,“打弹子”,“拍纸板”“竹蜻蜓”、“跳绳”、“踢毽子”6个项目的比赛,比赛结束后需要根据每个选手各个项目的得分来统计每位选手的总分以及各班级的总分。
数据结构的作用
2.不同数据结构会导致处理效率的不同
将这张表的数据存入计算机,可以用什么数据结构存储,为什么?
数据结构的作用
2.不同数据结构会导致处理效率的不同
方法一:用一维数组组织数据
其中的bjdf(j)表示第j班的总分
程序代码:
数据结构的作用
2.不同数据结构会导致处理效率的不同
方法二:用二维数组组织数据
程序代码:
其中的bjdf(j)表示第j班的总分
数据结构的作用
2.不同数据结构会导致处理效率的不同
二维数组程序实现:
一维数组程序实现:
2.不同数据结构会导致处理效率的不同
数据合并案例:
生产厂家总会根据各地产品销量的数据分析来预估市场情况,并为后续调整生产规划、完善营销策略提供依据。
由于数据量巨大,为了充分运用分布式处理的优势,总部会要求各下属地区上报数据时,按各产品销量进行从大到小的排序。总部收到数据后的第一件事是将所有数据合并并按照销量进行降序排序(从大到小),为了完成数据合并和整理工作,总部数据分析员小刚需要设计合适的数据结构和算法。
分析
小刚可以用一个二维数组存储所有下属地区的产品销量数据,然后直接运用排序算法进行降序排序。如果利用既有数据已是分块有序的特点,设计新的数据结构和算法,则处理效率可以得到相应的提升。
各个地区的数据合并问题可以简化为2个地区的数据合并问题,当2个地区的数据合并完成后,剩余各地区的数据合并就可以按照同样方式完成。因此,接下来着重分析2个地区的数据合并问题。
2.不同数据结构会导致处理效率的不同
第一步 抽象与建模
设第1个地区共有n个产品销量数据,第2个地区共有m个产品销量数据。为了简化描述,突出核心部分的分析,考虑将问题抽象为n个有序整数和m个有序整数的合并问题,具体的问题模型如下:
已知一个降序排列的整数数列A :a1,a2,a3,…,an以及一个降序排列的整数数列B:b1,b2,b 3,…,bm ,将两个数列合并形成一个新的有序数列C,使新数列仍按降序排列,即c1≥c2≥c3≥…≥ck≥ck+1≥…≥cn+m(其中ck ∈A或者ck ∈B)。请完成解决该问题的数据结构和算法的设计。
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(1)将数组a中所有元素存储到数组c的前n个位置中;
a
19
16
12
8
5
b
20
15
14
10
4
c
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(2)将数组c右边的m个元素赋值为–1(c(n+1)直到c(n+m));
a
19
16
12
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
-1
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
1. 基于数组的算法设计与描述
(3)变量p赋值为0,将表示数组c中有效元素总个数的变量tot赋值为n ;
a
19
16
12
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
-1
0
i
p
tot
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
19
16
12
-1
8
5
b
20
15
14
10
4
c
-1
-1
-1
-1
0
i
p
tot
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
-1
5
19
16
12
8
b
20
15
14
10
4
c
-1
-1
-1
0
i
p
tot
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
②如果c(p)>b(i),那么使p值增加1;
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
(4)将数组b中元素b(i)逐个插入到数组c中(1≤i≤m):
①p值增加1;
②如果c(p)>b(i),那么使p值增加1;
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
④ 如果c(p)≤b(i),那么依次将c(tot),c(tot–1),…,c(p)向右移动一个位置,然后将b(i)存储到c(p)中,同时tot值增加1。
19
16
12
8
5
-1
b
20
15
14
10
4
c
0
i
tot
p
③如果c(p)=–1,那么直接将b(i)存储到c(p)中,同时tot值增加1;
2.不同数据结构会导致处理效率的不同
第二步 设计、描述算法
2. 基于链表的算法设计与描述
链表a:
head_a
指针p1
指针p
链表b:
head_b
指针q1
指针q
小结
2、不同数据结构会导致处理效率的不同
·数组的优点
(1)随机访问性强
(2)查找速度快
·数组的缺点
(1)插入和删除效率低
(2)可能浪费内存
(3)内存空间要求高,必须有充足
的连续内存空间
(4)数组大小固定,不能动态拓展
·链表的优点
(1)插入删除速度快
(2)内存利用率高,不会浪费内存
(3)大小没有固定,拓展灵活
·链表的缺点
不能随意查找,必须从第一个开始遍历,查找效率低
