人教版八年级下册 18.1.1 平行四边形的性质 同步课堂小测(含答案)
文档属性
| 名称 | 人教版八年级下册 18.1.1 平行四边形的性质 同步课堂小测(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 00:00:00 | ||
图片预览


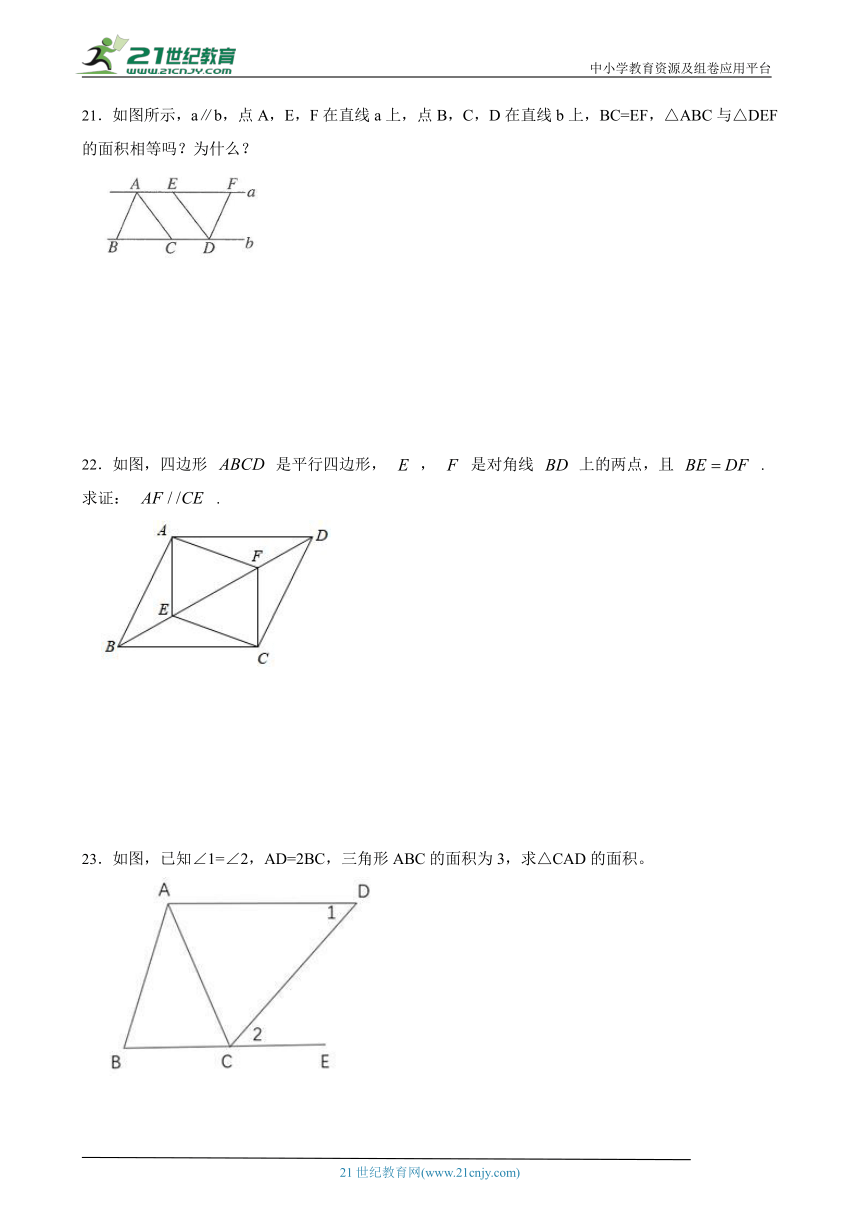
文档简介
中小学教育资源及组卷应用平台
人教版八年级下册18.1.1平行四边形的性质小测
一、单选题
1.在平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=40°,∠CBD=25°,则∠COD等于( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.60° B.65° C.70° D.75°
2.下列说法:①伸缩门的制作运用了四边形的 ( http: / / www.21cnjy.com )不稳定性;②夹在两条平行线间的垂线段相等;③成中心对称的两个图形不一定是全等形;④一组对角相等的四边形是平行四边形,其中正确的有几个?( ) 2·1·c·n·j·y
A.1个 B.2个 C.3个 D.4个
3.在 ABCD中,∠A:∠B=7:2,则∠C的度数是( )
A.40° B.70° C.105° D.140°
4.如图,点P为 ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.10 B.13 C.18 D.20
5.如图,在¨ABCD中,∠A=110°,BE平分∠ABC交边AD于点E,则∠BED的度数为( )
( http: / / www.21cnjy.com / )
A.135° B.140° C.145° D.150°
6.已知平行四边形邻边之比是1:2,周长是18,则较短的边的边长是( )
A.3 B.6 C.9 D.12
7.已知在□ABCD中,∠B+∠D=200°,则∠B的度数为( )
A.100° B.160° C.80° D.60°
8.如图,在□ABCD 中,∠ABD=25 ( http: / / www.21cnjy.com )°,现将□ABCD 沿 EF 折叠,使点 B 与点 D 重合,点 C 落在点 G 处, 若 G 在 AD 延长线上,则∠GDF 的度数是( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A.45° B.50° C.60° D.65°
9.如图,在平行四边形ABCD中,,,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
10.平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对边相等
二、填空题
11.已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O,点A(-1,3),则点C的坐标为 .21*cnjy*com
12.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AE交BC于点E,若BF=8,EB=6,则AE的长为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
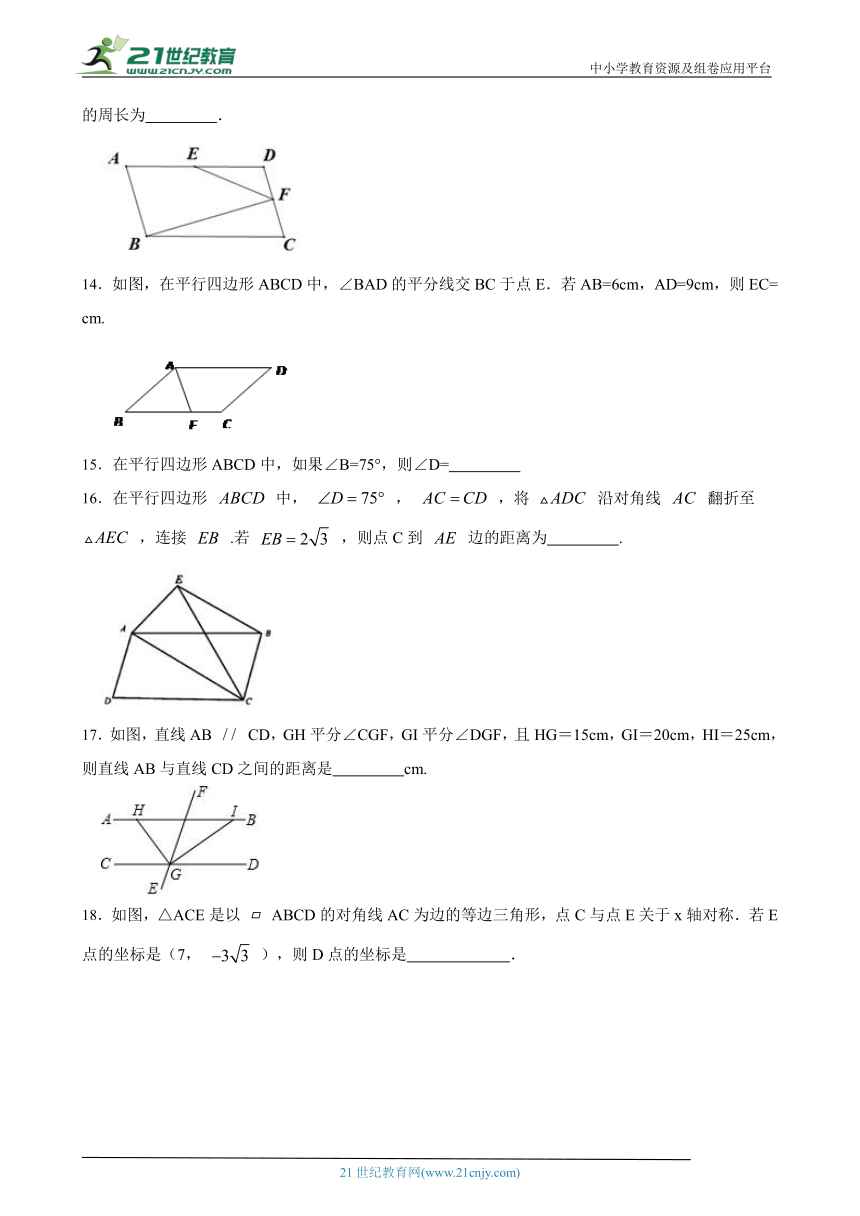
13.如图,在 ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则 ABCD的周长为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
14.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E.若AB=6cm,AD=9cm,则EC= cm.【版权所有:21教育】
( http: / / www.21cnjy.com / )
15.在平行四边形ABCD中,如果∠B=75°,则∠D=
16.在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为 .
( http: / / www.21cnjy.com / )
17.如图,直线AB CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是 cm. 21教育名师原创作品
( http: / / www.21cnjy.com / )
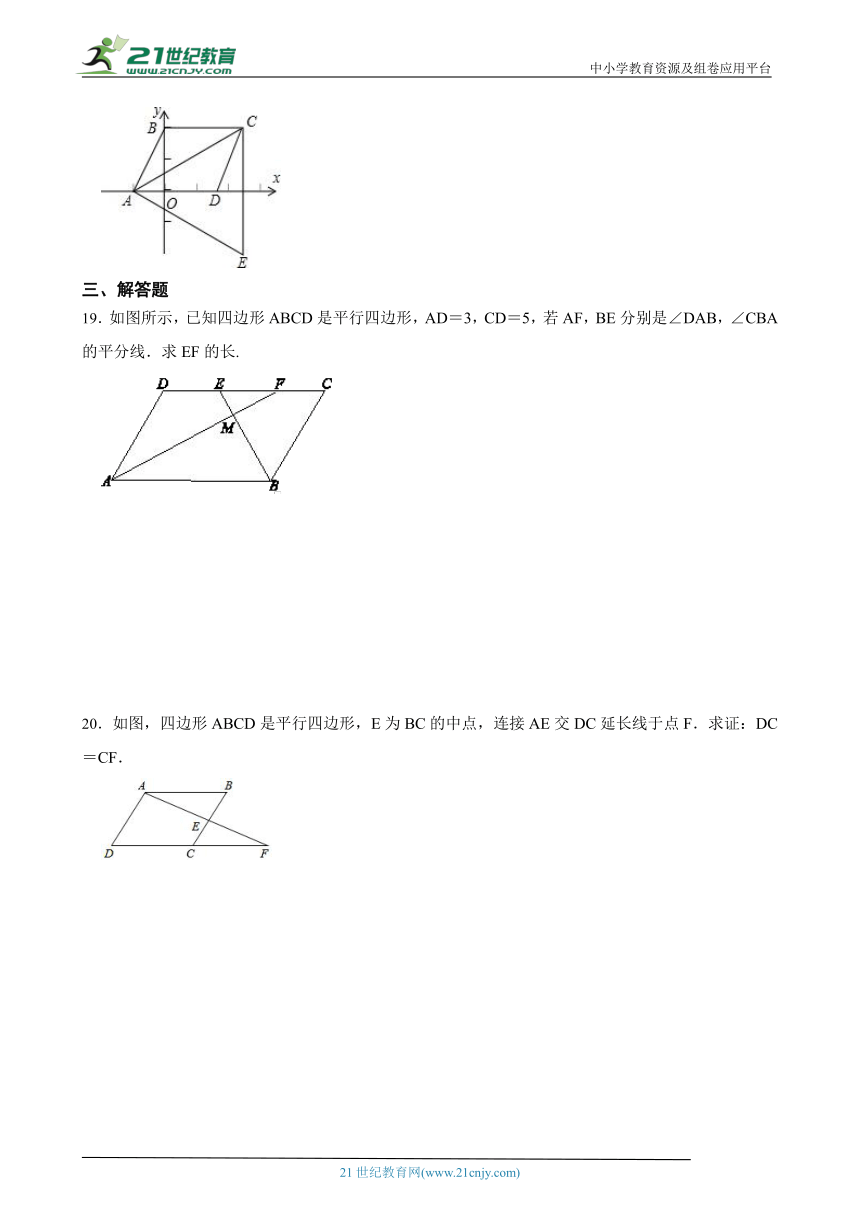
18.如图,△ACE是以 ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7, ),则D点的坐标是 . 21*cnjy*com
( http: / / www.21cnjy.com / )
三、解答题
19.如图所示,已知四边形ABCD是平行四边形,AD=3,CD=5,若AF,BE分别是∠DAB,∠CBA的平分线.求EF的长.
( http: / / www.21cnjy.com / )
20.如图,四边形ABCD是平行四边形,E为BC的中点,连接AE交DC延长线于点F.求证:DC=CF.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
21.如图所示,a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF,△ABC与△DEF的面积相等吗?为什么?21·世纪*教育网
( http: / / www.21cnjy.com / )
22.如图,四边形 是平行四边形, , 是对角线 上的两点,且 .求证: . 21世纪教育网版权所有
( http: / / www.21cnjy.com / )
23.如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求△CAD的面积。
( http: / / www.21cnjy.com / )
24.为了确保学生上下学期间的交通安全,某校在校门口附近的十字路口派值班老师负责指挥学生横过公路.如图,四位值班老师是平行四边形站位(在的四个顶点的位置),立在路上的交通指示灯在AC、BD交点O处,且知,站在A、B两点处的两位老师的距离为10米,站在B、C两点处的两位老师的距离为8米,求站在B、D两点处的两位老师的距离.
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】A
11.【答案】(1,-3)
12.【答案】
13.【答案】
14.【答案】3
15.【答案】75°
16.【答案】
17.【答案】12
18.【答案】(5,0)
19.【答案】解:∵平行四边形ABCD
∴AB // CD,AD = BC
∵ AF ,BE分别是∠DAB,∠CBA的平分线
20.【答案】证明:∵四边形ABCD是平行四边形,
∴,,
∴.
∵E为BC的中点,
∴.
在和中,
,
∴,
∴,
∴.
21.【答案】解:△ABC和△DEF的面积相等。理由如下:
( http: / / www.21cnjy.com / )
如图,过点A作AH1⊥直线b,垂足为点H1,过点D作DH2⊥直线a,垂足为点H2,设△ABC和△DEF的面积分别为S1和S2,21教育网
则S1=BCAH1,S2=EF·DH2
∵a∥b,AH1⊥直线b,DH2⊥直线a,
AHI=DH2
又∵BC=EF,
S1=S2,即△ABC与△DEF的面积相等。
22.【答案】解: 四边形 是平行四边形,
, , , ,
,
∵BE=DF,
∴BE+EF=EF+DF,
即BF=DE
在 和 中,
,
,
,
.
23.【答案】解:∵ ∠1=∠2,
∴ ( http: / / www.21cnjy.com )AD∥BC,
∴ △CAD和△ABC的高相等,
∵ AD=2BC,
∴S△CAD=2S△ABC=2×3=6.21cnjy.com
24.【答案】解:在Rt△ABC中,由勾股定理得:(米),
∵四边形ABCD是平行四边形
∴(米),
在Rt△OBC中,由勾股定理得:
∴(米)
答:站在B、D两点处的两位老师的距离是米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级下册18.1.1平行四边形的性质小测
一、单选题
1.在平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=40°,∠CBD=25°,则∠COD等于( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.60° B.65° C.70° D.75°
2.下列说法:①伸缩门的制作运用了四边形的 ( http: / / www.21cnjy.com )不稳定性;②夹在两条平行线间的垂线段相等;③成中心对称的两个图形不一定是全等形;④一组对角相等的四边形是平行四边形,其中正确的有几个?( ) 2·1·c·n·j·y
A.1个 B.2个 C.3个 D.4个
3.在 ABCD中,∠A:∠B=7:2,则∠C的度数是( )
A.40° B.70° C.105° D.140°
4.如图,点P为 ABCD外一点,连接PA、PB、PC、PD,若△APB的面积为18,△APD的面积为5,则△APC的面积为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.10 B.13 C.18 D.20
5.如图,在¨ABCD中,∠A=110°,BE平分∠ABC交边AD于点E,则∠BED的度数为( )
( http: / / www.21cnjy.com / )
A.135° B.140° C.145° D.150°
6.已知平行四边形邻边之比是1:2,周长是18,则较短的边的边长是( )
A.3 B.6 C.9 D.12
7.已知在□ABCD中,∠B+∠D=200°,则∠B的度数为( )
A.100° B.160° C.80° D.60°
8.如图,在□ABCD 中,∠ABD=25 ( http: / / www.21cnjy.com )°,现将□ABCD 沿 EF 折叠,使点 B 与点 D 重合,点 C 落在点 G 处, 若 G 在 AD 延长线上,则∠GDF 的度数是( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A.45° B.50° C.60° D.65°
9.如图,在平行四边形ABCD中,,,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
10.平行四边形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行 D.对边相等
二、填空题
11.已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O,点A(-1,3),则点C的坐标为 .21*cnjy*com
12.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AE交BC于点E,若BF=8,EB=6,则AE的长为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
13.如图,在 ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则 ABCD的周长为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
14.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E.若AB=6cm,AD=9cm,则EC= cm.【版权所有:21教育】
( http: / / www.21cnjy.com / )
15.在平行四边形ABCD中,如果∠B=75°,则∠D=
16.在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为 .
( http: / / www.21cnjy.com / )
17.如图,直线AB CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是 cm. 21教育名师原创作品
( http: / / www.21cnjy.com / )
18.如图,△ACE是以 ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7, ),则D点的坐标是 . 21*cnjy*com
( http: / / www.21cnjy.com / )
三、解答题
19.如图所示,已知四边形ABCD是平行四边形,AD=3,CD=5,若AF,BE分别是∠DAB,∠CBA的平分线.求EF的长.
( http: / / www.21cnjy.com / )
20.如图,四边形ABCD是平行四边形,E为BC的中点,连接AE交DC延长线于点F.求证:DC=CF.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
21.如图所示,a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF,△ABC与△DEF的面积相等吗?为什么?21·世纪*教育网
( http: / / www.21cnjy.com / )
22.如图,四边形 是平行四边形, , 是对角线 上的两点,且 .求证: . 21世纪教育网版权所有
( http: / / www.21cnjy.com / )
23.如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求△CAD的面积。
( http: / / www.21cnjy.com / )
24.为了确保学生上下学期间的交通安全,某校在校门口附近的十字路口派值班老师负责指挥学生横过公路.如图,四位值班老师是平行四边形站位(在的四个顶点的位置),立在路上的交通指示灯在AC、BD交点O处,且知,站在A、B两点处的两位老师的距离为10米,站在B、C两点处的两位老师的距离为8米,求站在B、D两点处的两位老师的距离.
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】A
10.【答案】A
11.【答案】(1,-3)
12.【答案】
13.【答案】
14.【答案】3
15.【答案】75°
16.【答案】
17.【答案】12
18.【答案】(5,0)
19.【答案】解:∵平行四边形ABCD
∴AB // CD,AD = BC
∵ AF ,BE分别是∠DAB,∠CBA的平分线
20.【答案】证明:∵四边形ABCD是平行四边形,
∴,,
∴.
∵E为BC的中点,
∴.
在和中,
,
∴,
∴,
∴.
21.【答案】解:△ABC和△DEF的面积相等。理由如下:
( http: / / www.21cnjy.com / )
如图,过点A作AH1⊥直线b,垂足为点H1,过点D作DH2⊥直线a,垂足为点H2,设△ABC和△DEF的面积分别为S1和S2,21教育网
则S1=BCAH1,S2=EF·DH2
∵a∥b,AH1⊥直线b,DH2⊥直线a,
AHI=DH2
又∵BC=EF,
S1=S2,即△ABC与△DEF的面积相等。
22.【答案】解: 四边形 是平行四边形,
, , , ,
,
∵BE=DF,
∴BE+EF=EF+DF,
即BF=DE
在 和 中,
,
,
,
.
23.【答案】解:∵ ∠1=∠2,
∴ ( http: / / www.21cnjy.com )AD∥BC,
∴ △CAD和△ABC的高相等,
∵ AD=2BC,
∴S△CAD=2S△ABC=2×3=6.21cnjy.com
24.【答案】解:在Rt△ABC中,由勾股定理得:(米),
∵四边形ABCD是平行四边形
∴(米),
在Rt△OBC中,由勾股定理得:
∴(米)
答:站在B、D两点处的两位老师的距离是米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
