人教版数学八年级下册 17.2 勾股定理的逆定理 同步课堂小测(含答案)
文档属性
| 名称 | 人教版数学八年级下册 17.2 勾股定理的逆定理 同步课堂小测(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 23:10:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册17.2勾股定理的逆定理小测
一、单选题
1.有4条线段,分别为 , , , ,从中任取3条,能构成直角三角形的概率是( ). 21cnjy.com
A. B. C. D.
2.已知 三边为 ,满足 ,则 是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形以
C.以c为斜边的直角三角形 D.不是直角三角形
3.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为3:4:5 B.三边长的平方之比为1:2:3
C.三边长之比为7:24:25 D.三内角之比为1:2:3
4.下列语句不能判定 是直角三角形的是( )
A. B.
C. D.
5.在下列条件:①∠A+∠B=∠C, ( http: / / www.21cnjy.com )②∠A:∠B:∠C=3:4:5,③∠C=∠A﹣∠B,④a:b:c=3:4:5中,能确定△ABC是直角三角形的条件有( ) 21教育网
A.1个 B.2个 C.3个 D.4个
6.一个三角形的两条边长分别是方程x2﹣8x+15=0的两根,三角形的周长是12,则该三角形的面积是( ) 21·cn·jy·com
A.5 B.6 C.7.5 D.12
7.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为 尺,则可列方程为( )
A. B.
C. D.
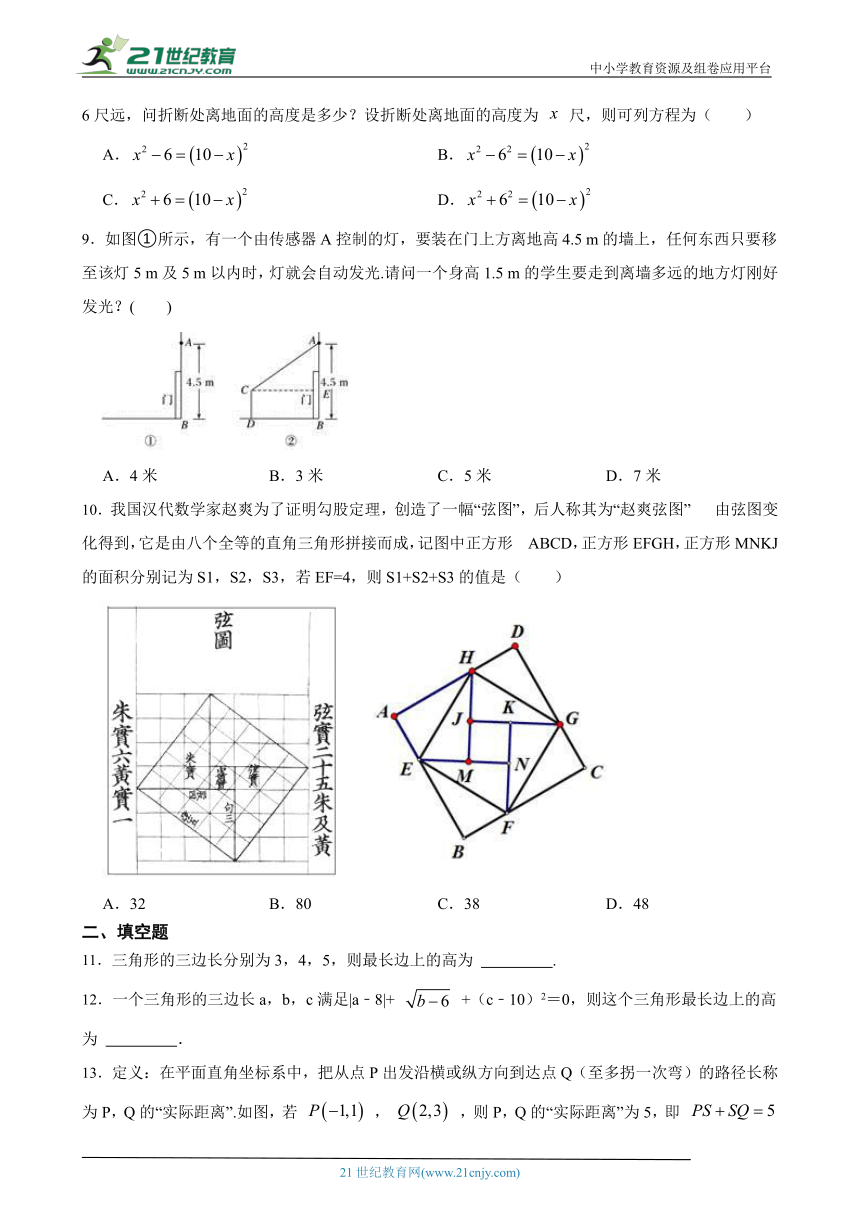
9.如图①所示,有一个由传感 ( http: / / www.21cnjy.com )器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光?( ) www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.4米 B.3米 C.5米 D.7米
10.我国汉代数学家赵爽为 ( http: / / www.21cnjy.com )了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图” 由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 ABCD,正方形EFGH,正方形MNKJ的面积分别记为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )21·世纪*教育网
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
A.32 B.80 C.38 D.48
二、填空题
11.三角形的三边长分别为3,4,5,则最长边上的高为 .
12.一个三角形的三边长a,b,c满足|a﹣8|+ +(c﹣10)2=0,则这个三角形最长边上的高为 . www-2-1-cnjy-com
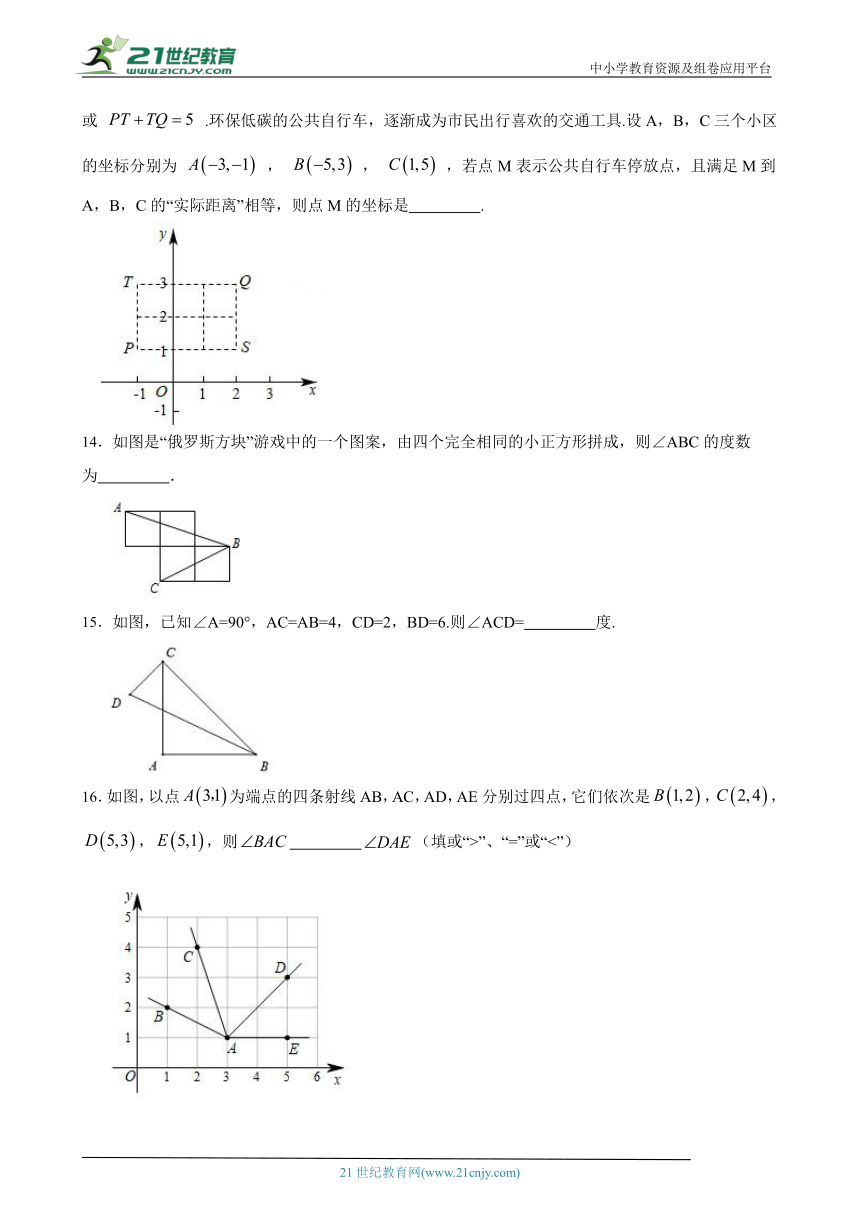
13.定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
14.如图是“俄罗斯方块”游戏中的一个图案,由四个完全相同的小正方形拼成,则∠ABC的度数为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
15.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
( http: / / www.21cnjy.com / )
16.如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则 (填或“>”、“=”或“<”)【版权所有:21教育】
( http: / / www.21cnjy.com / )
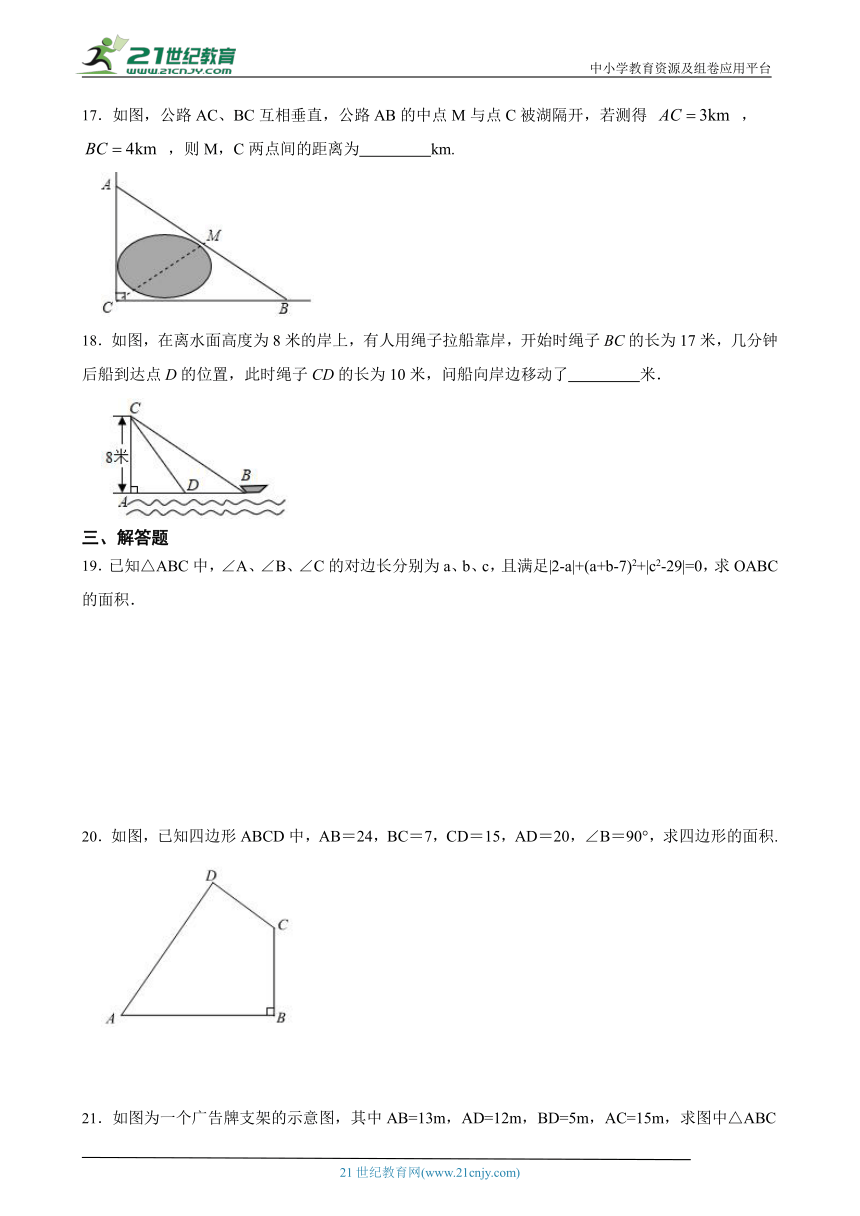
17.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为 km.21教育名师原创作品
( http: / / www.21cnjy.com / )
18.如图,在离水面高度为8米 ( http: / / www.21cnjy.com )的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
( http: / / www.21cnjy.com / )
三、解答题
19.已知△ABC中,∠A、∠B、∠C的对边长分别为a、b、c,且满足|2-a|+(a+b-7)2+|c2-29|=0,求OABC的面积.21*cnjy*com
20.如图,已知四边形ABCD中,AB=24,BC=7,CD=15,AD=20,∠B=90°,求四边形的面积.
( http: / / www.21cnjy.com / )
21.如图为一个广告牌支架的示意图,其中AB=13m,AD=12m,BD=5m,AC=15m,求图中△ABC面积.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
22.如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积.
( http: / / www.21cnjy.com / )
23.如图,某住宅社区在相邻两楼之 ( http: / / www.21cnjy.com )间修建一个上方是以AB为直径的半圆,下方是长方形的仿古通道,已知AD=2.3米,CD=2米;现有一辆卡车装满家具后,高2.5米,宽1.6米,请问这辆送家具的卡车能否通过这个通道?请说出你的理由.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
24.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 m,求点B到地面的垂直距离BC. 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】D
11.【答案】2.4
12.【答案】4.8
13.【答案】
14.【答案】45°
15.【答案】45
16.【答案】=
17.【答案】2.5
18.【答案】9
19.【答案】解:由题意,得2-a=0,a+b-7=0,c2-29=0,
解得a=2,b=5,c'=29,
∵22+52=29,即a2+b2=c2
∴△ABC是直角三角形,且∠C=90°.
∴△ABC的面积= ab= ×2×5=5.
20.【答案】解:如图,
( http: / / www.21cnjy.com / )
∵AB=24,BC=7,∠B=90°,
由勾股定理得AC2=242+72=625.
又∵CD=15,AD=20,
∴CD2十AD2=152+202=625,
∴AC2=CD2+AD2,
∴∠D=90°,
∴四边形ABCD的面积= ×24×7+ ×15×20=234.
21.【答案】解:∵AB=13m,AD=12m,BD=5m
∴
∴△ABD为直角三角形且
∴
∴△ADC为直角三角形
∴
∴
∴
∵
∴ m2.
22.【答案】解:∵ 在Rt△ABD中,∠A=90°,
∴ BD2=AB2+AD2=42+32=52,
∴ 在△CBD中,BD2+BC2=52+122=132,
∴ BD2+BC2=CD2,
∴ △CBD为直角三角形.
∴ S△ABD= AB·AD= ×4×3=6,
S△CBD= BC·BD= ×12×5=30,
∴ 四边形ABCD的面积=S△ABD+S△CBD=6+30=36
23.【答案】解:∵车宽1.6米,
∴卡车能否通过,只要比较距厂门中线0.8米处的高度与车高.
在Rt△OEF中,
( http: / / www.21cnjy.com / )
由勾股定理可得:
(m),
EH=EF+FH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
24.【答案】解:在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,AE=DE=3 .
∴AD2=AE2+DE2=(3 )2+(3 )2=36,
∴AD=6,即梯子的总长为6米.
∴AB=AD=6.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC= ,
AB=3,
∴BC2=AB2-AC2=62-32=27,
∴BC= m,
∴点B到地面的垂直距离BC=3 m.
在Rt△ADE中,运用勾股定理可求出梯子的总长度,在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.21世纪教育网版权所有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册17.2勾股定理的逆定理小测
一、单选题
1.有4条线段,分别为 , , , ,从中任取3条,能构成直角三角形的概率是( ). 21cnjy.com
A. B. C. D.
2.已知 三边为 ,满足 ,则 是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形以
C.以c为斜边的直角三角形 D.不是直角三角形
3.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为3:4:5 B.三边长的平方之比为1:2:3
C.三边长之比为7:24:25 D.三内角之比为1:2:3
4.下列语句不能判定 是直角三角形的是( )
A. B.
C. D.
5.在下列条件:①∠A+∠B=∠C, ( http: / / www.21cnjy.com )②∠A:∠B:∠C=3:4:5,③∠C=∠A﹣∠B,④a:b:c=3:4:5中,能确定△ABC是直角三角形的条件有( ) 21教育网
A.1个 B.2个 C.3个 D.4个
6.一个三角形的两条边长分别是方程x2﹣8x+15=0的两根,三角形的周长是12,则该三角形的面积是( ) 21·cn·jy·com
A.5 B.6 C.7.5 D.12
7.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为 尺,则可列方程为( )
A. B.
C. D.
9.如图①所示,有一个由传感 ( http: / / www.21cnjy.com )器A控制的灯,要装在门上方离地高4.5 m的墙上,任何东西只要移至该灯5 m及5 m以内时,灯就会自动发光.请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光?( ) www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.4米 B.3米 C.5米 D.7米
10.我国汉代数学家赵爽为 ( http: / / www.21cnjy.com )了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图” 由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形 ABCD,正方形EFGH,正方形MNKJ的面积分别记为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )21·世纪*教育网
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
A.32 B.80 C.38 D.48
二、填空题
11.三角形的三边长分别为3,4,5,则最长边上的高为 .
12.一个三角形的三边长a,b,c满足|a﹣8|+ +(c﹣10)2=0,则这个三角形最长边上的高为 . www-2-1-cnjy-com
13.定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
14.如图是“俄罗斯方块”游戏中的一个图案,由四个完全相同的小正方形拼成,则∠ABC的度数为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
15.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
( http: / / www.21cnjy.com / )
16.如图,以点为端点的四条射线AB,AC,AD,AE分别过四点,它们依次是,,,,则 (填或“>”、“=”或“<”)【版权所有:21教育】
( http: / / www.21cnjy.com / )
17.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为 km.21教育名师原创作品
( http: / / www.21cnjy.com / )
18.如图,在离水面高度为8米 ( http: / / www.21cnjy.com )的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了 米.
( http: / / www.21cnjy.com / )
三、解答题
19.已知△ABC中,∠A、∠B、∠C的对边长分别为a、b、c,且满足|2-a|+(a+b-7)2+|c2-29|=0,求OABC的面积.21*cnjy*com
20.如图,已知四边形ABCD中,AB=24,BC=7,CD=15,AD=20,∠B=90°,求四边形的面积.
( http: / / www.21cnjy.com / )
21.如图为一个广告牌支架的示意图,其中AB=13m,AD=12m,BD=5m,AC=15m,求图中△ABC面积.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
22.如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积.
( http: / / www.21cnjy.com / )
23.如图,某住宅社区在相邻两楼之 ( http: / / www.21cnjy.com )间修建一个上方是以AB为直径的半圆,下方是长方形的仿古通道,已知AD=2.3米,CD=2米;现有一辆卡车装满家具后,高2.5米,宽1.6米,请问这辆送家具的卡车能否通过这个通道?请说出你的理由.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
24.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 m,求点B到地面的垂直距离BC. 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】D
11.【答案】2.4
12.【答案】4.8
13.【答案】
14.【答案】45°
15.【答案】45
16.【答案】=
17.【答案】2.5
18.【答案】9
19.【答案】解:由题意,得2-a=0,a+b-7=0,c2-29=0,
解得a=2,b=5,c'=29,
∵22+52=29,即a2+b2=c2
∴△ABC是直角三角形,且∠C=90°.
∴△ABC的面积= ab= ×2×5=5.
20.【答案】解:如图,
( http: / / www.21cnjy.com / )
∵AB=24,BC=7,∠B=90°,
由勾股定理得AC2=242+72=625.
又∵CD=15,AD=20,
∴CD2十AD2=152+202=625,
∴AC2=CD2+AD2,
∴∠D=90°,
∴四边形ABCD的面积= ×24×7+ ×15×20=234.
21.【答案】解:∵AB=13m,AD=12m,BD=5m
∴
∴△ABD为直角三角形且
∴
∴△ADC为直角三角形
∴
∴
∴
∵
∴ m2.
22.【答案】解:∵ 在Rt△ABD中,∠A=90°,
∴ BD2=AB2+AD2=42+32=52,
∴ 在△CBD中,BD2+BC2=52+122=132,
∴ BD2+BC2=CD2,
∴ △CBD为直角三角形.
∴ S△ABD= AB·AD= ×4×3=6,
S△CBD= BC·BD= ×12×5=30,
∴ 四边形ABCD的面积=S△ABD+S△CBD=6+30=36
23.【答案】解:∵车宽1.6米,
∴卡车能否通过,只要比较距厂门中线0.8米处的高度与车高.
在Rt△OEF中,
( http: / / www.21cnjy.com / )
由勾股定理可得:
(m),
EH=EF+FH=0.6+2.3=2.9>2.5,
∴卡车能通过此门.
24.【答案】解:在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,AE=DE=3 .
∴AD2=AE2+DE2=(3 )2+(3 )2=36,
∴AD=6,即梯子的总长为6米.
∴AB=AD=6.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC= ,
AB=3,
∴BC2=AB2-AC2=62-32=27,
∴BC= m,
∴点B到地面的垂直距离BC=3 m.
在Rt△ADE中,运用勾股定理可求出梯子的总长度,在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.21世纪教育网版权所有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
