人教版数学八年级下册 18.2.1 矩形 同步课堂小测(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.2.1 矩形 同步课堂小测(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 23:09:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册18.2.1矩形小测
一、单选题
1.如图所示,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
( http: / / www.21cnjy.com / )
A.AB//DC B.AC=BD C.AC⊥BD D.OA=OC
2.将7张如图1的两边长分别为a和b(,a与b都为正整数)的矩形纸片按图2的方式不重叠地放在矩形内,矩形中未被覆盖的部分用阴影表示,设左上角与右下角的阴影部分的面积相等.设.若,k为整数,则a可取的值的个数为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.0个 B.4个 C.5个 D.无数个
3.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到△ECF.若BC=1,则△ECF的周长为( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A. B. C. D.
4.一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )
A.y=x(15-x) B.y=x(30-x) C.y=x(30-2x) D.y=x(15+x)
5.一个四边形要成为矩形,需要的条件是( )
A.两个内角相等 B.三个内角相等
C.四个内角相等 D.两个外角为直角
6.如图,将一张长方形纸片 ( http: / / www.21cnjy.com )ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,那么∠ADB的度数是( )
( http: / / www.21cnjy.com / )
A.18° B.20° C.36° D.45°
7.在□ABCD中,AB=3, ( http: / / www.21cnjy.com )BC=4,当口ABCD的面积最大时,下列结论:①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.其中正确的有( )21cnjy.com
A.①②③ B.①②④ C.②③④ D.①③④
8.如图,在矩形ABCD中,AB=2 ( http: / / www.21cnjy.com ),BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点E,EF⊥BD于点F,则OE+EF的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B.2 C. D.2
9.如图,在矩形 中, , 相交于点O,若 的面积是3,则矩形 的面积是( ) 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( ) 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.1:3 B.2:3 C.1:2 D.1:4
二、填空题
11.如图,将矩形ABCD沿AC折叠,使点B落在点B'处,B'C交AD于点E,若∠1=25°,则∠2的度数为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
12.如图, AFDE的顶点F在矩形ABCD ( http: / / www.21cnjy.com )的边BC上,点F与点B、C不重合,若△AED的面积为4,则图中阴影部分两个三角形的面积和为 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
13.如图,在中,,,,点P是AB上的任意一点,作于点D,于点E,连接DE,则DE的最小值为 .21*cnjy*com
( http: / / www.21cnjy.com / )
14.有一架竖直靠在直角墙面 ( http: / / www.21cnjy.com )的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在墙面BA,BC上,梯子MN的长度始终保持不变,MN=2,老鼠E在MN的中点处,猫在D点处,它到墙面BA,BC的距离分别为2和1.在此滑动过程中,猫与老鼠的距离DE的最小值为 .【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
15.如图,∠MON=90°,矩形 ( http: / / www.21cnjy.com )ABCD的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,点A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=3.运动过程中点D到点O的最大距离是 .
( http: / / www.21cnjy.com / )
16.如图,长方形纸片AB ( http: / / www.21cnjy.com )CD中,AB=8cm,BC=17cm,点O在边BC上,且OB=10cm.将纸片沿过点O的直线折叠,若点B恰好落在边AD上的点F处,则AF的长为 cm.
( http: / / www.21cnjy.com / )
17.如图,在长方形ABCD中,AB=3,BC=2,E是BC中点,点F是线段AB上一个动点.
( http: / / www.21cnjy.com / )
(1)连接DF,则DF+EF的最小值为 ;
(2)以EF为斜边向斜上方作等腰Rt△EFG,点F从点B运动到点A的过程中,AG的最小值为 .
18.如图,矩形ABCD的边CD上有一点E, , ,垂足为F,将 绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:① ;②四边形EFBC是正方形;③ ;④ ,其中结论正确的为 .(填写序号即可)
( http: / / www.21cnjy.com / )
三、解答题
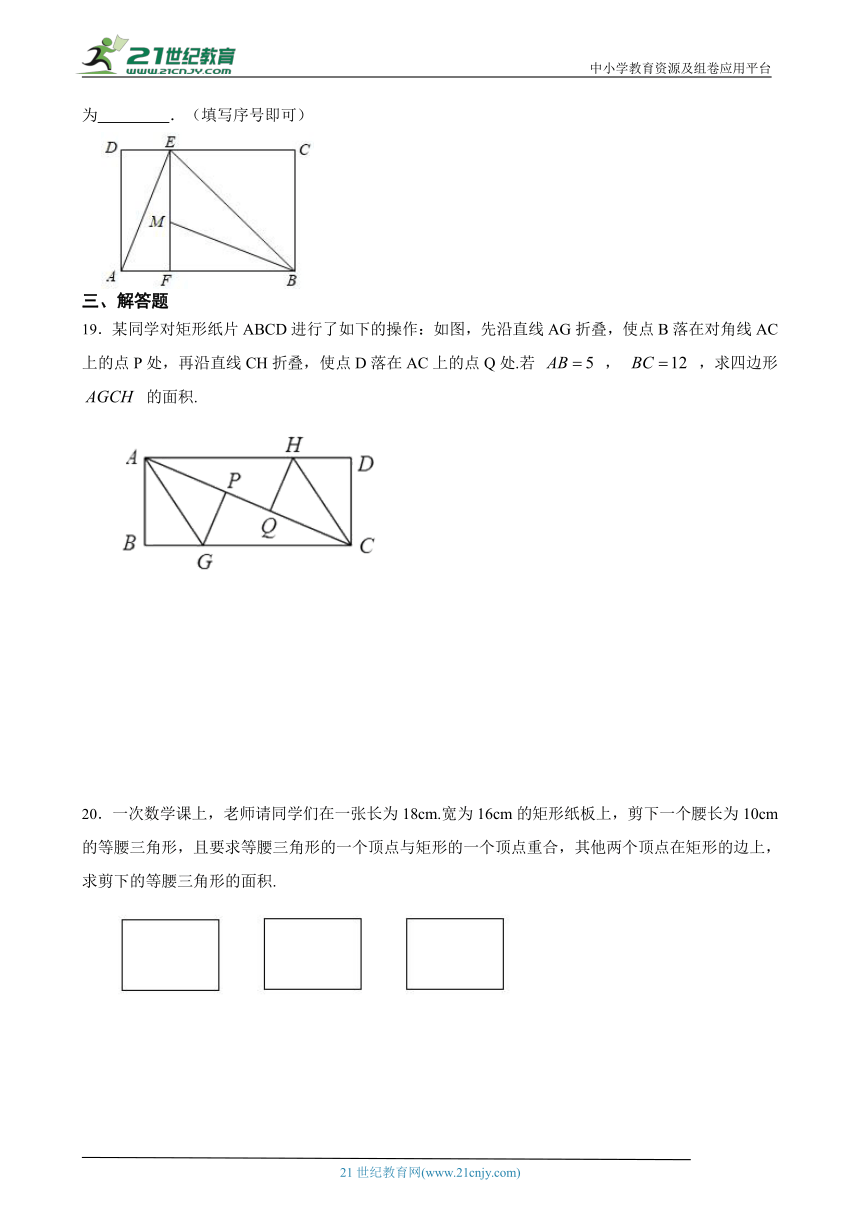
19.某同学对矩形纸片ABCD进行了如下的操作:如图,先沿直线AG折叠,使点B落在对角线AC上的点P处,再沿直线CH折叠,使点D落在AC上的点Q处.若 , ,求四边形 的面积. 21教育名师原创作品
( http: / / www.21cnjy.com / )
20.一次数学课上,老师请同学们在一 ( http: / / www.21cnjy.com )张长为18cm.宽为16cm的矩形纸板上,剪下一个腰长为10cm的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其他两个顶点在矩形的边上,求剪下的等腰三角形的面积.21·cn·jy·com
( http: / / www.21cnjy.com / )
21.如图,在四边形中,.点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使和,分别需经过多少时间?为什么?
( http: / / www.21cnjy.com / )
22.在Rt△ABC中,∠C=90°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.求证:四边形DEFC是矩形.21*cnjy*com
( http: / / www.21cnjy.com / )
23.如图,在矩形 中, ,且交 的延长线于点 .求证: .
( http: / / www.21cnjy.com / )
24.操作:第一步:如图1,对折长方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开.
( http: / / www.21cnjy.com / )
第二步:如图2,再一次折叠纸片 ( http: / / www.21cnjy.com ),使点A落在EF上的N处,并使折痕经过点B,得到折痕BM,同时得到线段BN.连结AN,易知△ABN的形状是 ▲ .2·1·c·n·j·y
论证:如图3,若延长MN交BC于点P,试判定△BMP的形状,请说明理由.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】50°
12.【答案】4
13.【答案】2.4
14.【答案】
15.【答案】
16.【答案】16
17.【答案】(1)
(2)
18.【答案】①②④
19.【答案】解:∵四边形ABCD是矩形, , ,
∴ , ,
∴ ,
由折叠的性质可知AP=AB=5,BG=PG,∠B=∠APG=90°,CQ=CD=5,
∴CP=8,∠CPG=90°,
设CG=x,则BG=PG=12-x,
∴由勾股定理可得: ,
解得: ,
即CG=,同理AH=,
∴CG=AH,
∵四边形ABCD是矩形,
∴AD∥BC,
∴四边形AGCH是平行四边形,21教育网
∴ .
20.【答案】解:分三种情况.
①如图1,在△AEF中,AE=AF=10cm,
( http: / / www.21cnjy.com / )
∴
②如图2,在△AGH中,AG=GH=10cm,
( http: / / www.21cnjy.com / )
∴BG=AB-AG=16-10=6(cm).
根据勾股定理,得BH=8cm,
∴
③如图3,在 中, ,
( http: / / www.21cnjy.com / )
∴ .
根据勾股定理,得DN=6cm,
∴
综上所述,剪下的等腰三角形的面积为50cm2或40cm2或30cm2.
21.【答案】解:①设经过,,
此时四边形成为平行四边形,
∵,
∴,
解得,
∴当s时,且PQ=CD
②设经过,,
如图所示,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F,当CF=EQ时,四边形PQCD为梯形(腰相等)或平行四边形,www.21-cn-jy.com
( http: / / www.21cnjy.com / )
∵,
∴四边形ABFD是矩形,
∴AD=BF,
∵AD=24cm,BC=26cm,
∴(cm),
当四边形PQCD为梯形(腰相等)时,,
∴,
解得,
∴当s时,PQ=CD,
当四边形为平行四边形或梯形(腰相等),为平行四边形时有s,PQ=CD,
综上所述,当s时,;当s或s时,PQ=CD.
22.【答案】证明:∵D,E,F分别是AC,AB,BC的中点,
∴DE∥FC,EF∥CD,
∴四边形DEFC是平行四边形,
∵∠DCF=90°,
∴四边形DEFC是矩形.
23.【答案】证明:∵四边形 是矩形,
∴ , .
∵
∴四边形 是平行四边形.
∴
24.【答案】解:等边三角形;论证:△BMP是等边三角形,理由如下:
如图3,∵△ABN是等边三角形,
∴∠ABN=60°,
∴∠NBM=∠ABM=∠ABN=30°,
∵∠NBP=∠ABP﹣∠ABN=30°,∠BNP=90°,
∴∠BPM=∠MBP=60°,
∴△BMP是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册18.2.1矩形小测
一、单选题
1.如图所示,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
( http: / / www.21cnjy.com / )
A.AB//DC B.AC=BD C.AC⊥BD D.OA=OC
2.将7张如图1的两边长分别为a和b(,a与b都为正整数)的矩形纸片按图2的方式不重叠地放在矩形内,矩形中未被覆盖的部分用阴影表示,设左上角与右下角的阴影部分的面积相等.设.若,k为整数,则a可取的值的个数为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.0个 B.4个 C.5个 D.无数个
3.如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到△ECF.若BC=1,则△ECF的周长为( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A. B. C. D.
4.一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )
A.y=x(15-x) B.y=x(30-x) C.y=x(30-2x) D.y=x(15+x)
5.一个四边形要成为矩形,需要的条件是( )
A.两个内角相等 B.三个内角相等
C.四个内角相等 D.两个外角为直角
6.如图,将一张长方形纸片 ( http: / / www.21cnjy.com )ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,那么∠ADB的度数是( )
( http: / / www.21cnjy.com / )
A.18° B.20° C.36° D.45°
7.在□ABCD中,AB=3, ( http: / / www.21cnjy.com )BC=4,当口ABCD的面积最大时,下列结论:①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.其中正确的有( )21cnjy.com
A.①②③ B.①②④ C.②③④ D.①③④
8.如图,在矩形ABCD中,AB=2 ( http: / / www.21cnjy.com ),BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点E,EF⊥BD于点F,则OE+EF的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B.2 C. D.2
9.如图,在矩形 中, , 相交于点O,若 的面积是3,则矩形 的面积是( ) 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( ) 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.1:3 B.2:3 C.1:2 D.1:4
二、填空题
11.如图,将矩形ABCD沿AC折叠,使点B落在点B'处,B'C交AD于点E,若∠1=25°,则∠2的度数为 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
12.如图, AFDE的顶点F在矩形ABCD ( http: / / www.21cnjy.com )的边BC上,点F与点B、C不重合,若△AED的面积为4,则图中阴影部分两个三角形的面积和为 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
13.如图,在中,,,,点P是AB上的任意一点,作于点D,于点E,连接DE,则DE的最小值为 .21*cnjy*com
( http: / / www.21cnjy.com / )
14.有一架竖直靠在直角墙面 ( http: / / www.21cnjy.com )的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M,N分别在墙面BA,BC上,梯子MN的长度始终保持不变,MN=2,老鼠E在MN的中点处,猫在D点处,它到墙面BA,BC的距离分别为2和1.在此滑动过程中,猫与老鼠的距离DE的最小值为 .【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
15.如图,∠MON=90°,矩形 ( http: / / www.21cnjy.com )ABCD的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,点A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=3.运动过程中点D到点O的最大距离是 .
( http: / / www.21cnjy.com / )
16.如图,长方形纸片AB ( http: / / www.21cnjy.com )CD中,AB=8cm,BC=17cm,点O在边BC上,且OB=10cm.将纸片沿过点O的直线折叠,若点B恰好落在边AD上的点F处,则AF的长为 cm.
( http: / / www.21cnjy.com / )
17.如图,在长方形ABCD中,AB=3,BC=2,E是BC中点,点F是线段AB上一个动点.
( http: / / www.21cnjy.com / )
(1)连接DF,则DF+EF的最小值为 ;
(2)以EF为斜边向斜上方作等腰Rt△EFG,点F从点B运动到点A的过程中,AG的最小值为 .
18.如图,矩形ABCD的边CD上有一点E, , ,垂足为F,将 绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:① ;②四边形EFBC是正方形;③ ;④ ,其中结论正确的为 .(填写序号即可)
( http: / / www.21cnjy.com / )
三、解答题
19.某同学对矩形纸片ABCD进行了如下的操作:如图,先沿直线AG折叠,使点B落在对角线AC上的点P处,再沿直线CH折叠,使点D落在AC上的点Q处.若 , ,求四边形 的面积. 21教育名师原创作品
( http: / / www.21cnjy.com / )
20.一次数学课上,老师请同学们在一 ( http: / / www.21cnjy.com )张长为18cm.宽为16cm的矩形纸板上,剪下一个腰长为10cm的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其他两个顶点在矩形的边上,求剪下的等腰三角形的面积.21·cn·jy·com
( http: / / www.21cnjy.com / )
21.如图,在四边形中,.点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使和,分别需经过多少时间?为什么?
( http: / / www.21cnjy.com / )
22.在Rt△ABC中,∠C=90°,D,E,F分别是AC,AB,BC的中点,连接ED,EF.求证:四边形DEFC是矩形.21*cnjy*com
( http: / / www.21cnjy.com / )
23.如图,在矩形 中, ,且交 的延长线于点 .求证: .
( http: / / www.21cnjy.com / )
24.操作:第一步:如图1,对折长方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开.
( http: / / www.21cnjy.com / )
第二步:如图2,再一次折叠纸片 ( http: / / www.21cnjy.com ),使点A落在EF上的N处,并使折痕经过点B,得到折痕BM,同时得到线段BN.连结AN,易知△ABN的形状是 ▲ .2·1·c·n·j·y
论证:如图3,若延长MN交BC于点P,试判定△BMP的形状,请说明理由.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】A
11.【答案】50°
12.【答案】4
13.【答案】2.4
14.【答案】
15.【答案】
16.【答案】16
17.【答案】(1)
(2)
18.【答案】①②④
19.【答案】解:∵四边形ABCD是矩形, , ,
∴ , ,
∴ ,
由折叠的性质可知AP=AB=5,BG=PG,∠B=∠APG=90°,CQ=CD=5,
∴CP=8,∠CPG=90°,
设CG=x,则BG=PG=12-x,
∴由勾股定理可得: ,
解得: ,
即CG=,同理AH=,
∴CG=AH,
∵四边形ABCD是矩形,
∴AD∥BC,
∴四边形AGCH是平行四边形,21教育网
∴ .
20.【答案】解:分三种情况.
①如图1,在△AEF中,AE=AF=10cm,
( http: / / www.21cnjy.com / )
∴
②如图2,在△AGH中,AG=GH=10cm,
( http: / / www.21cnjy.com / )
∴BG=AB-AG=16-10=6(cm).
根据勾股定理,得BH=8cm,
∴
③如图3,在 中, ,
( http: / / www.21cnjy.com / )
∴ .
根据勾股定理,得DN=6cm,
∴
综上所述,剪下的等腰三角形的面积为50cm2或40cm2或30cm2.
21.【答案】解:①设经过,,
此时四边形成为平行四边形,
∵,
∴,
解得,
∴当s时,且PQ=CD
②设经过,,
如图所示,分别过点P,D作BC边的垂线PE,DF,垂足分别为E,F,当CF=EQ时,四边形PQCD为梯形(腰相等)或平行四边形,www.21-cn-jy.com
( http: / / www.21cnjy.com / )
∵,
∴四边形ABFD是矩形,
∴AD=BF,
∵AD=24cm,BC=26cm,
∴(cm),
当四边形PQCD为梯形(腰相等)时,,
∴,
解得,
∴当s时,PQ=CD,
当四边形为平行四边形或梯形(腰相等),为平行四边形时有s,PQ=CD,
综上所述,当s时,;当s或s时,PQ=CD.
22.【答案】证明:∵D,E,F分别是AC,AB,BC的中点,
∴DE∥FC,EF∥CD,
∴四边形DEFC是平行四边形,
∵∠DCF=90°,
∴四边形DEFC是矩形.
23.【答案】证明:∵四边形 是矩形,
∴ , .
∵
∴四边形 是平行四边形.
∴
24.【答案】解:等边三角形;论证:△BMP是等边三角形,理由如下:
如图3,∵△ABN是等边三角形,
∴∠ABN=60°,
∴∠NBM=∠ABM=∠ABN=30°,
∵∠NBP=∠ABP﹣∠ABN=30°,∠BNP=90°,
∴∠BPM=∠MBP=60°,
∴△BMP是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
