人教版数学八年级下册18.2.2菱形 同步课堂小测(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.2菱形 同步课堂小测(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 23:08:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册18.2.2菱形小测
一、单选题
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.下列命题中,假命题是( )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.矩形的对角线相等
D.正方形的对角线互相垂直平分
3.菱形ABCD的边长AB=5,则此菱形的周长是( )
A.20 B.25 C.10 D.5
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为边AD的中点,若,则菱形ABCD的周长为( )21cnjy.com
( http: / / www.21cnjy.com / )
A. B. C. D.
5.若顺次连接四边形各边中点所得的四边形是菱形,则原四边形( )
A.一定是矩形 B.一定是菱形
C.对角线一定互相垂直 D.对角线一定相等
6.已知平行四边形ABCD,下列叙述中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
7.如图,四边形 的对角线互相平分,要使它变为菱形,需要添加的条件是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
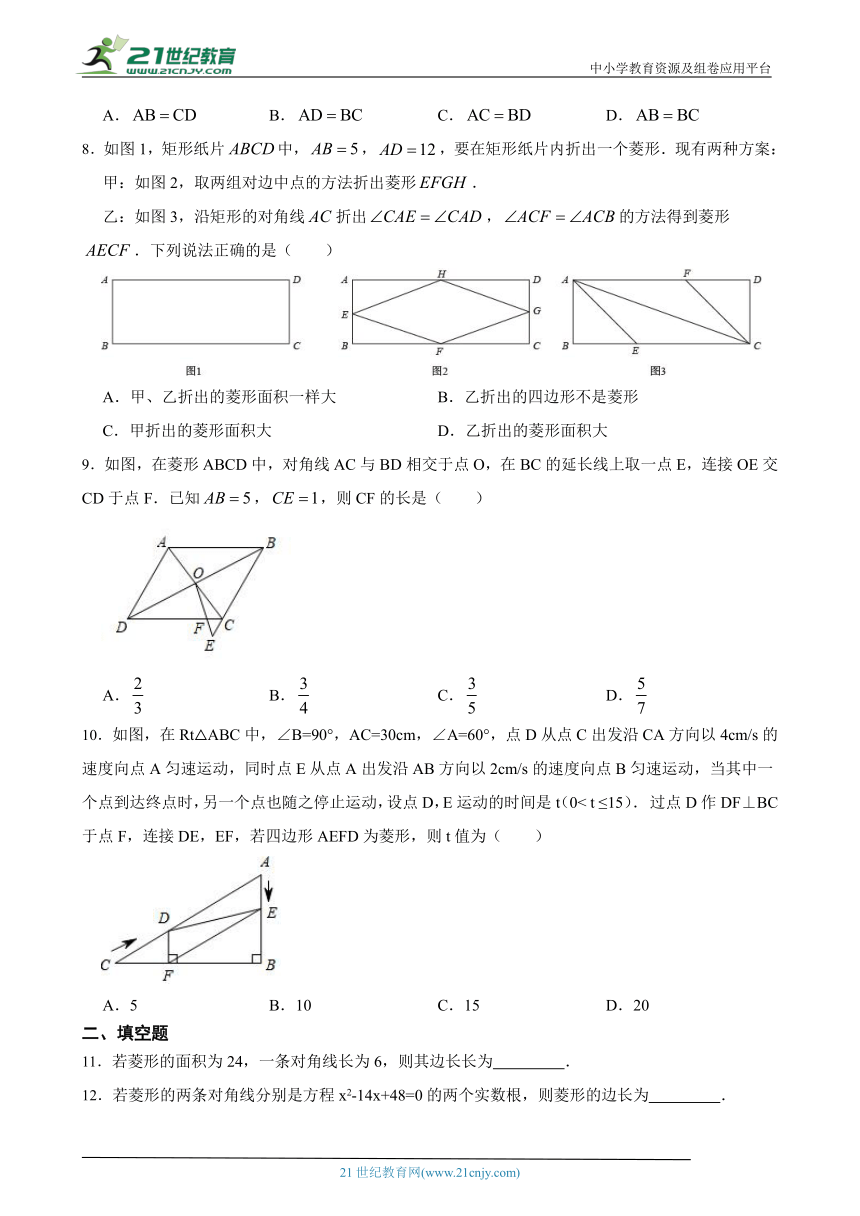
8.如图1,矩形纸片中,,,要在矩形纸片内折出一个菱形.现有两种方案:
甲:如图2,取两组对边中点的方法折出菱形.
乙:如图3,沿矩形的对角线折出,的方法得到菱形.下列说法正确的是( )
( http: / / www.21cnjy.com / )
A.甲、乙折出的菱形面积一样大 B.乙折出的四边形不是菱形
C.甲折出的菱形面积大 D.乙折出的菱形面积大
9.如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知,,则CF的长是( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在Rt△ABC中 ( http: / / www.21cnjy.com ),∠B=90°,AC=30cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0< t ≤15). 过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.5 B.10 C.15 D.20
二、填空题
11.若菱形的面积为24,一条对角线长为6,则其边长长为 .
12.若菱形的两条对角线分别是方程x2-14x+48=0的两个实数根,则菱形的边长为 .
13.如图,在菱形ABCD中,,,垂足分别为点E,F.若,则等于 度.
( http: / / www.21cnjy.com / )
14.已知菱形的两条对角线的长分别是10㎝和24㎝,那么菱形的每条边长是 .
15.如图,已知点A的坐标是,,点B的坐标是,,菱形的对角线交于坐标原点O,则点D的坐标是 .www.21-cn-jy.com
( http: / / www.21cnjy.com / )
16.如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 . 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
17.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角度数,正方形ABCD变为菱形 ,若 ,且菱形 的面积为16,则正方形ABCD的面积为 . 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
18.如图,AB∥CD,AC平分 ( http: / / www.21cnjy.com )∠BAD,BD平分∠ADC,AC和BD交于点E,F,G分别是线段AB和线段AC上的动点,且AF=CG,若DE=1,AB=2,则DF+DG的最小值为 .
( http: / / www.21cnjy.com / )
三、解答题
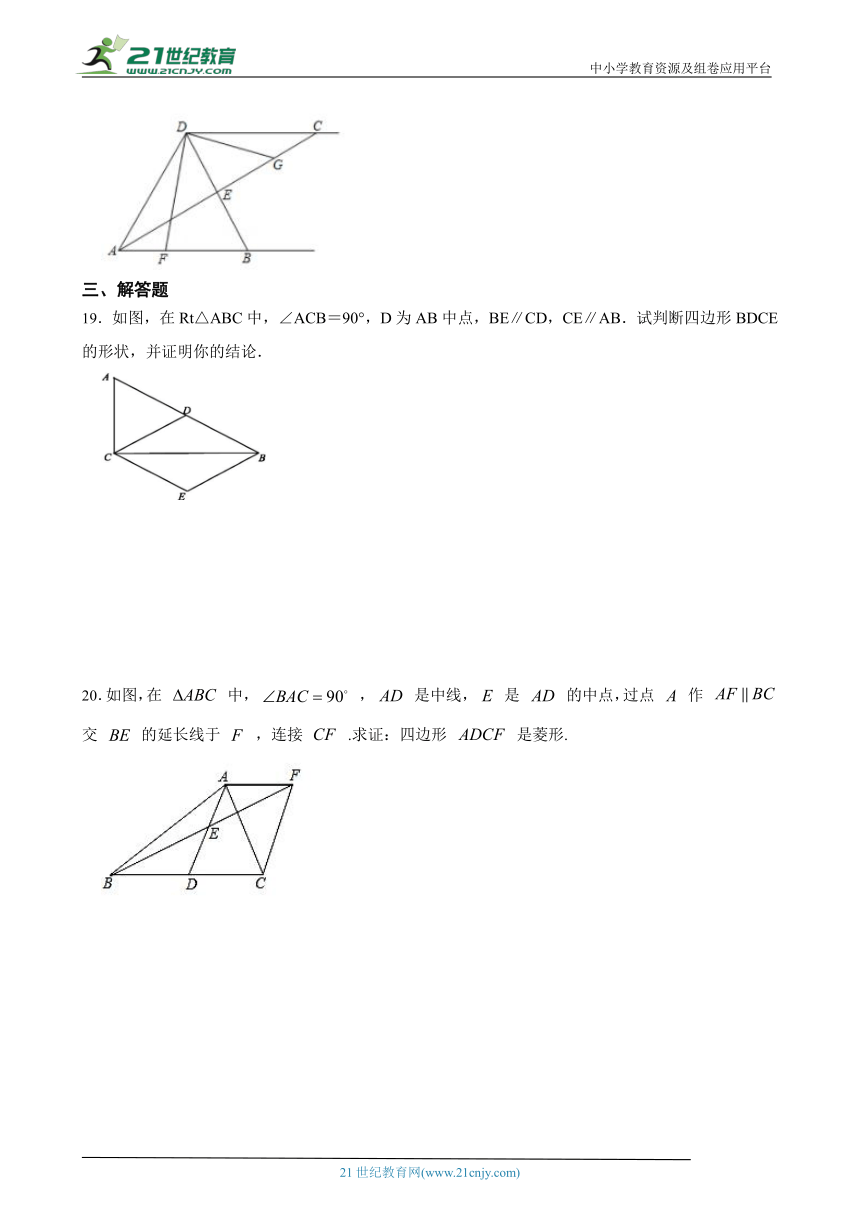
19.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,BE∥CD,CE∥AB.试判断四边形BDCE的形状,并证明你的结论.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
20.如图,在 中, , 是中线, 是 的中点,过点 作 交 的延长线于 ,连接 .求证:四边形 是菱形. 21*cnjy*com
( http: / / www.21cnjy.com / )
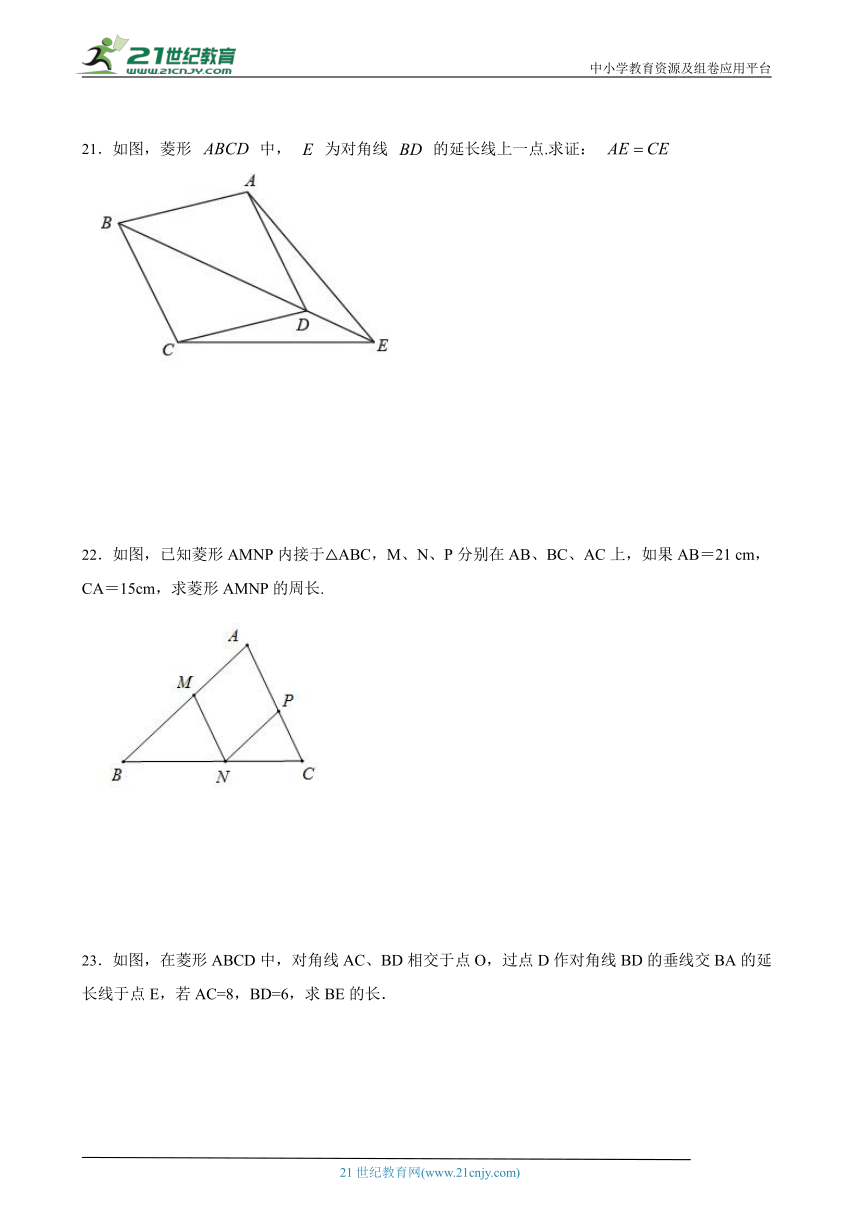
21.如图,菱形 中, 为对角线 的延长线上一点.求证:
( http: / / www.21cnjy.com / )
22.如图,已知菱形AMNP内接于△ABC ( http: / / www.21cnjy.com ),M、N、P分别在AB、BC、AC上,如果AB=21 cm,CA=15cm,求菱形AMNP的周长.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E,若AC=8,BD=6,求BE的长.21教育网
( http: / / www.21cnjy.com / )
24.如图,在菱形 中, 、 分别为边 和 上的点,且 .连接 、 交于点 .求证: . 21·世纪*教育网
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】A
11.【答案】5
12.【答案】5
13.【答案】50
14.【答案】13cm
15.【答案】
16.【答案】
17.【答案】32
18.【答案】
19.【答案】解:四边形BDCE 是菱形,理由如下:
∵BE ∥CD, CE∥AB ,
∴四边形BDCE 是平行四边形,
∵∠ACB=90°,D 为AB 中点,
CD=BD,
四边形BDCE 是菱形.
20.【答案】证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵AD是BC边上的中线
∴DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90 ,AD是BC边上的中线,
∴AD=DC= BC,
∴ ADCF是菱形.
21.【答案】证明: 四边形 是菱形,
, .
又 ,
.
22.【答案】解:∵AMNP是菱形,
∴PN//AB,∴△CPN∽△CAB,
∴CP:CA=PN:AB,
∵PN=PA,∴CP:CA=PA:AB,
即CP:15=PA:21,
∴CP:PA=15:21=5:7,
∴(CP+PA):PA=(5+7):7,
∴AC:PA=12:7,
即15:PA=12:7,
解得PA= ,
∴菱形AMNP的周长是: ×4=35cm
23.【答案】解:∵四边形ABCD是菱形,
( http: / / www.21cnjy.com / )
∴∠AOB=90°,AB∥CD,
∵DE⊥BD,
∴∠EDB=90°,
∴∠AOB=∠EDB,
∴ED∥AC,
∴四边形ACDE是平行四边形,
∴ED=AC=8,
在直角三角形BDE中, .
24.【答案】证明:∵四边形ABCD是菱形,
∴DA=DC=AB=BC,
∵AE=CF,
∴DE=DF
在△DAF和△DCE中,
,
∴△DAF≌△DCE(SAS),
∴∠EAG=∠FCG,
在△AEG和△CFG中,
,
∴△AEG≌△CFG(AAS),
∴EG=FG,
在△DGE和△DGF中,
,
∴△DGE≌△DGF(SSS),
∴∠DGE=∠DGF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册18.2.2菱形小测
一、单选题
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.下列命题中,假命题是( )
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.矩形的对角线相等
D.正方形的对角线互相垂直平分
3.菱形ABCD的边长AB=5,则此菱形的周长是( )
A.20 B.25 C.10 D.5
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为边AD的中点,若,则菱形ABCD的周长为( )21cnjy.com
( http: / / www.21cnjy.com / )
A. B. C. D.
5.若顺次连接四边形各边中点所得的四边形是菱形,则原四边形( )
A.一定是矩形 B.一定是菱形
C.对角线一定互相垂直 D.对角线一定相等
6.已知平行四边形ABCD,下列叙述中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
7.如图,四边形 的对角线互相平分,要使它变为菱形,需要添加的条件是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图1,矩形纸片中,,,要在矩形纸片内折出一个菱形.现有两种方案:
甲:如图2,取两组对边中点的方法折出菱形.
乙:如图3,沿矩形的对角线折出,的方法得到菱形.下列说法正确的是( )
( http: / / www.21cnjy.com / )
A.甲、乙折出的菱形面积一样大 B.乙折出的四边形不是菱形
C.甲折出的菱形面积大 D.乙折出的菱形面积大
9.如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知,,则CF的长是( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在Rt△ABC中 ( http: / / www.21cnjy.com ),∠B=90°,AC=30cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0< t ≤15). 过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t值为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.5 B.10 C.15 D.20
二、填空题
11.若菱形的面积为24,一条对角线长为6,则其边长长为 .
12.若菱形的两条对角线分别是方程x2-14x+48=0的两个实数根,则菱形的边长为 .
13.如图,在菱形ABCD中,,,垂足分别为点E,F.若,则等于 度.
( http: / / www.21cnjy.com / )
14.已知菱形的两条对角线的长分别是10㎝和24㎝,那么菱形的每条边长是 .
15.如图,已知点A的坐标是,,点B的坐标是,,菱形的对角线交于坐标原点O,则点D的坐标是 .www.21-cn-jy.com
( http: / / www.21cnjy.com / )
16.如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 . 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
17.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角度数,正方形ABCD变为菱形 ,若 ,且菱形 的面积为16,则正方形ABCD的面积为 . 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
18.如图,AB∥CD,AC平分 ( http: / / www.21cnjy.com )∠BAD,BD平分∠ADC,AC和BD交于点E,F,G分别是线段AB和线段AC上的动点,且AF=CG,若DE=1,AB=2,则DF+DG的最小值为 .
( http: / / www.21cnjy.com / )
三、解答题
19.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,BE∥CD,CE∥AB.试判断四边形BDCE的形状,并证明你的结论.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
20.如图,在 中, , 是中线, 是 的中点,过点 作 交 的延长线于 ,连接 .求证:四边形 是菱形. 21*cnjy*com
( http: / / www.21cnjy.com / )
21.如图,菱形 中, 为对角线 的延长线上一点.求证:
( http: / / www.21cnjy.com / )
22.如图,已知菱形AMNP内接于△ABC ( http: / / www.21cnjy.com ),M、N、P分别在AB、BC、AC上,如果AB=21 cm,CA=15cm,求菱形AMNP的周长.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E,若AC=8,BD=6,求BE的长.21教育网
( http: / / www.21cnjy.com / )
24.如图,在菱形 中, 、 分别为边 和 上的点,且 .连接 、 交于点 .求证: . 21·世纪*教育网
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】D
10.【答案】A
11.【答案】5
12.【答案】5
13.【答案】50
14.【答案】13cm
15.【答案】
16.【答案】
17.【答案】32
18.【答案】
19.【答案】解:四边形BDCE 是菱形,理由如下:
∵BE ∥CD, CE∥AB ,
∴四边形BDCE 是平行四边形,
∵∠ACB=90°,D 为AB 中点,
CD=BD,
四边形BDCE 是菱形.
20.【答案】证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵AD是BC边上的中线
∴DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90 ,AD是BC边上的中线,
∴AD=DC= BC,
∴ ADCF是菱形.
21.【答案】证明: 四边形 是菱形,
, .
又 ,
.
22.【答案】解:∵AMNP是菱形,
∴PN//AB,∴△CPN∽△CAB,
∴CP:CA=PN:AB,
∵PN=PA,∴CP:CA=PA:AB,
即CP:15=PA:21,
∴CP:PA=15:21=5:7,
∴(CP+PA):PA=(5+7):7,
∴AC:PA=12:7,
即15:PA=12:7,
解得PA= ,
∴菱形AMNP的周长是: ×4=35cm
23.【答案】解:∵四边形ABCD是菱形,
( http: / / www.21cnjy.com / )
∴∠AOB=90°,AB∥CD,
∵DE⊥BD,
∴∠EDB=90°,
∴∠AOB=∠EDB,
∴ED∥AC,
∴四边形ACDE是平行四边形,
∴ED=AC=8,
在直角三角形BDE中, .
24.【答案】证明:∵四边形ABCD是菱形,
∴DA=DC=AB=BC,
∵AE=CF,
∴DE=DF
在△DAF和△DCE中,
,
∴△DAF≌△DCE(SAS),
∴∠EAG=∠FCG,
在△AEG和△CFG中,
,
∴△AEG≌△CFG(AAS),
∴EG=FG,
在△DGE和△DGF中,
,
∴△DGE≌△DGF(SSS),
∴∠DGE=∠DGF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
