人教版数学八年级下册18.2.3 正方形 同步课堂小测(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.3 正方形 同步课堂小测(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 23:07:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册18.2.3正方形小测
一、单选题
1.若一个正方形的面积是28,则它的边长为( )
A. B. C. D.
2.下列条件中,能判定四边形是正方形的是( )
A.对角线相等的平行四边形
B.对角线互相平分且垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等且互相垂直的平行四边形
3.如图.已知正方形AB ( http: / / www.21cnjy.com )CD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论;①AG+EC=GE;②∠GDE=45°;③△BGE的周长是24.其中正确的个数为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.0 B.1 C.2 D.3
4.在边长为2的正方形ABCD中,E、F分别为DC、BC上的点,且DE=CF,连接DF,BE,求DF+BE的最小值为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C.4 D.
5.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
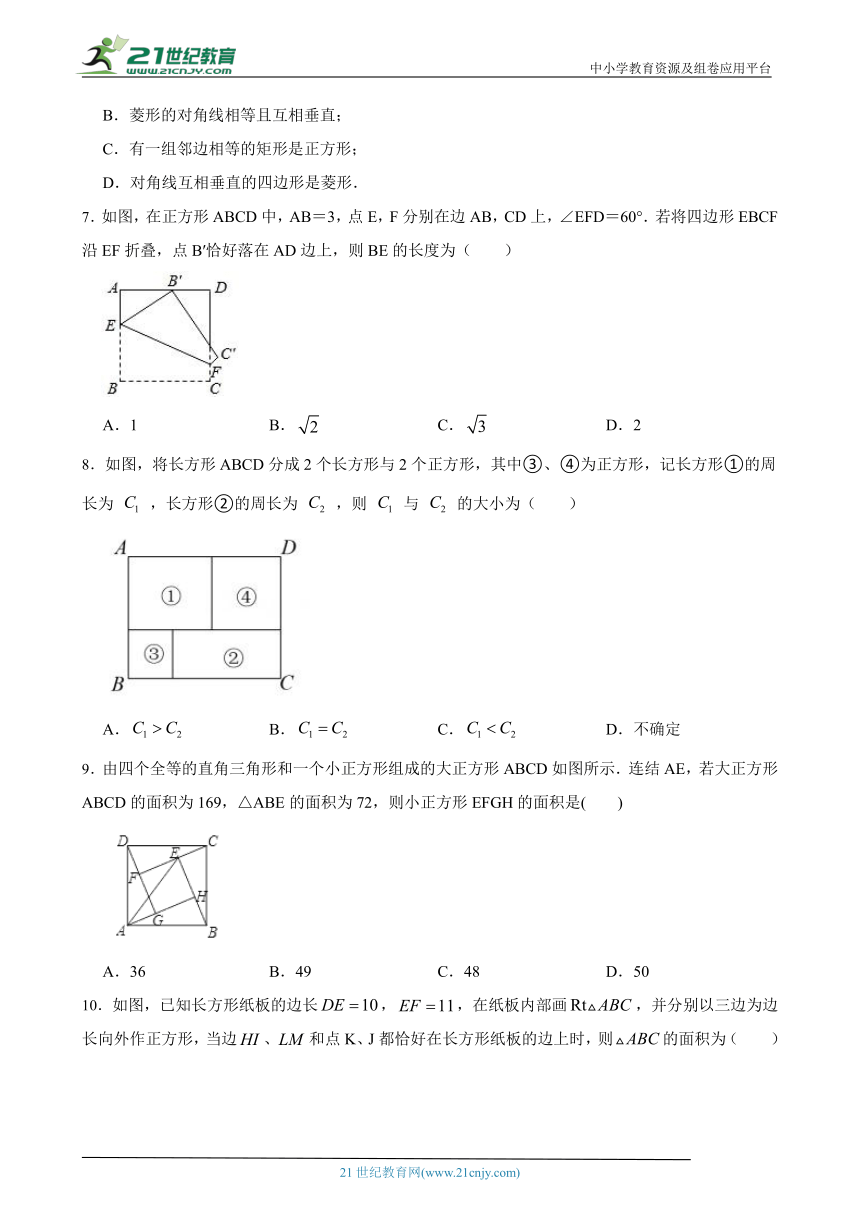
6.下列说法中正确的是( )
A.矩形的对角线平分每组对角;
B.菱形的对角线相等且互相垂直;
C.有一组邻边相等的矩形是正方形;
D.对角线互相垂直的四边形是菱形.
7.如图,在正方形ABCD中,AB=3,点E ( http: / / www.21cnjy.com ),F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B′恰好落在AD边上,则BE的长度为( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.1 B. C. D.2
8.如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为 ,长方形②的周长为 ,则 与 的大小为( ) 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.不确定
9.由四个全等的直角三角形 ( http: / / www.21cnjy.com )和一个小正方形组成的大正方形ABCD如图所示.连结AE,若大正方形ABCD的面积为169,△ABE的面积为72,则小正方形EFGH的面积是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.36 B.49 C.48 D.50
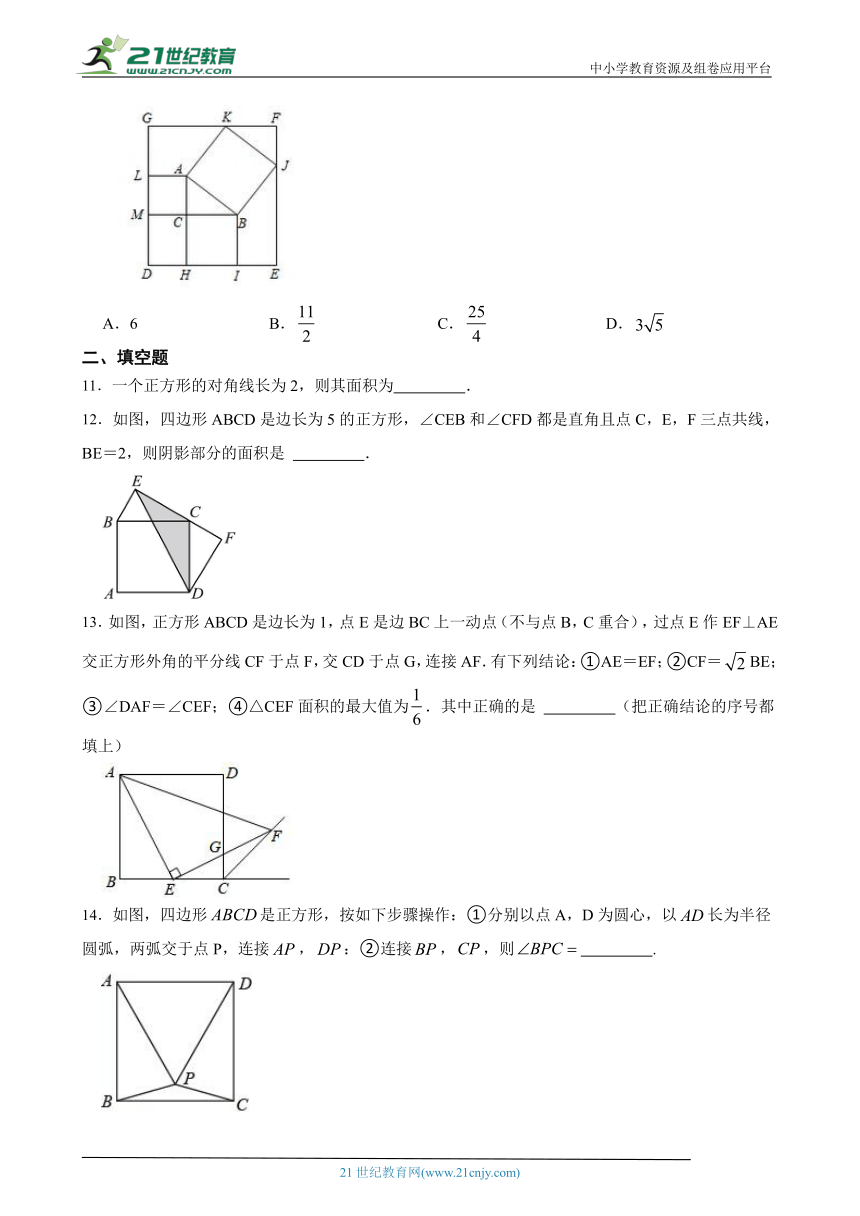
10.如图,已知长方形纸板的边长,,在纸板内部画,并分别以三边为边长向外作正方形,当边、和点K、J都恰好在长方形纸板的边上时,则的面积为( )
( http: / / www.21cnjy.com / )
A.6 B. C. D.
二、填空题
11.一个正方形的对角线长为2,则其面积为 .
12.如图,四边形ABCD是边长为5的正 ( http: / / www.21cnjy.com )方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 .21教育网
( http: / / www.21cnjy.com / )
13.如图,正方形ABCD是边长为1,点E是边BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:①AE=EF;②CF=BE;③∠DAF=∠CEF;④△CEF面积的最大值为.其中正确的是 (把正确结论的序号都填上)21·世纪*教育网
( http: / / www.21cnjy.com / )
14.如图,四边形是正方形,按如下步骤操作:①分别以点A,D为圆心,以长为半径圆弧,两弧交于点P,连接,:②连接,,则 .
( http: / / www.21cnjy.com / )
15.如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
( http: / / www.21cnjy.com / )
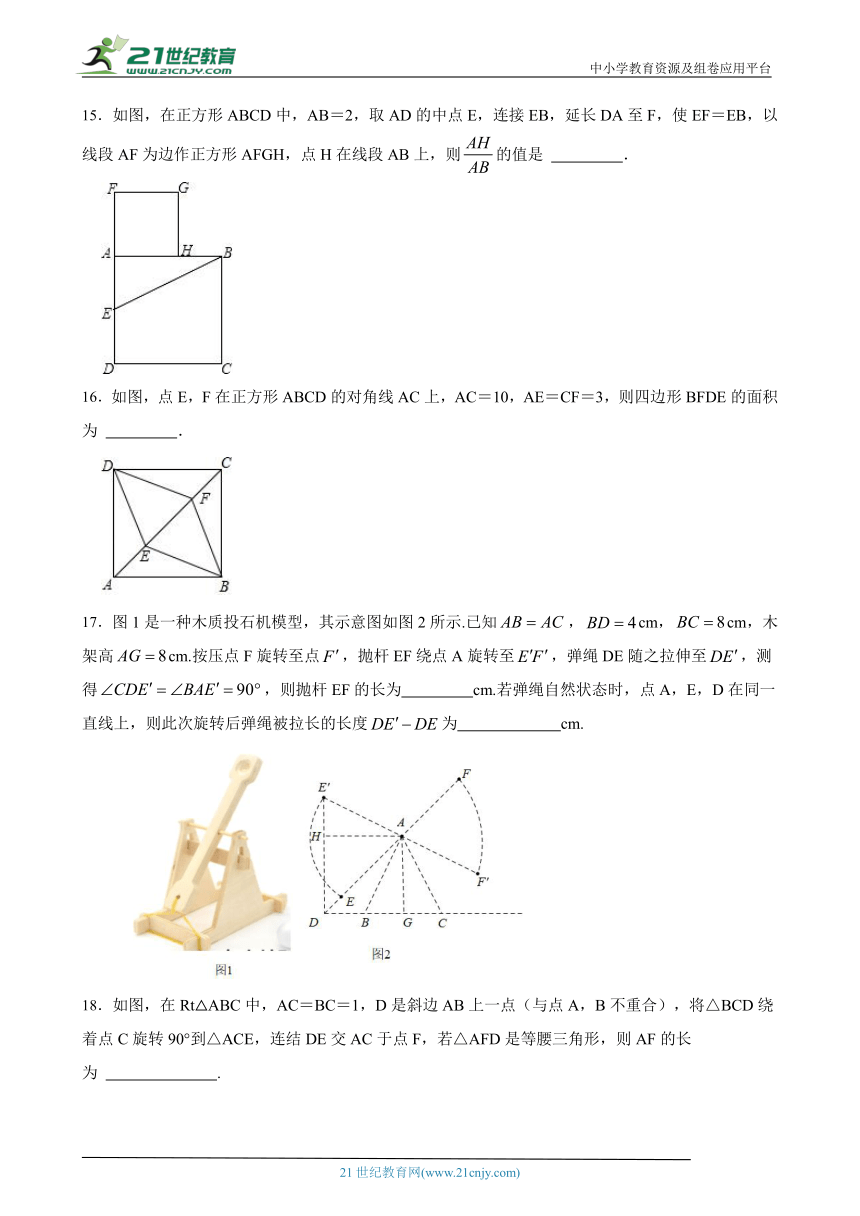
16.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
17.图1是一种木质投石机模型,其示意图如图2所示.已知,cm,cm,木架高cm.按压点F旋转至点,抛杆EF绕点A旋转至,弹绳DE随之拉伸至,测得,则抛杆EF的长为 cm.若弹绳自然状态时,点A,E,D在同一直线上,则此次旋转后弹绳被拉长的长度为 cm.2-1-c-n-j-y
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
18.如图,在Rt△AB ( http: / / www.21cnjy.com )C中,AC=BC=1,D是斜边AB上一点(与点A,B不重合),将△BCD绕着点C旋转90°到△ACE,连结DE交AC于点F,若△AFD是等腰三角形,则AF的长为 .
( http: / / www.21cnjy.com / )
三、解答题
19.一个正方形的边长增加2cm,它的面积就增加了24cm ,这个正方形原来的边长是多少
20.小田同学用一根长为120cm的铁丝分成两段,分别用来围成两个面积之比为4:1的正方形,求较大的正方形的边长为多少?21cnjy.com
21.如图,在正方形 中,点E、F分别在 上,且 是等边三角形.
( http: / / www.21cnjy.com / )
求证: .
22.如图,正方形 的对角线 、 相交于点 , 、 分别在 、 上, .写出 与 的关系,并说明理由. 21*cnjy*com
( http: / / www.21cnjy.com / )
23.如图,四边形 是边长为9的正方形纸片,将其沿 折叠,使点B落在 边上的点 处,点A的对应点为点 ,且 ,求 的长. 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
24.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,
( http: / / www.21cnjy.com / )
(1)连接AC、BD,由三角形中位线的性质定理可证四边形EFGH是 ;
(2)对角线AC、BD满足条件 时,四边形EFGH是矩形;
(3)对角线AC、BD满足条件 时,四边形EFGH是菱形;
(4)对角线AC、BD满足条件 时,四边形EFGH是正方形.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】2
12.【答案】
13.【答案】①②
14.【答案】150
15.【答案】
16.【答案】20
17.【答案】;
18.【答案】或
19.【答案】解:设原来正方形的边长为 ,增加后边长则为 ,
根据题意得: ,
利用平方差公式展开得:
解得: ,
则这个正方形原来的边长为5cm
20.【答案】解:设较大正方形的边长为 ,较小正方形的边长为y,
根据题意得: ,
由 可得 ,
将 代入 中得: ,
整理得: ,
解得: , (舍),
所以较大正方形的边长为 .
21.【答案】证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠C=90°,
∵△BEF是等边三角形,
∴BE=BF,
在Rt△ABF和Rt△CBE中,
,
∴Rt△ABF≌Rt△CBE(HL),
∴AF=CE,
∴CD-CE=AD-AF,
∴DE=DF.
22.【答案】解: ,且 ,理由如下:
延长 交 于 ,如图:
( http: / / www.21cnjy.com / )
∵四边形 为正方形,
∴ , ,
在 和 中,
,
∴ ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∴ .
23.【答案】解:设 ,
连接 , ,
( http: / / www.21cnjy.com / )
在 中, ,
在 中, ,
∵ ,
∴ ,
即 ,
解得 ,
即 .
24.【答案】(1)平行四边形
(2)AC⊥BD
(3)AC=BD
(4)AC⊥BD且AC=BD
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册18.2.3正方形小测
一、单选题
1.若一个正方形的面积是28,则它的边长为( )
A. B. C. D.
2.下列条件中,能判定四边形是正方形的是( )
A.对角线相等的平行四边形
B.对角线互相平分且垂直的四边形
C.对角线互相垂直且相等的四边形
D.对角线相等且互相垂直的平行四边形
3.如图.已知正方形AB ( http: / / www.21cnjy.com )CD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论;①AG+EC=GE;②∠GDE=45°;③△BGE的周长是24.其中正确的个数为( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.0 B.1 C.2 D.3
4.在边长为2的正方形ABCD中,E、F分别为DC、BC上的点,且DE=CF,连接DF,BE,求DF+BE的最小值为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C.4 D.
5.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
6.下列说法中正确的是( )
A.矩形的对角线平分每组对角;
B.菱形的对角线相等且互相垂直;
C.有一组邻边相等的矩形是正方形;
D.对角线互相垂直的四边形是菱形.
7.如图,在正方形ABCD中,AB=3,点E ( http: / / www.21cnjy.com ),F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B′恰好落在AD边上,则BE的长度为( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.1 B. C. D.2
8.如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为 ,长方形②的周长为 ,则 与 的大小为( ) 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.不确定
9.由四个全等的直角三角形 ( http: / / www.21cnjy.com )和一个小正方形组成的大正方形ABCD如图所示.连结AE,若大正方形ABCD的面积为169,△ABE的面积为72,则小正方形EFGH的面积是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.36 B.49 C.48 D.50
10.如图,已知长方形纸板的边长,,在纸板内部画,并分别以三边为边长向外作正方形,当边、和点K、J都恰好在长方形纸板的边上时,则的面积为( )
( http: / / www.21cnjy.com / )
A.6 B. C. D.
二、填空题
11.一个正方形的对角线长为2,则其面积为 .
12.如图,四边形ABCD是边长为5的正 ( http: / / www.21cnjy.com )方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 .21教育网
( http: / / www.21cnjy.com / )
13.如图,正方形ABCD是边长为1,点E是边BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF.有下列结论:①AE=EF;②CF=BE;③∠DAF=∠CEF;④△CEF面积的最大值为.其中正确的是 (把正确结论的序号都填上)21·世纪*教育网
( http: / / www.21cnjy.com / )
14.如图,四边形是正方形,按如下步骤操作:①分别以点A,D为圆心,以长为半径圆弧,两弧交于点P,连接,:②连接,,则 .
( http: / / www.21cnjy.com / )
15.如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
( http: / / www.21cnjy.com / )
16.如图,点E,F在正方形ABCD的对角线AC上,AC=10,AE=CF=3,则四边形BFDE的面积为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
17.图1是一种木质投石机模型,其示意图如图2所示.已知,cm,cm,木架高cm.按压点F旋转至点,抛杆EF绕点A旋转至,弹绳DE随之拉伸至,测得,则抛杆EF的长为 cm.若弹绳自然状态时,点A,E,D在同一直线上,则此次旋转后弹绳被拉长的长度为 cm.2-1-c-n-j-y
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
18.如图,在Rt△AB ( http: / / www.21cnjy.com )C中,AC=BC=1,D是斜边AB上一点(与点A,B不重合),将△BCD绕着点C旋转90°到△ACE,连结DE交AC于点F,若△AFD是等腰三角形,则AF的长为 .
( http: / / www.21cnjy.com / )
三、解答题
19.一个正方形的边长增加2cm,它的面积就增加了24cm ,这个正方形原来的边长是多少
20.小田同学用一根长为120cm的铁丝分成两段,分别用来围成两个面积之比为4:1的正方形,求较大的正方形的边长为多少?21cnjy.com
21.如图,在正方形 中,点E、F分别在 上,且 是等边三角形.
( http: / / www.21cnjy.com / )
求证: .
22.如图,正方形 的对角线 、 相交于点 , 、 分别在 、 上, .写出 与 的关系,并说明理由. 21*cnjy*com
( http: / / www.21cnjy.com / )
23.如图,四边形 是边长为9的正方形纸片,将其沿 折叠,使点B落在 边上的点 处,点A的对应点为点 ,且 ,求 的长. 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
24.如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,
( http: / / www.21cnjy.com / )
(1)连接AC、BD,由三角形中位线的性质定理可证四边形EFGH是 ;
(2)对角线AC、BD满足条件 时,四边形EFGH是矩形;
(3)对角线AC、BD满足条件 时,四边形EFGH是菱形;
(4)对角线AC、BD满足条件 时,四边形EFGH是正方形.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】2
12.【答案】
13.【答案】①②
14.【答案】150
15.【答案】
16.【答案】20
17.【答案】;
18.【答案】或
19.【答案】解:设原来正方形的边长为 ,增加后边长则为 ,
根据题意得: ,
利用平方差公式展开得:
解得: ,
则这个正方形原来的边长为5cm
20.【答案】解:设较大正方形的边长为 ,较小正方形的边长为y,
根据题意得: ,
由 可得 ,
将 代入 中得: ,
整理得: ,
解得: , (舍),
所以较大正方形的边长为 .
21.【答案】证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠A=∠C=90°,
∵△BEF是等边三角形,
∴BE=BF,
在Rt△ABF和Rt△CBE中,
,
∴Rt△ABF≌Rt△CBE(HL),
∴AF=CE,
∴CD-CE=AD-AF,
∴DE=DF.
22.【答案】解: ,且 ,理由如下:
延长 交 于 ,如图:
( http: / / www.21cnjy.com / )
∵四边形 为正方形,
∴ , ,
在 和 中,
,
∴ ,
∴ , ,
∵ , ,
∴ ,
∴ ,
∴ .
23.【答案】解:设 ,
连接 , ,
( http: / / www.21cnjy.com / )
在 中, ,
在 中, ,
∵ ,
∴ ,
即 ,
解得 ,
即 .
24.【答案】(1)平行四边形
(2)AC⊥BD
(3)AC=BD
(4)AC⊥BD且AC=BD
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
