第二十章 数据的分析单元检测卷(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册第二十章数据的分析单元检测卷
一、单选题
1.在一次素养比赛中,6位学生的 ( http: / / www.21cnjy.com )成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( ) 21世纪教育网版权所有
A.平均数 B.中位数 C.众数 D.方差
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( ) 21·世纪*教育网
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
3.下列统计量中,反映一组数据波动情况的是( )
A.方差 B.众数 C.频率 D.平均数
4.某小组9位同学的中考 ( http: / / www.21cnjy.com )体育测试成绩(满分40分)依次为36,40,39,36,40,38,40,39,40.则这组数据的众数与中位数分别是( )【来源:21·世纪·教育·网】
A.40,39 B.39,40 C.36,40 D.40,40
5.某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较两名同学成绩的( )www-2-1-cnjy-com
A.平均数 B.方差 C.频数分布 D.中位数
6.在对一组样本数据进行分析时,小 ( http: / / www.21cnjy.com )明列出了方差的计算公式: ,由公式提供的信息,判断下列关于样本的说法错误的是( ) 2-1-c-n-j-y
A.平均数是8 B.众数是6 C.中位数是9 D.方差是3.6
7.有一组数据为 , , , ,这组数据的每一个数都减去 后得一组新的数据 , , , ,这两组数据一定不变的是( )
A.中位数 B.众数 C.平均数 D.方差
8.某单位采购了5箱苹果,得到每箱质量各不相同的五个数据.登记入账时将最小的数据又少写了1,则计算结果不受影响的是( ) 21*cnjy*com
A.中位数 B.平均数 C.方差 D.标准差
9.学校为了丰富学生课余活动,开展了一次“爱我中华,唱我中华”的歌咏比赛,共有18名同学人围,他们的决赛成绩如下表: 21·cn·jy·com
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70分,9.60分 B.9.60分,9.60分
C.9.60分,9.70分 D.9.65分,9.60分
10.一城市准备选购一千株高 ( http: / / www.21cnjy.com )度大约为2m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度,得到的数据如下: 【来源:21cnj*y.co*m】
树苗平均高度(单位:m) 标准差
甲苗圃 1.8 0.2
乙苗圃 1.8 0.6
丙苗圃 2.0 0.6
丁苗圃 2.0 0.2
请你帮采购小组出谋划策,应选购( )
A.甲苗圃的树苗 B.乙苗圃的树苗;
C.丙苗圃的树苗 D.丁苗圃的树苗
二、填空题
11.某研究员随机从甲、乙两块试验田中各抽取100株杂交水稻苗测试高度,经测量、计算平均数和方差的结果为 =12cm, =12cm, , ,则杂交水稻长势比较整齐的是 试验田.(填“甲”或“乙”)www.21-cn-jy.com
12.有8个数的平均数是8,另外有12个数的平均数是9,这20个数的平均数是
13.下列五个数:11,12,13,14,15的标准差为
14.现有甲、乙两支排球队,每支球队队员身高的平均数均为1.82米,方差分别为=3.7,=4.2,则身高较整齐的球队是 队.
【出处:21教育名师】
15.某校拟招聘一批优秀教师,其中某位教师 ( http: / / www.21cnjy.com )笔试、试讲、面试三轮测试得分分别为95分、85分、90分,综合成绩笔试、试讲、面试的占比为2:2:1,则该名教师的综合成绩为 .
16.已知一组不全等的数据:x1, ( http: / / www.21cnjy.com )x2,x3,……,xn,平均数是2020,方差是2021,则新数据:2020,x1,x2,x3,……,xn的平均数是 ,方差 2021(填“=、>或<”).
17.为了践行“首都市民卫生健康公约”,某班级举办“七步洗手法”比赛活动,小明的单项成绩如表所示(各项成绩均按百分制计):【版权所有:21教育】
项目 书面测试 实际操作 宣传展示
成绩(分) 96 98 96
若按书面测试占30%、实际操作占50%、宣传展示占20%,计算参赛个人的综合成绩(百分制),则小明的最后得分是 .21教育名师原创作品
18.某村选用条件相同的各6块实验田播种 ( http: / / www.21cnjy.com )甲乙两种水稻良种,结果两种水稻的平均亩产量相同,方差:S2甲=143,S2乙=313,从产量稳定性考虑,适合推广的品种为 .(填“甲”或“乙”)
三、解答题
19.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果 的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示: 21*cnjy*com
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
请计算说明哪位选手成绩更优秀.
20.灯泡厂为测量一批灯泡的寿命,从中随机抽查了50只灯泡,它们的寿命如表所示:
使用寿命 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
这批灯泡的平均使用寿命是多少?
21.甲、乙两个小组各6名学生的英语口试测验成绩如下(单位:分).
甲组:76,90,88,82,85,83.
乙组:81,90,91,89,79,74.
请你利用统计知识,说明哪个小组学生的成绩比较稳定.
22.某校八(1)班开展男生、女生垫排球比赛活动,每队各派5名同学参加.下表是男生队和女生队5名同学的比赛数据(单位:个):21教育网
1号 2号 3号 4号 5号
男生队 100 98 110 89 103
女生队 88 100 95 120 97
请回答下列问题:
(1)计算两队的平均成绩;
(2)从成绩稳定性角度考虑,哪队成绩稍好,请说明理由.
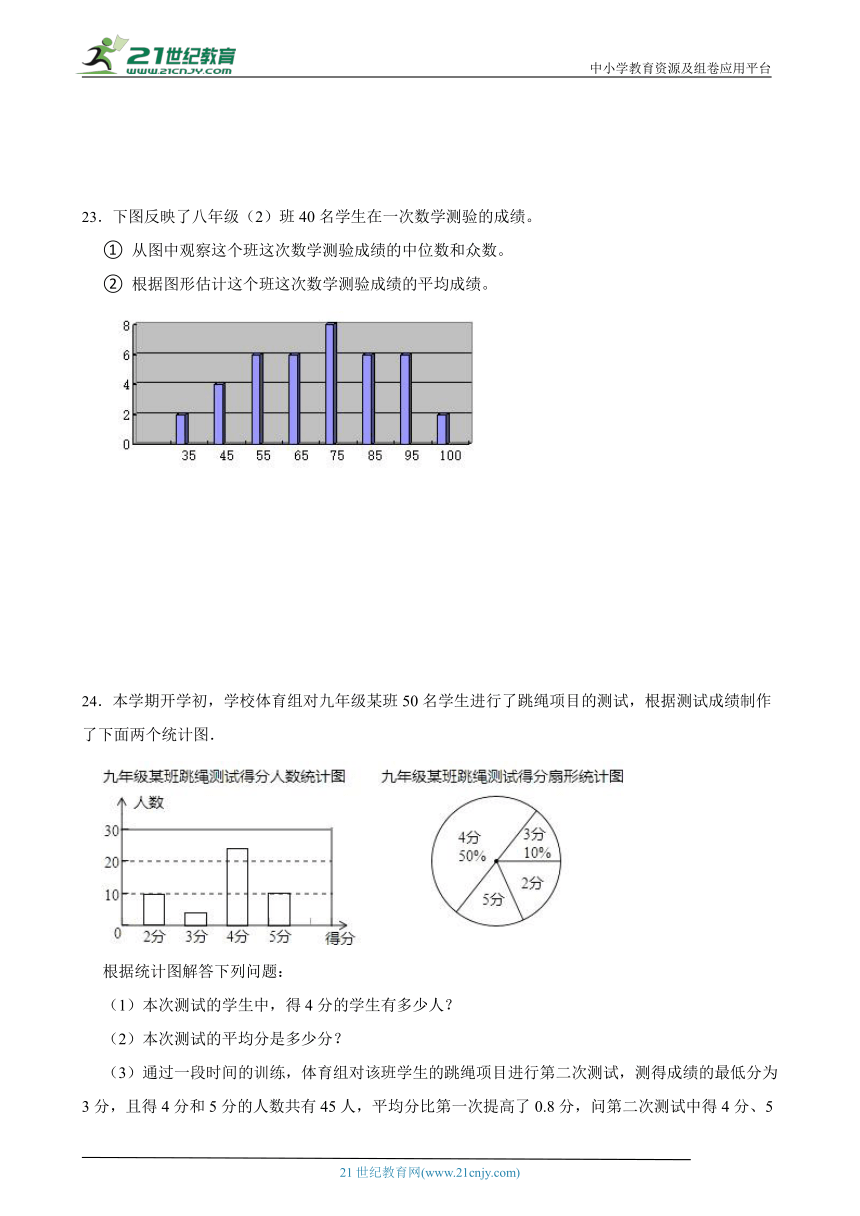
23.下图反映了八年级(2)班40名学生在一次数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位数和众数。
② 根据图形估计这个班这次数学测验成绩的平均成绩。
( http: / / www.21cnjy.com / )
24.本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.21cnjy.com
( http: / / www.21cnjy.com / )
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组 ( http: / / www.21cnjy.com )对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?2·1·c·n·j·y
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】甲
12.【答案】8.6
13.【答案】
14.【答案】甲
15.【答案】90分
16.【答案】2020;<
17.【答案】97
18.【答案】甲
19.【答案】解:根据题意得:
选手 的综合成绩为: 分,
选手 的综合成绩为: 分
∵
∴选手 的成绩更优秀.
20.【答案】解:平均使用寿命= ,
∴这批灯泡的平均使用寿命是1672.
21.【答案】解:甲组学生成绩的平均数 ;
乙组学生成绩的平均数 ;
甲组成绩的方差
;
乙组成绩的方差
;
,
甲小组学生的成绩比较稳定.
22.【答案】(1)解:男生队: =100(个);
女生队: =100(个).
(2)解: ;
∵ ,
∴男生队的成绩更稳定性,
即男生队成绩稍好.
23.【答案】解:①出现最多的是75分,有8个人,故众数为75(分);
总共有40人的数学成绩,第20、21位都是75分,则中位数为75(分)
②平均数=
估计这个班这次数学测验成绩的平均成绩为71.25.
24.【答案】(1)解:根据题意得:
得4分的学生有50×50%=25(人),
答:得4分的学生有25人
(2)解:根据题意得:
平均分= =3.7(分)
(3)解:设第二次测试中得4分的学生有x人,得5分的学生有y人,根据题意得:
,
解得: ,
答:第二次测试中得4分的学生有15人,得5分的学生有30人
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册第二十章数据的分析单元检测卷
一、单选题
1.在一次素养比赛中,6位学生的 ( http: / / www.21cnjy.com )成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( ) 21世纪教育网版权所有
A.平均数 B.中位数 C.众数 D.方差
2.2022年2月20日,北京冬奥会圆满闭幕,冬奥会的部分金牌榜如表所示,榜单上各国代表团获得的金牌数的众数为( ) 21·世纪*教育网
代表团 挪威 德国 中国 美国 瑞典 荷兰 奥地利
金牌数 16 12 9 8 8 8 7
A.9 B.8.5 C.8 D.7
3.下列统计量中,反映一组数据波动情况的是( )
A.方差 B.众数 C.频率 D.平均数
4.某小组9位同学的中考 ( http: / / www.21cnjy.com )体育测试成绩(满分40分)依次为36,40,39,36,40,38,40,39,40.则这组数据的众数与中位数分别是( )【来源:21·世纪·教育·网】
A.40,39 B.39,40 C.36,40 D.40,40
5.某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较两名同学成绩的( )www-2-1-cnjy-com
A.平均数 B.方差 C.频数分布 D.中位数
6.在对一组样本数据进行分析时,小 ( http: / / www.21cnjy.com )明列出了方差的计算公式: ,由公式提供的信息,判断下列关于样本的说法错误的是( ) 2-1-c-n-j-y
A.平均数是8 B.众数是6 C.中位数是9 D.方差是3.6
7.有一组数据为 , , , ,这组数据的每一个数都减去 后得一组新的数据 , , , ,这两组数据一定不变的是( )
A.中位数 B.众数 C.平均数 D.方差
8.某单位采购了5箱苹果,得到每箱质量各不相同的五个数据.登记入账时将最小的数据又少写了1,则计算结果不受影响的是( ) 21*cnjy*com
A.中位数 B.平均数 C.方差 D.标准差
9.学校为了丰富学生课余活动,开展了一次“爱我中华,唱我中华”的歌咏比赛,共有18名同学人围,他们的决赛成绩如下表: 21·cn·jy·com
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70分,9.60分 B.9.60分,9.60分
C.9.60分,9.70分 D.9.65分,9.60分
10.一城市准备选购一千株高 ( http: / / www.21cnjy.com )度大约为2m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度,得到的数据如下: 【来源:21cnj*y.co*m】
树苗平均高度(单位:m) 标准差
甲苗圃 1.8 0.2
乙苗圃 1.8 0.6
丙苗圃 2.0 0.6
丁苗圃 2.0 0.2
请你帮采购小组出谋划策,应选购( )
A.甲苗圃的树苗 B.乙苗圃的树苗;
C.丙苗圃的树苗 D.丁苗圃的树苗
二、填空题
11.某研究员随机从甲、乙两块试验田中各抽取100株杂交水稻苗测试高度,经测量、计算平均数和方差的结果为 =12cm, =12cm, , ,则杂交水稻长势比较整齐的是 试验田.(填“甲”或“乙”)www.21-cn-jy.com
12.有8个数的平均数是8,另外有12个数的平均数是9,这20个数的平均数是
13.下列五个数:11,12,13,14,15的标准差为
14.现有甲、乙两支排球队,每支球队队员身高的平均数均为1.82米,方差分别为=3.7,=4.2,则身高较整齐的球队是 队.
【出处:21教育名师】
15.某校拟招聘一批优秀教师,其中某位教师 ( http: / / www.21cnjy.com )笔试、试讲、面试三轮测试得分分别为95分、85分、90分,综合成绩笔试、试讲、面试的占比为2:2:1,则该名教师的综合成绩为 .
16.已知一组不全等的数据:x1, ( http: / / www.21cnjy.com )x2,x3,……,xn,平均数是2020,方差是2021,则新数据:2020,x1,x2,x3,……,xn的平均数是 ,方差 2021(填“=、>或<”).
17.为了践行“首都市民卫生健康公约”,某班级举办“七步洗手法”比赛活动,小明的单项成绩如表所示(各项成绩均按百分制计):【版权所有:21教育】
项目 书面测试 实际操作 宣传展示
成绩(分) 96 98 96
若按书面测试占30%、实际操作占50%、宣传展示占20%,计算参赛个人的综合成绩(百分制),则小明的最后得分是 .21教育名师原创作品
18.某村选用条件相同的各6块实验田播种 ( http: / / www.21cnjy.com )甲乙两种水稻良种,结果两种水稻的平均亩产量相同,方差:S2甲=143,S2乙=313,从产量稳定性考虑,适合推广的品种为 .(填“甲”或“乙”)
三、解答题
19.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果 的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示: 21*cnjy*com
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
请计算说明哪位选手成绩更优秀.
20.灯泡厂为测量一批灯泡的寿命,从中随机抽查了50只灯泡,它们的寿命如表所示:
使用寿命 600≤x<1000 1000≤x<1400 1400≤x<1800 1800≤x<2200 2200≤x<2600
灯泡只数 5 10 12 17 6
这批灯泡的平均使用寿命是多少?
21.甲、乙两个小组各6名学生的英语口试测验成绩如下(单位:分).
甲组:76,90,88,82,85,83.
乙组:81,90,91,89,79,74.
请你利用统计知识,说明哪个小组学生的成绩比较稳定.
22.某校八(1)班开展男生、女生垫排球比赛活动,每队各派5名同学参加.下表是男生队和女生队5名同学的比赛数据(单位:个):21教育网
1号 2号 3号 4号 5号
男生队 100 98 110 89 103
女生队 88 100 95 120 97
请回答下列问题:
(1)计算两队的平均成绩;
(2)从成绩稳定性角度考虑,哪队成绩稍好,请说明理由.
23.下图反映了八年级(2)班40名学生在一次数学测验的成绩。
① 从图中观察这个班这次数学测验成绩的中位数和众数。
② 根据图形估计这个班这次数学测验成绩的平均成绩。
( http: / / www.21cnjy.com / )
24.本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.21cnjy.com
( http: / / www.21cnjy.com / )
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组 ( http: / / www.21cnjy.com )对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?2·1·c·n·j·y
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】甲
12.【答案】8.6
13.【答案】
14.【答案】甲
15.【答案】90分
16.【答案】2020;<
17.【答案】97
18.【答案】甲
19.【答案】解:根据题意得:
选手 的综合成绩为: 分,
选手 的综合成绩为: 分
∵
∴选手 的成绩更优秀.
20.【答案】解:平均使用寿命= ,
∴这批灯泡的平均使用寿命是1672.
21.【答案】解:甲组学生成绩的平均数 ;
乙组学生成绩的平均数 ;
甲组成绩的方差
;
乙组成绩的方差
;
,
甲小组学生的成绩比较稳定.
22.【答案】(1)解:男生队: =100(个);
女生队: =100(个).
(2)解: ;
∵ ,
∴男生队的成绩更稳定性,
即男生队成绩稍好.
23.【答案】解:①出现最多的是75分,有8个人,故众数为75(分);
总共有40人的数学成绩,第20、21位都是75分,则中位数为75(分)
②平均数=
估计这个班这次数学测验成绩的平均成绩为71.25.
24.【答案】(1)解:根据题意得:
得4分的学生有50×50%=25(人),
答:得4分的学生有25人
(2)解:根据题意得:
平均分= =3.7(分)
(3)解:设第二次测试中得4分的学生有x人,得5分的学生有y人,根据题意得:
,
解得: ,
答:第二次测试中得4分的学生有15人,得5分的学生有30人
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
