第十八章 平行四边形单元检测卷(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册第十八章平行四边形单元检测卷
一、单选题
1.下列条件中,能判定四边形是平行四边形的条件是( )
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角相等
C.一组对边平行,一组邻角互补
D.一组对边相等,一组邻角相等
2.如图,四边形ABCD中,AB∥ ( http: / / www.21cnjy.com )CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.8 B.9 C.10 D.12
3.如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.8 B.9 C.12 D.15
4.在四边形ABCD中,将下列条件中的任意两个进行组合,可以判定它是平行四边形的有( )组.
(1)AB∥CD(2)AD∥BC(3)AB=CD(4)AD=BC(5)∠A=∠C(6)∠B=∠D
A.7 B.8 C.9 D.10
5.如图,在矩形ABCD中,AB=8,BC=6,顺次连结各边中点得到菱形,再顺次连结菱形各边中点,得到矩形,再顺次连结矩形各边中点,得到菱形,…,这样继续下去.则四边形的面积为( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图所示,正方形ABCD的 ( http: / / www.21cnjy.com )面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则最小值为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.2 B.3 C.4 D.6
7.如图,把含30°的直角三角板PMN放置在正方形ABCD中, ,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则 的度数为( ) 21教育网
( http: / / www.21cnjy.com / )
A.60° B.65° C.75° D.80°
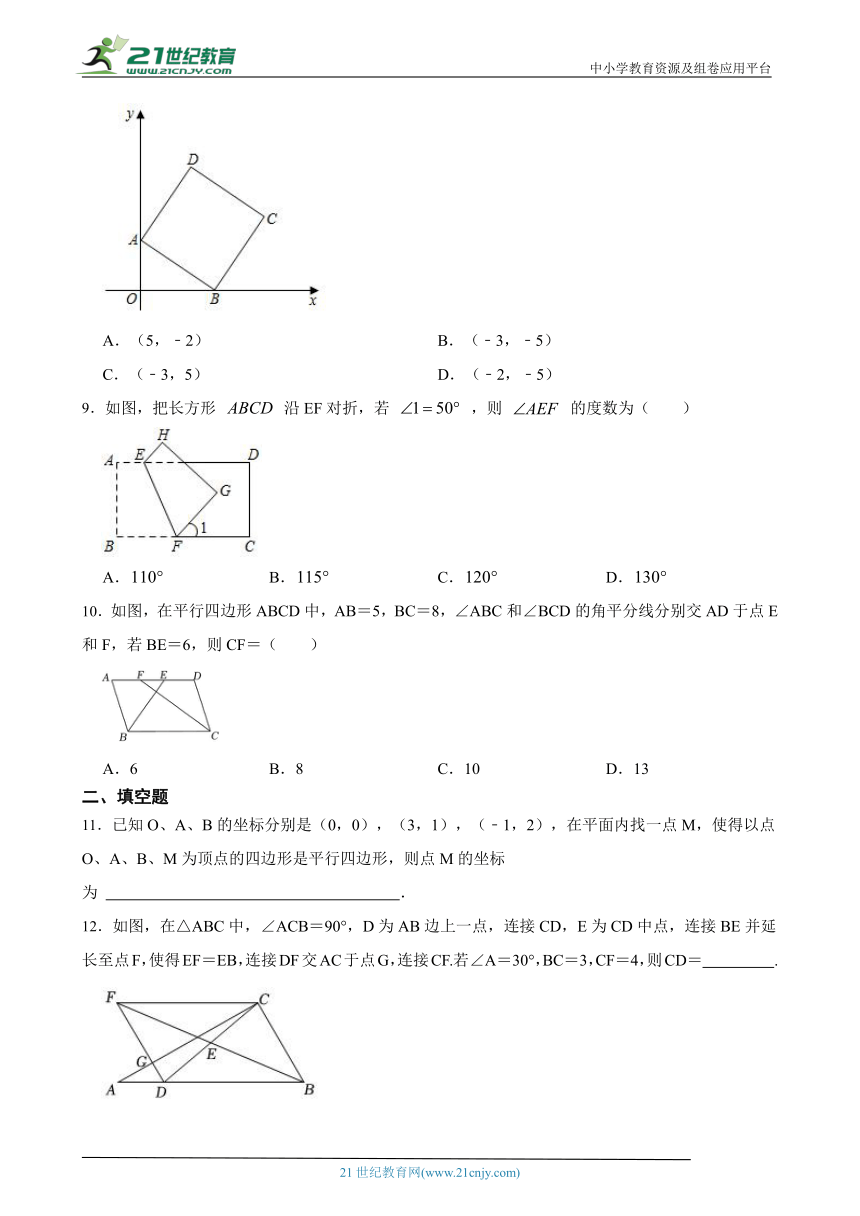
8.如图,在正方形ABCD中,点A(0,2 ( http: / / www.21cnjy.com )),点B(3,0),点C和点D均在第一象限内,将正方形ABCD绕点O逆时针旋转,每秒旋转60°,则第51秒时点D的坐标为( )
( http: / / www.21cnjy.com / )
A.(5,﹣2) B.(﹣3,﹣5)
C.(﹣3,5) D.(﹣2,﹣5)
9.如图,把长方形 沿EF对折,若 ,则 的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )21cnjy.com
A.6 B.8 C.10 D.13
二、填空题
11.已知O、A、B的坐标分别是(0 ( http: / / www.21cnjy.com ),0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .21·世纪*教育网
12.如图,在△ABC中,∠ACB=90° ( http: / / www.21cnjy.com ),D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=3,CF=4,则CD= .
( http: / / www.21cnjy.com / )
13.如图,两条宽都为4cm的纸条交叉成45°角重叠在一起,则重叠四边形的面积为 cm2.
( http: / / www.21cnjy.com / )
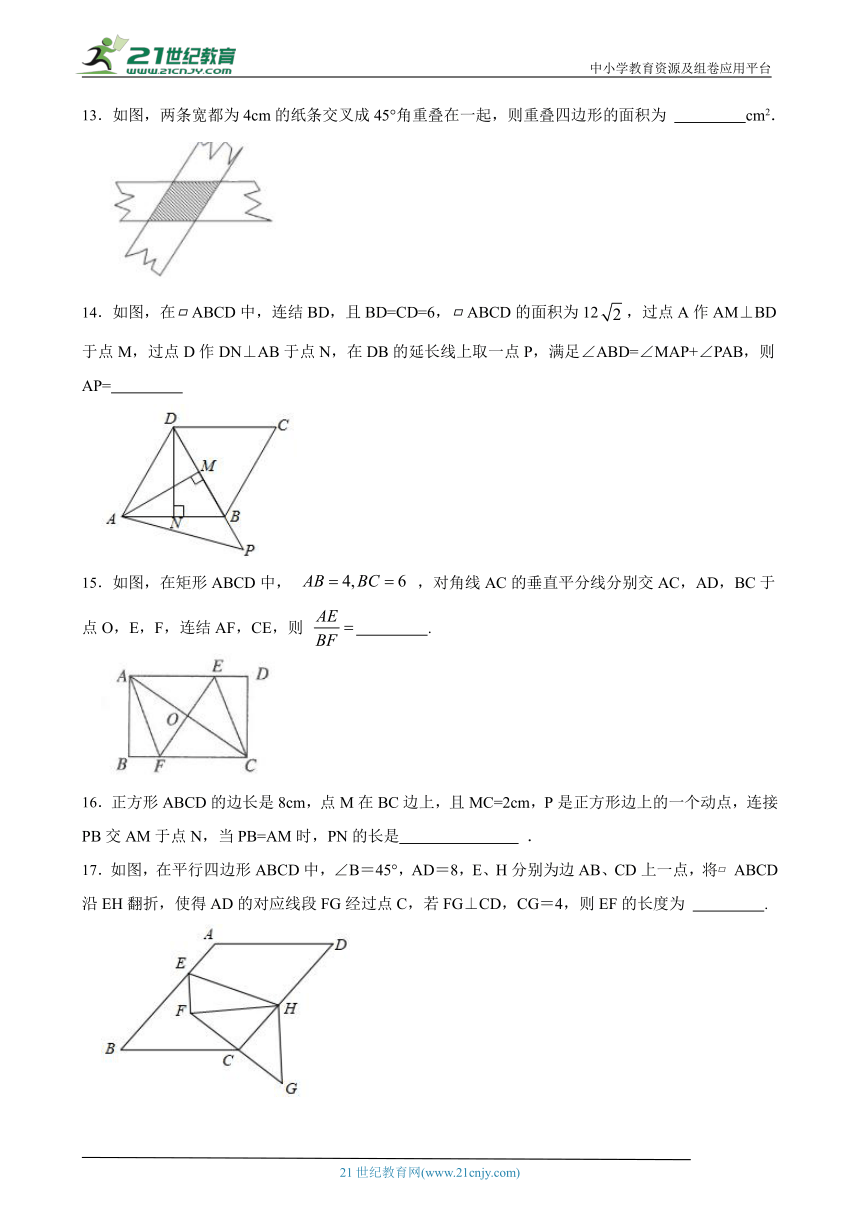
14.如图,在ABCD中,连结BD,且BD=CD=6,ABCD的面积为12,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=
( http: / / www.21cnjy.com / )
15.如图,在矩形ABCD中, ,对角线AC的垂直平分线分别交AC,AD,BC于点O,E,F,连结AF,CE,则 .www.21-cn-jy.com
( http: / / www.21cnjy.com / )
16.正方形ABCD的边长是 ( http: / / www.21cnjy.com )8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB交AM于点N,当PB=AM时,PN的长是 .www-2-1-cnjy-com
17.如图,在平行四边形ABCD中,∠B ( http: / / www.21cnjy.com )=45°,AD=8,E、H分别为边AB、CD上一点,将 ABCD沿EH翻折,使得AD的对应线段FG经过点C,若FG⊥CD,CG=4,则EF的长度为 .
( http: / / www.21cnjy.com / )
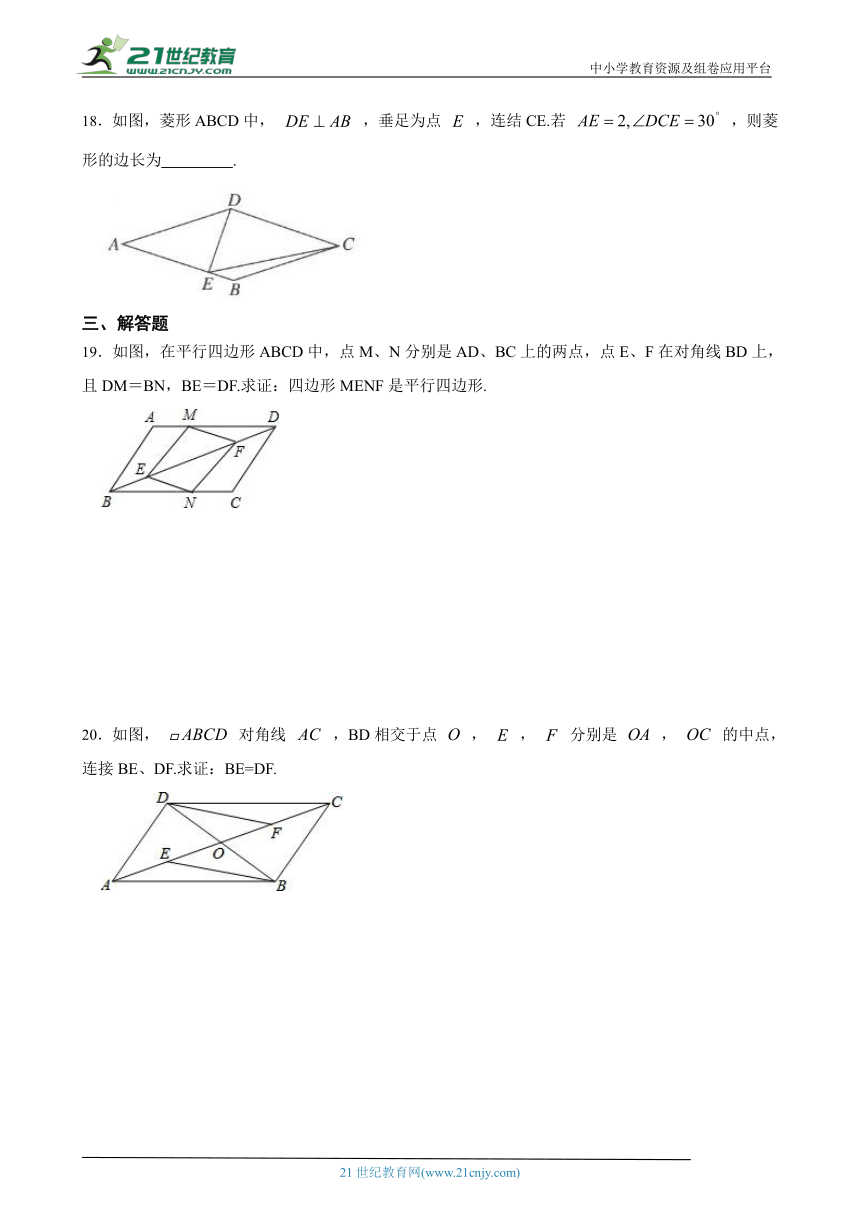
18.如图,菱形ABCD中, ,垂足为点 ,连结CE.若 ,则菱形的边长为 .21*cnjy*com
( http: / / www.21cnjy.com / )
三、解答题
19.如图,在平行四边形 ( http: / / www.21cnjy.com )ABCD中,点M、N分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
20.如图, 对角线 ,BD相交于点 , , 分别是 , 的中点,连接BE、DF.求证:BE=DF. 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
21.如图,矩形ABCD的对角线AC、BD相交于点O,AB=5cm,∠BOC=120°,求矩形对角线的长.
( http: / / www.21cnjy.com / )
22.如图,在矩形中,,,过对角线的交点O作,交于点E,交于点F,求的长.
( http: / / www.21cnjy.com / )
23.如图,在四边形 中, 是 的垂直平分线, 是 上一点, 交 于 ,连接 . ,试证明四边形 是菱形.
( http: / / www.21cnjy.com / )
24.如图,已知 正方形 的面积为 ,求 的面积.
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】(1)C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】(﹣4,1)或(2,3)或(4,﹣1)
12.【答案】
13.【答案】
14.【答案】4
15.【答案】
16.【答案】5cm或5.2cm
17.【答案】
18.【答案】
19.【答案】证明:在平行四边形ABCD中,AD∥BC,
∴∠ADB=∠CBD.
在△BNE和△DMF中,
∴△BNE≌△DMF(SAS).
∴MF=NE,∠DFM=∠BEN.
∴EN∥FM.
∴四边形MENF是平行四边形.
20.【答案】证明:连接BF、DE,如图所示:
( http: / / www.21cnjy.com / )
四边形ABCD是平行四边形,
, ,
、 分别是 、 的中点,
, ,
,
四边形BFDE是平行四边形,
.
21.【答案】解:∵∠BOC=120°,
∴∠AOB=180°﹣120°=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,OA=OC=AC,OB=OD=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=5cm,
∴OA=OB=AB=5cm,
∴AC=2AO=10cm,BD=AC=10cm.
22.【答案】解:连接,
( http: / / www.21cnjy.com / )
∵四边形是矩形,
∴,,,
∵,
∴,
设,则,
∴,
∴,
∴的长为.
23.【答案】证明:∵AC是BD的垂直平分线,
∴
在 和 中
∴ ,
∴ ,
又∵ ,
∴
∴AB∥CD,
∴
又∵
∴
∴
∵
∴
∴四边形ABCD是菱形.
24.【答案】解:∵
∴∠ABC=90°
∵
∴AC=
∵正方形 的面积为 ,
∴正方形 的边长FC=13cm
∵
∴
∴△AFC是直角三角形,
∴ 的面积=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级下册第十八章平行四边形单元检测卷
一、单选题
1.下列条件中,能判定四边形是平行四边形的条件是( )
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角相等
C.一组对边平行,一组邻角互补
D.一组对边相等,一组邻角相等
2.如图,四边形ABCD中,AB∥ ( http: / / www.21cnjy.com )CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A.8 B.9 C.10 D.12
3.如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.8 B.9 C.12 D.15
4.在四边形ABCD中,将下列条件中的任意两个进行组合,可以判定它是平行四边形的有( )组.
(1)AB∥CD(2)AD∥BC(3)AB=CD(4)AD=BC(5)∠A=∠C(6)∠B=∠D
A.7 B.8 C.9 D.10
5.如图,在矩形ABCD中,AB=8,BC=6,顺次连结各边中点得到菱形,再顺次连结菱形各边中点,得到矩形,再顺次连结矩形各边中点,得到菱形,…,这样继续下去.则四边形的面积为( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图所示,正方形ABCD的 ( http: / / www.21cnjy.com )面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则最小值为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.2 B.3 C.4 D.6
7.如图,把含30°的直角三角板PMN放置在正方形ABCD中, ,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则 的度数为( ) 21教育网
( http: / / www.21cnjy.com / )
A.60° B.65° C.75° D.80°
8.如图,在正方形ABCD中,点A(0,2 ( http: / / www.21cnjy.com )),点B(3,0),点C和点D均在第一象限内,将正方形ABCD绕点O逆时针旋转,每秒旋转60°,则第51秒时点D的坐标为( )
( http: / / www.21cnjy.com / )
A.(5,﹣2) B.(﹣3,﹣5)
C.(﹣3,5) D.(﹣2,﹣5)
9.如图,把长方形 沿EF对折,若 ,则 的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )21cnjy.com
A.6 B.8 C.10 D.13
二、填空题
11.已知O、A、B的坐标分别是(0 ( http: / / www.21cnjy.com ),0),(3,1),(﹣1,2),在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为 .21·世纪*教育网
12.如图,在△ABC中,∠ACB=90° ( http: / / www.21cnjy.com ),D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=3,CF=4,则CD= .
( http: / / www.21cnjy.com / )
13.如图,两条宽都为4cm的纸条交叉成45°角重叠在一起,则重叠四边形的面积为 cm2.
( http: / / www.21cnjy.com / )
14.如图,在ABCD中,连结BD,且BD=CD=6,ABCD的面积为12,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=
( http: / / www.21cnjy.com / )
15.如图,在矩形ABCD中, ,对角线AC的垂直平分线分别交AC,AD,BC于点O,E,F,连结AF,CE,则 .www.21-cn-jy.com
( http: / / www.21cnjy.com / )
16.正方形ABCD的边长是 ( http: / / www.21cnjy.com )8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB交AM于点N,当PB=AM时,PN的长是 .www-2-1-cnjy-com
17.如图,在平行四边形ABCD中,∠B ( http: / / www.21cnjy.com )=45°,AD=8,E、H分别为边AB、CD上一点,将 ABCD沿EH翻折,使得AD的对应线段FG经过点C,若FG⊥CD,CG=4,则EF的长度为 .
( http: / / www.21cnjy.com / )
18.如图,菱形ABCD中, ,垂足为点 ,连结CE.若 ,则菱形的边长为 .21*cnjy*com
( http: / / www.21cnjy.com / )
三、解答题
19.如图,在平行四边形 ( http: / / www.21cnjy.com )ABCD中,点M、N分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
20.如图, 对角线 ,BD相交于点 , , 分别是 , 的中点,连接BE、DF.求证:BE=DF. 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
21.如图,矩形ABCD的对角线AC、BD相交于点O,AB=5cm,∠BOC=120°,求矩形对角线的长.
( http: / / www.21cnjy.com / )
22.如图,在矩形中,,,过对角线的交点O作,交于点E,交于点F,求的长.
( http: / / www.21cnjy.com / )
23.如图,在四边形 中, 是 的垂直平分线, 是 上一点, 交 于 ,连接 . ,试证明四边形 是菱形.
( http: / / www.21cnjy.com / )
24.如图,已知 正方形 的面积为 ,求 的面积.
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】(1)C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】(﹣4,1)或(2,3)或(4,﹣1)
12.【答案】
13.【答案】
14.【答案】4
15.【答案】
16.【答案】5cm或5.2cm
17.【答案】
18.【答案】
19.【答案】证明:在平行四边形ABCD中,AD∥BC,
∴∠ADB=∠CBD.
在△BNE和△DMF中,
∴△BNE≌△DMF(SAS).
∴MF=NE,∠DFM=∠BEN.
∴EN∥FM.
∴四边形MENF是平行四边形.
20.【答案】证明:连接BF、DE,如图所示:
( http: / / www.21cnjy.com / )
四边形ABCD是平行四边形,
, ,
、 分别是 、 的中点,
, ,
,
四边形BFDE是平行四边形,
.
21.【答案】解:∵∠BOC=120°,
∴∠AOB=180°﹣120°=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,OA=OC=AC,OB=OD=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=5cm,
∴OA=OB=AB=5cm,
∴AC=2AO=10cm,BD=AC=10cm.
22.【答案】解:连接,
( http: / / www.21cnjy.com / )
∵四边形是矩形,
∴,,,
∵,
∴,
设,则,
∴,
∴,
∴的长为.
23.【答案】证明:∵AC是BD的垂直平分线,
∴
在 和 中
∴ ,
∴ ,
又∵ ,
∴
∴AB∥CD,
∴
又∵
∴
∴
∵
∴
∴四边形ABCD是菱形.
24.【答案】解:∵
∴∠ABC=90°
∵
∴AC=
∵正方形 的面积为 ,
∴正方形 的边长FC=13cm
∵
∴
∴△AFC是直角三角形,
∴ 的面积=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
