27.1 图形的相似同步练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册27.1图形的相似章节小测
一、单选题
1.下列说法正确的是( )
A.正五边形都相似 B.等腰三角形都相似
C.直角三角形都相似 D.钝角三角形都相似
2.在我们日常生活中存在很多较小的或 ( http: / / www.21cnjy.com )眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )
( http: / / www.21cnjy.com / )
A.平移变换 B.旋转变换 C.轴对称变换 D.相似变换
3.下列两个图形一定相似的是( )
A.两个菱形 B.两个周长相等的直角三角形
C.两个正方形 D.两个等腰梯形
4.如图,平行于正多边形一边的直线,正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( ) 21cnjy.com
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
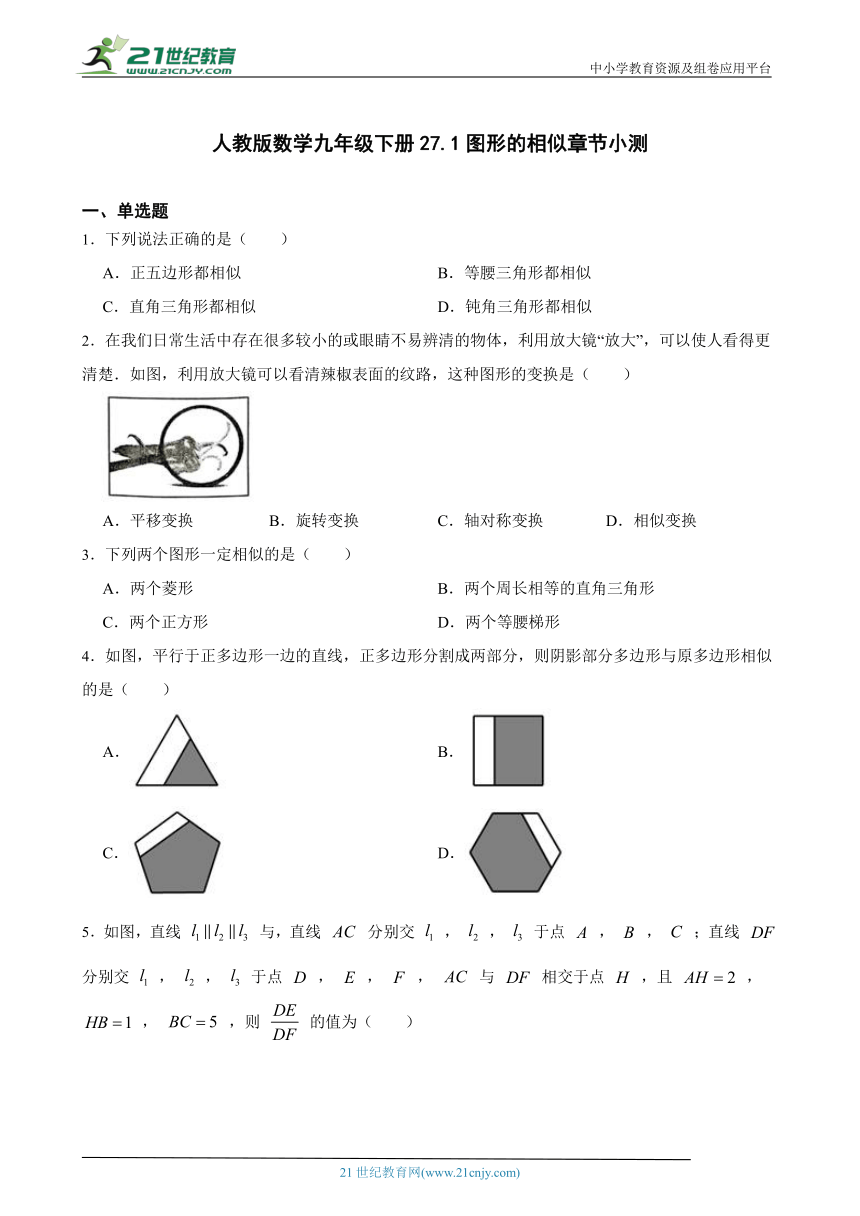
5.如图,直线 与,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( ) www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图,将- -张矩形纸片 ( http: / / www.21cnjy.com )沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( ) 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
7.下面关于两个图形相似的判断:①两个等腰三 ( http: / / www.21cnjy.com )角形相似;②两个等边三角形相似;③两个等腰直角三角形相似;④两个正方形相似;⑤两个等腰梯形相似.其中正确的个数是( )
A.1 B.2 C.3 D.4
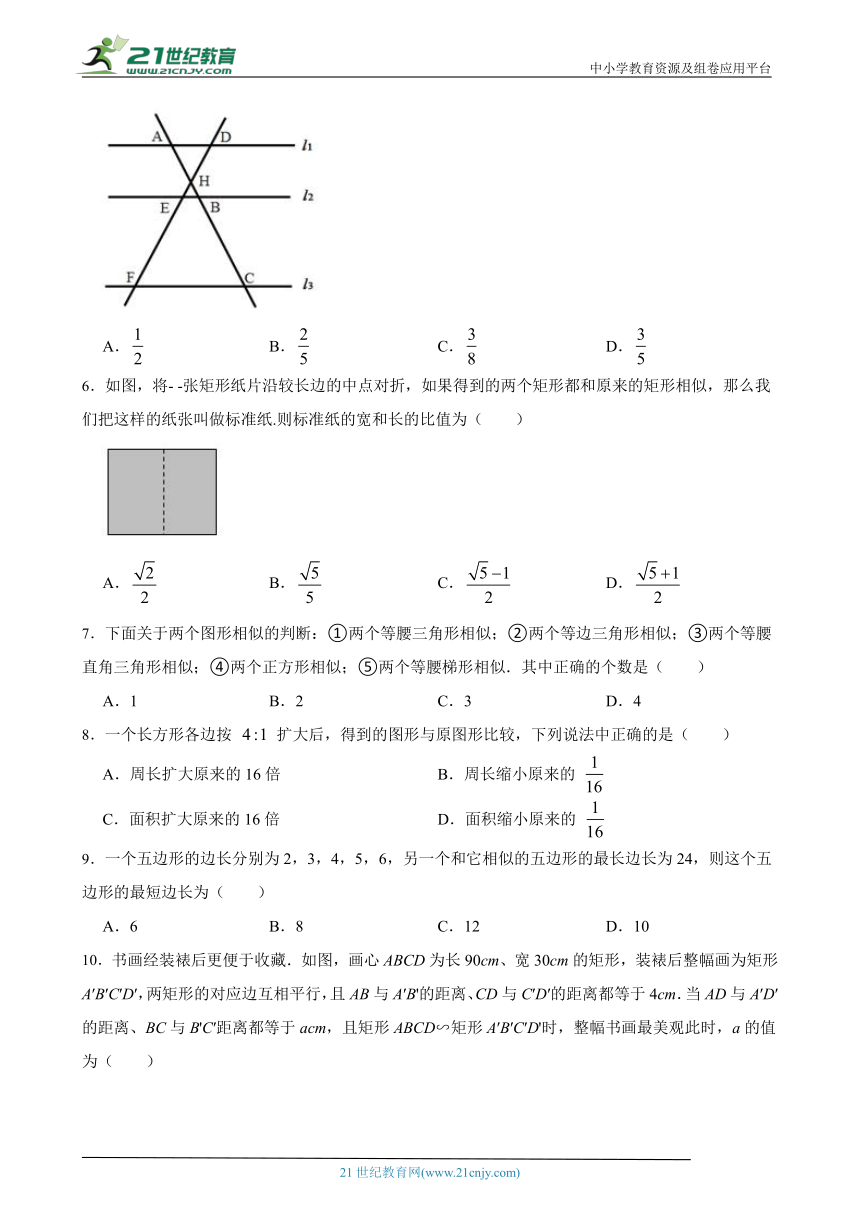
8.一个长方形各边按 扩大后,得到的图形与原图形比较,下列说法中正确的是( )
A.周长扩大原来的16倍 B.周长缩小原来的
C.面积扩大原来的16倍 D.面积缩小原来的
9.一个五边形的边长分别为2,3,4,5,6,另一个和它相似的五边形的最长边长为24,则这个五边形的最短边长为( )21*cnjy*com
A.6 B.8 C.12 D.10
10.书画经装裱后更便于收藏.如图,画心A ( http: / / www.21cnjy.com )BCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm.当AD与A′D′的距离、BC与B'C′距离都等于acm,且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( ) 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
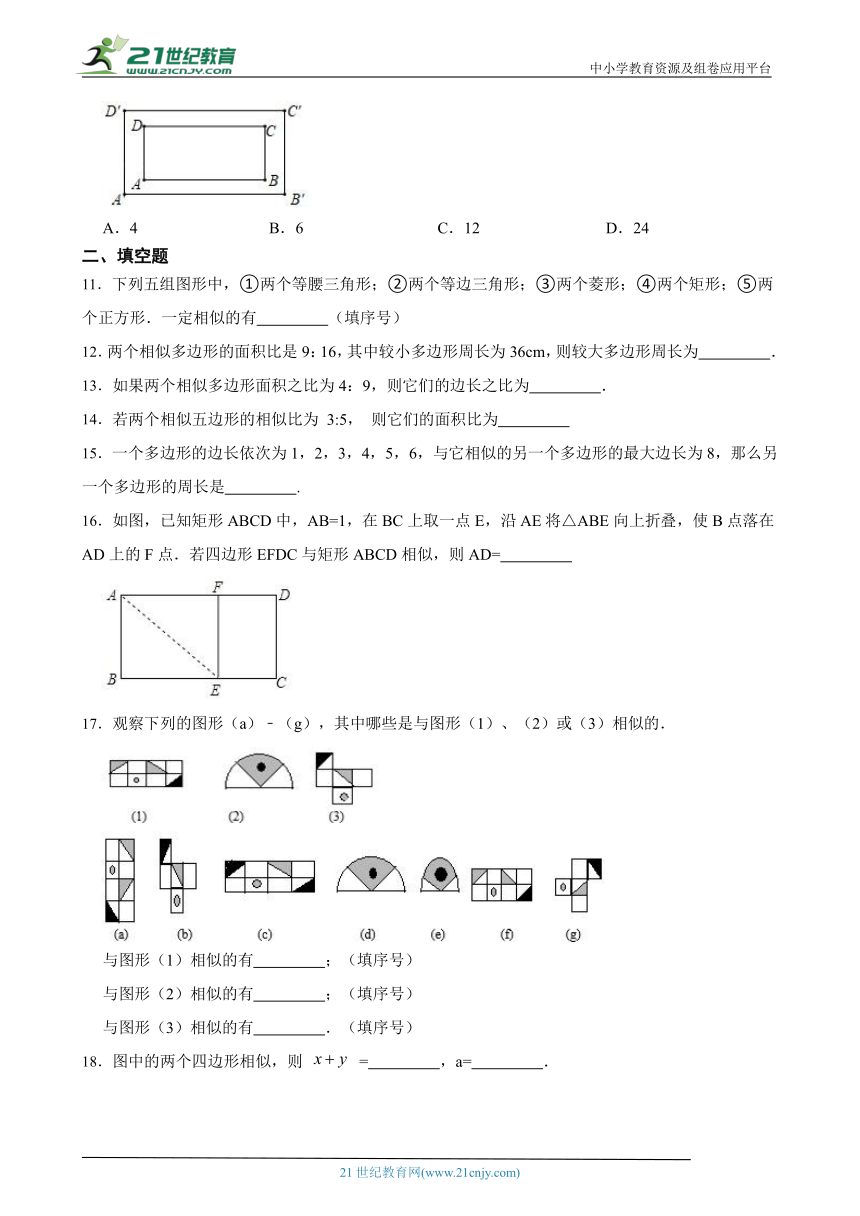
A.4 B.6 C.12 D.24
二、填空题
11.下列五组图形中,①两个等腰三角形;②两个等边三角形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有 (填序号)21·cn·jy·com
12.两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为 .
13.如果两个相似多边形面积之比为4:9,则它们的边长之比为 .
14.若两个相似五边形的相似比为 3:5, 则它们的面积比为
15.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是 . 【出处:21教育名师】
16.如图,已知矩形ABCD中, ( http: / / www.21cnjy.com )AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= 【版权所有:21教育】
( http: / / www.21cnjy.com / )
17.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
与图形(1)相似的有 ;(填序号)
与图形(2)相似的有 ;(填序号)
与图形(3)相似的有 .(填序号)
18.图中的两个四边形相似,则 = ,a= .
( http: / / www.21cnjy.com / )
三、综合题
19.如图,四边形ABCD∽四边形A'B'C'D'.
( http: / / www.21cnjy.com / )
(1)α= ,它们的相似比是 .
(2)求边x、y的长度.
20.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:【来源:21·世纪·教育·网】
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
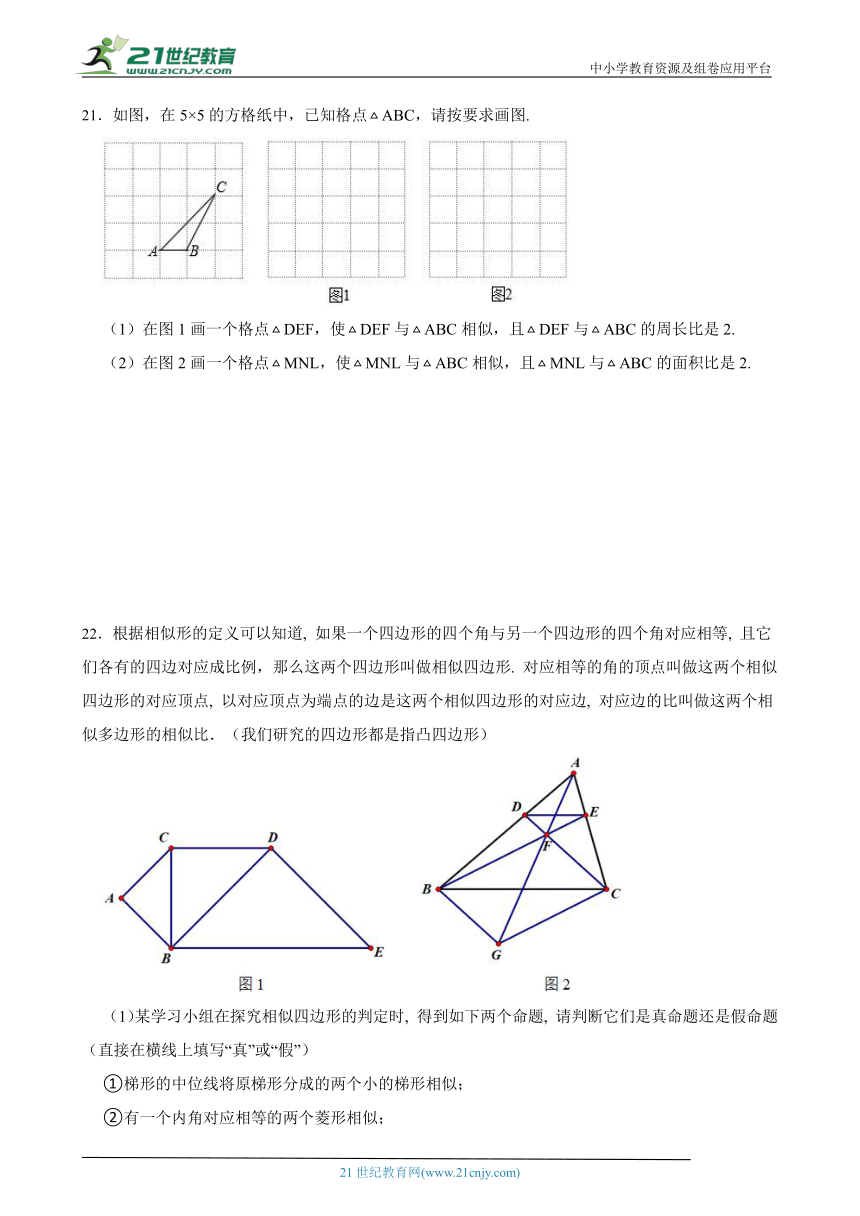
21.如图,在5×5的方格纸中,已知格点ABC,请按要求画图.
( http: / / www.21cnjy.com / )
(1)在图1画一个格点DEF,使DEF与ABC相似,且DEF与ABC的周长比是2.
(2)在图2画一个格点MNL,使MNL与ABC相似,且MNL与ABC的面积比是2.
22.根据相似形的定义可以 ( http: / / www.21cnjy.com )知道, 如果一个四边形的四个角与另一个四边形的四个角对应相等, 且它们各有的四边对应成比例,那么这两个四边形叫做相似四边形. 对应相等的角的顶点叫做这两个相似四边形的对应顶点, 以对应顶点为端点的边是这两个相似四边形的对应边, 对应边的比叫做这两个相似多边形的相似比.(我们研究的四边形都是指凸四边形)www.21-cn-jy.com
( http: / / www.21cnjy.com / )
(1)某学习小组在探究相似四边形的判定时, 得到如下两个命题, 请判断它们是真命题还是假命题(直接在横线上填写“真”或“假”)2·1·c·n·j·y
①梯形的中位线将原梯形分成的两个小的梯形相似;
②有一个内角对应相等的两个菱形相似;
(2)已知:如图1, 是以 为斜边的等腰直角三角形, 以 为直角边作等腰直角三角形,再以为直角边作等腰直角三角形.21·世纪*教育网
求证:四边形 与四边形 相似.
(3)已知:如图2,在中,点分别在边上,相交于点F,点在的延长线上,联结如果四边形与四边形相似,且点分别对应.21世纪教育网版权所有
求证:.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】C
11.【答案】②⑤
12.【答案】48cm
13.【答案】2:3
14.【答案】9:25
15.【答案】28
16.【答案】
17.【答案】a;d;g
18.【答案】63;85°
19.【答案】(1)83°;
(2)解:∵四边形ABCD∽四边形A'B'C'D',
∴ ,
解得,x=12,y= .
20.【答案】(1)解:设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)解:不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
21.【答案】(1)解:如图所示:
( http: / / www.21cnjy.com / )
,,,,,
∴,
∴△DEF∽△ABC,
∴△DEF与△ABC的周长比是2;
(2)解:如图所示,
( http: / / www.21cnjy.com / )
,,,,,,
∴,
∴△MNL∽△ABC,
∴△MNL与△ABC的面积比是2.
22.【答案】(1)解:①梯形的中位线 ( http: / / www.21cnjy.com )将原梯形分成的两个小的梯形,两个小梯形的四个角相等,并且其对应的腰相等,但是两个小梯形的上底不相等,故对应边不成比例,因此是假命题
②有一个内角对应相等的两个菱形相似,有一个内角的相等的两个菱形的四个角相等,并且菱形四条边相等,故对应的边之比相等,因此是真命题21教育网
(2)证明:由题意可知:、、是等腰直角三角形,
,,
,,,
故有,,
设,
在,由勾股定理可知:,
在中,由勾股定理可知:,
在中,由勾股定理可知:,
在四边形 与四边形 中,,,,,且,
四边形 与四边形 相似.
(3)证明:四边形与四边形相似,
,,
在与中,,,
,
,
在与中,,,
,
,,
,
,
在与中,,,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册27.1图形的相似章节小测
一、单选题
1.下列说法正确的是( )
A.正五边形都相似 B.等腰三角形都相似
C.直角三角形都相似 D.钝角三角形都相似
2.在我们日常生活中存在很多较小的或 ( http: / / www.21cnjy.com )眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )
( http: / / www.21cnjy.com / )
A.平移变换 B.旋转变换 C.轴对称变换 D.相似变换
3.下列两个图形一定相似的是( )
A.两个菱形 B.两个周长相等的直角三角形
C.两个正方形 D.两个等腰梯形
4.如图,平行于正多边形一边的直线,正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( ) 21cnjy.com
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
5.如图,直线 与,直线 分别交 , , 于点 , , ;直线 分别交 , , 于点 , , , 与 相交于点 ,且 , , ,则 的值为( ) www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图,将- -张矩形纸片 ( http: / / www.21cnjy.com )沿较长边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么我们把这样的纸张叫做标准纸.则标准纸的宽和长的比值为( ) 2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
7.下面关于两个图形相似的判断:①两个等腰三 ( http: / / www.21cnjy.com )角形相似;②两个等边三角形相似;③两个等腰直角三角形相似;④两个正方形相似;⑤两个等腰梯形相似.其中正确的个数是( )
A.1 B.2 C.3 D.4
8.一个长方形各边按 扩大后,得到的图形与原图形比较,下列说法中正确的是( )
A.周长扩大原来的16倍 B.周长缩小原来的
C.面积扩大原来的16倍 D.面积缩小原来的
9.一个五边形的边长分别为2,3,4,5,6,另一个和它相似的五边形的最长边长为24,则这个五边形的最短边长为( )21*cnjy*com
A.6 B.8 C.12 D.10
10.书画经装裱后更便于收藏.如图,画心A ( http: / / www.21cnjy.com )BCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm.当AD与A′D′的距离、BC与B'C′距离都等于acm,且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( ) 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.4 B.6 C.12 D.24
二、填空题
11.下列五组图形中,①两个等腰三角形;②两个等边三角形;③两个菱形;④两个矩形;⑤两个正方形.一定相似的有 (填序号)21·cn·jy·com
12.两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为 .
13.如果两个相似多边形面积之比为4:9,则它们的边长之比为 .
14.若两个相似五边形的相似比为 3:5, 则它们的面积比为
15.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是 . 【出处:21教育名师】
16.如图,已知矩形ABCD中, ( http: / / www.21cnjy.com )AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= 【版权所有:21教育】
( http: / / www.21cnjy.com / )
17.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
与图形(1)相似的有 ;(填序号)
与图形(2)相似的有 ;(填序号)
与图形(3)相似的有 .(填序号)
18.图中的两个四边形相似,则 = ,a= .
( http: / / www.21cnjy.com / )
三、综合题
19.如图,四边形ABCD∽四边形A'B'C'D'.
( http: / / www.21cnjy.com / )
(1)α= ,它们的相似比是 .
(2)求边x、y的长度.
20.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:【来源:21·世纪·教育·网】
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
21.如图,在5×5的方格纸中,已知格点ABC,请按要求画图.
( http: / / www.21cnjy.com / )
(1)在图1画一个格点DEF,使DEF与ABC相似,且DEF与ABC的周长比是2.
(2)在图2画一个格点MNL,使MNL与ABC相似,且MNL与ABC的面积比是2.
22.根据相似形的定义可以 ( http: / / www.21cnjy.com )知道, 如果一个四边形的四个角与另一个四边形的四个角对应相等, 且它们各有的四边对应成比例,那么这两个四边形叫做相似四边形. 对应相等的角的顶点叫做这两个相似四边形的对应顶点, 以对应顶点为端点的边是这两个相似四边形的对应边, 对应边的比叫做这两个相似多边形的相似比.(我们研究的四边形都是指凸四边形)www.21-cn-jy.com
( http: / / www.21cnjy.com / )
(1)某学习小组在探究相似四边形的判定时, 得到如下两个命题, 请判断它们是真命题还是假命题(直接在横线上填写“真”或“假”)2·1·c·n·j·y
①梯形的中位线将原梯形分成的两个小的梯形相似;
②有一个内角对应相等的两个菱形相似;
(2)已知:如图1, 是以 为斜边的等腰直角三角形, 以 为直角边作等腰直角三角形,再以为直角边作等腰直角三角形.21·世纪*教育网
求证:四边形 与四边形 相似.
(3)已知:如图2,在中,点分别在边上,相交于点F,点在的延长线上,联结如果四边形与四边形相似,且点分别对应.21世纪教育网版权所有
求证:.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】C
11.【答案】②⑤
12.【答案】48cm
13.【答案】2:3
14.【答案】9:25
15.【答案】28
16.【答案】
17.【答案】a;d;g
18.【答案】63;85°
19.【答案】(1)83°;
(2)解:∵四边形ABCD∽四边形A'B'C'D',
∴ ,
解得,x=12,y= .
20.【答案】(1)解:设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)解:不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
21.【答案】(1)解:如图所示:
( http: / / www.21cnjy.com / )
,,,,,
∴,
∴△DEF∽△ABC,
∴△DEF与△ABC的周长比是2;
(2)解:如图所示,
( http: / / www.21cnjy.com / )
,,,,,,
∴,
∴△MNL∽△ABC,
∴△MNL与△ABC的面积比是2.
22.【答案】(1)解:①梯形的中位线 ( http: / / www.21cnjy.com )将原梯形分成的两个小的梯形,两个小梯形的四个角相等,并且其对应的腰相等,但是两个小梯形的上底不相等,故对应边不成比例,因此是假命题
②有一个内角对应相等的两个菱形相似,有一个内角的相等的两个菱形的四个角相等,并且菱形四条边相等,故对应的边之比相等,因此是真命题21教育网
(2)证明:由题意可知:、、是等腰直角三角形,
,,
,,,
故有,,
设,
在,由勾股定理可知:,
在中,由勾股定理可知:,
在中,由勾股定理可知:,
在四边形 与四边形 中,,,,,且,
四边形 与四边形 相似.
(3)证明:四边形与四边形相似,
,,
在与中,,,
,
,
在与中,,,
,
,,
,
,
在与中,,,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
