27.2 相似三角形同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册27.2相似三角形小测
一、单选题
1.如图,在△ABC中,点D在边AB上,若∠ACD=∠B,AD=3,BD=4,则AC的长为( )
( http: / / www.21cnjy.com / )
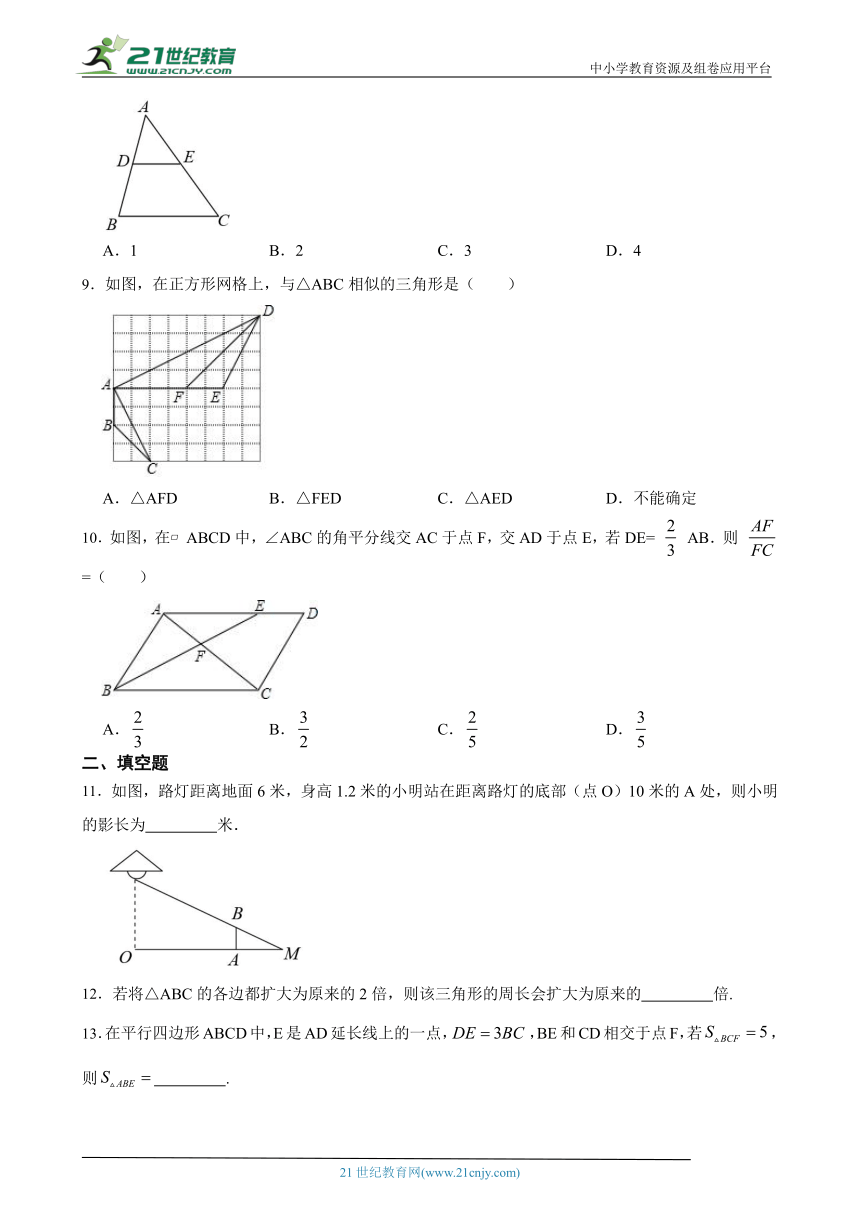
A.2 B. C.5 D.2
2.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,并测得,,那么树DB的高度是( )21cnjy.com
( http: / / www.21cnjy.com / )
A.6m B.8m C.32m D.25m
3.如图,在△ABC中,点D,E分别在边AB,AC上,且 = = ,则△ADE周长与△ABC的周长比是( ) www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.1: B.1:2 C.1:3 D.1:4
4.如图,点P是△ABC的AC边上一点,连接BP,添加下列条件,不能判定△ABC∽△APB的是( )
( http: / / www.21cnjy.com / )
A.∠C=∠ABP B.∠ABC=∠APB
C.= D.=
5.如图,在菱形中,点分别是边的中点,连接.若菱形的面积为8,则的面积为( )
( http: / / www.21cnjy.com / )
A.2 B.3 C.4 D.5
6.如图,直线l1∥l2,直线AB、CD相交于点E,若AE=4,BE=8,CD=9,则线段CE的长为( )
( http: / / www.21cnjy.com / )
A.3 B.5 C.7 D.9
7.根据下列条件,判断△ABC与△A′B′C′能相似的条件有( )
①∠C=∠C′=90°,∠A=25°,∠B′=65°;
②∠C=90°,AC=6cm,BC=4cm,,A′C′=9cm,B′C′=6cm;
③AB=10cm,BC=12cm,AC=15cm,A′B′=150cm,B′C′=180cm,A′C′=225cm;
④△ABC与△A′B′C′是有一个角为80°等腰三角形
A.1对 B.2对 C.3对 D.4对
8.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的面积是1,则四边形BCED的面积是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
9.如图,在正方形网格上,与△ABC相似的三角形是( )
( http: / / www.21cnjy.com / )
A.△AFD B.△FED C.△AED D.不能确定
10.如图,在 ABCD中,∠ABC的角平分线交AC于点F,交AD于点E,若DE= AB.则 =( ) 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
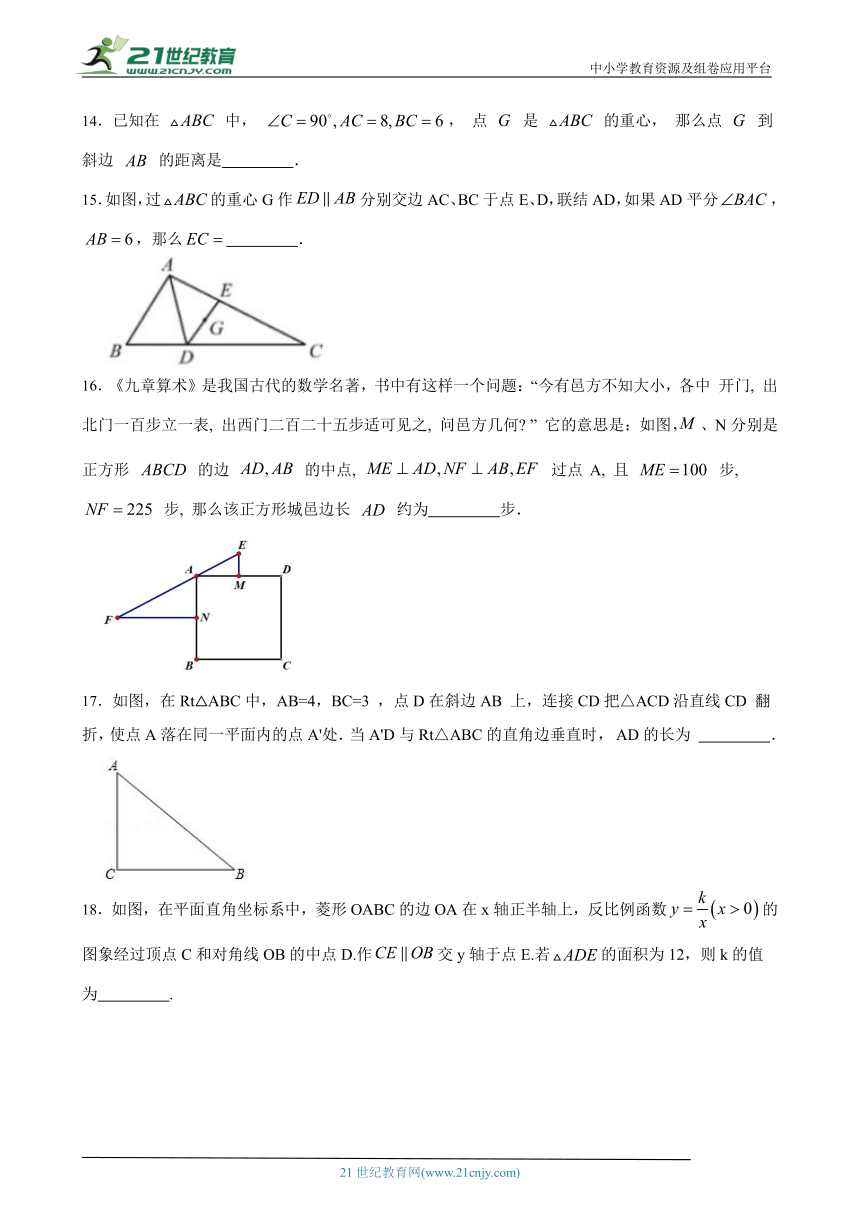
11.如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为 米.21·世纪*教育网
( http: / / www.21cnjy.com / )
12.若将△ABC的各边都扩大为原来的2倍,则该三角形的周长会扩大为原来的 倍.
13.在平行四边形ABCD中,E是AD延长线上的一点,,BE和CD相交于点F,若,则 .www-2-1-cnjy-com
14.已知在 中, , 点 是 的重心, 那么点 到斜边 的距离是 .21教育网
15.如图,过的重心G作分别交边AC、BC于点E、D,联结AD,如果AD平分,,那么 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
16.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中 开门, 出北门一百步立一表, 出西门二百二十五步适可见之, 问邑方几何 ” 它的意思是:如图、N分别是正方形 的边 的中点, 过点 A, 且 步, 步, 那么该正方形城邑边长 约为 步.21*cnjy*com
( http: / / www.21cnjy.com / )
17.如图,在Rt△ABC中 ( http: / / www.21cnjy.com ),AB=4,BC=3 ,点D在斜边AB 上,连接CD把△ACD沿直线CD 翻折,使点A落在同一平面内的点A'处.当A'D与Rt△ABC的直角边垂直时, AD的长为 .
( http: / / www.21cnjy.com / )
18.如图,在平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,反比例函数的图象经过顶点C和对角线OB的中点D.作交y轴于点E.若的面积为12,则k的值为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
三、解答题
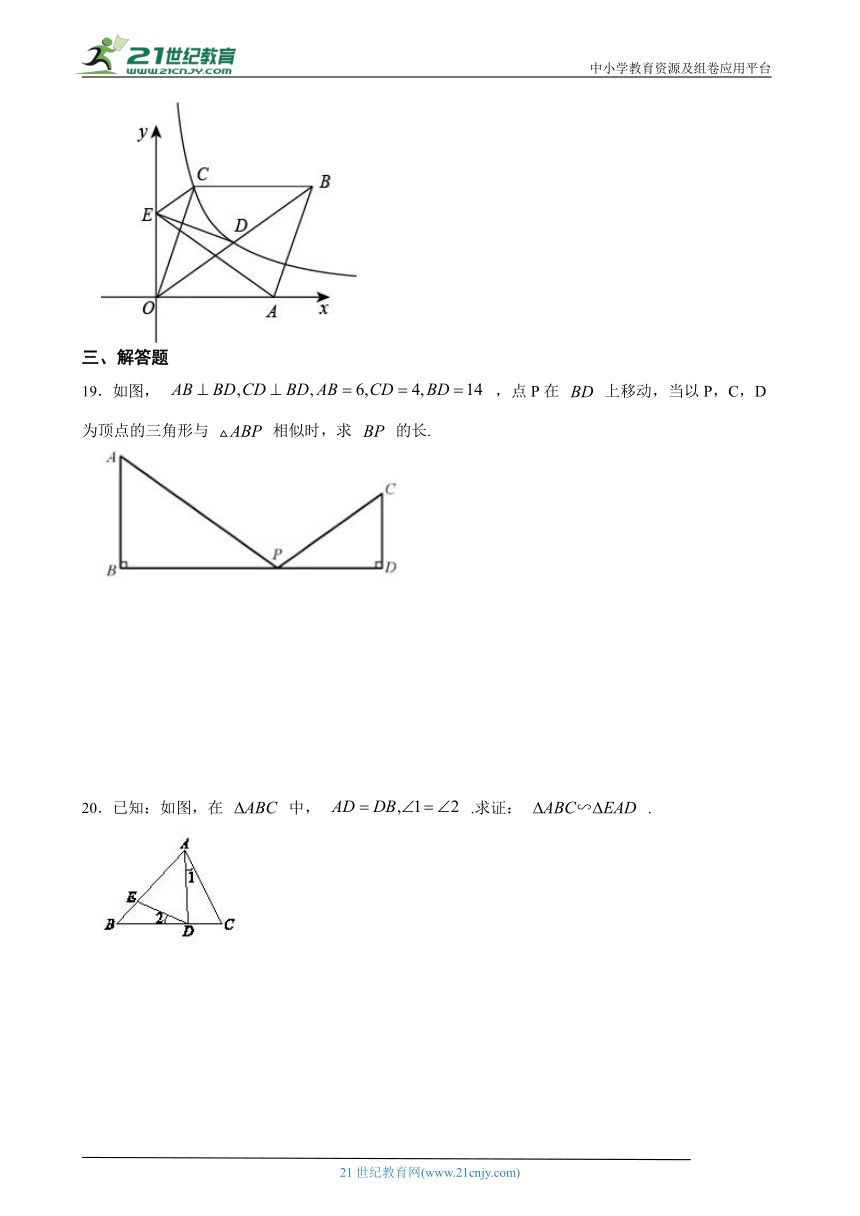
19.如图, ,点P在 上移动,当以P,C,D为顶点的三角形与 相似时,求 的长. 【出处:21教育名师】
( http: / / www.21cnjy.com / )
20.已知:如图,在 中, .求证: .
( http: / / www.21cnjy.com / )
21.如图,Rt△ABC中,∠A ( http: / / www.21cnjy.com )CB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?21世纪教育网版权所有
( http: / / www.21cnjy.com / )
22.如图,点D在 的内部, , , , ,求AD的长.
( http: / / www.21cnjy.com / )
23.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长21·cn·jy·com
( http: / / www.21cnjy.com / )
24.如图,小明同学为了测量教学楼的高度 ,先在操场上点A处放一面镜子,从点A处后退 到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动 放在C处,从点C处向后退 点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度 , 为 ,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度 .
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】D
11.【答案】2.5
12.【答案】2
13.【答案】80
14.【答案】
15.【答案】8
16.【答案】300
17.【答案】1或
18.【答案】32
19.【答案】解:设DP=x,则BP=BD-x=14-x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当 时,△ABP∽△CDP,即 ,
解得 ;
当 时,△ABP∽△PDC,即 ,
整理得x2-14x+24=0,
解得x1=2,x2=12,
BP=14-2=12,BP=14-12=2,
∴当BP为8.4或2或12时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
20.【答案】证明:∵ ,
∴ .
∵ , 且 ,
∴ ,
∴ .
21.【答案】解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm,
分两种情况:
①当∠EDB=∠ACB=90°时,
DE∥AC,△EBD∽△ABC,
∵D为BC的中点,
∴BD=CD= BC=1cm,E为AB的中点,AE=BE= AB=2cm,
∴t=2s;
②当∠DEB=∠ACB=90°时,
∵∠B=∠B,
∴△DBE∽△ABC,
∴∠BDE=∠A=30°,
∴BE= BD=cm,
∴AE=3.5cm,
∴t=3.5s;
综上所述:当以B、D、E为顶点的三角形与△ABC相似时,t的值为2或3.5;
22.【答案】解:延长AD,如图所示
. ( http: / / www.21cnjy.com / )
∵∠1+∠BAC=180°,∠1+∠BDE=180°,
∴∠BAC=∠BDE.
又∵∠BAC=∠BAD+∠CAD,∠BDE=∠BAD+∠B,
∴∠B=∠CAD.
∵∠1=∠2,
∴△ABD∽△CAD,
∴ ,即 ,
∴ .
23.【答案】解::∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴
∴ ,
∴AD=4.
24.【答案】解:由已知得, , , ,
, ,
( http: / / www.21cnjy.com / )
∴在 和 中
∴
∴ ,即 ,
∴ ,
在 和 中
∴
∴ ,即 ,
∴
∴ ,
∴
∴ ,
答:教学楼的高度 为 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册27.2相似三角形小测
一、单选题
1.如图,在△ABC中,点D在边AB上,若∠ACD=∠B,AD=3,BD=4,则AC的长为( )
( http: / / www.21cnjy.com / )
A.2 B. C.5 D.2
2.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,并测得,,那么树DB的高度是( )21cnjy.com
( http: / / www.21cnjy.com / )
A.6m B.8m C.32m D.25m
3.如图,在△ABC中,点D,E分别在边AB,AC上,且 = = ,则△ADE周长与△ABC的周长比是( ) www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.1: B.1:2 C.1:3 D.1:4
4.如图,点P是△ABC的AC边上一点,连接BP,添加下列条件,不能判定△ABC∽△APB的是( )
( http: / / www.21cnjy.com / )
A.∠C=∠ABP B.∠ABC=∠APB
C.= D.=
5.如图,在菱形中,点分别是边的中点,连接.若菱形的面积为8,则的面积为( )
( http: / / www.21cnjy.com / )
A.2 B.3 C.4 D.5
6.如图,直线l1∥l2,直线AB、CD相交于点E,若AE=4,BE=8,CD=9,则线段CE的长为( )
( http: / / www.21cnjy.com / )
A.3 B.5 C.7 D.9
7.根据下列条件,判断△ABC与△A′B′C′能相似的条件有( )
①∠C=∠C′=90°,∠A=25°,∠B′=65°;
②∠C=90°,AC=6cm,BC=4cm,,A′C′=9cm,B′C′=6cm;
③AB=10cm,BC=12cm,AC=15cm,A′B′=150cm,B′C′=180cm,A′C′=225cm;
④△ABC与△A′B′C′是有一个角为80°等腰三角形
A.1对 B.2对 C.3对 D.4对
8.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的面积是1,则四边形BCED的面积是( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.1 B.2 C.3 D.4
9.如图,在正方形网格上,与△ABC相似的三角形是( )
( http: / / www.21cnjy.com / )
A.△AFD B.△FED C.△AED D.不能确定
10.如图,在 ABCD中,∠ABC的角平分线交AC于点F,交AD于点E,若DE= AB.则 =( ) 2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
11.如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为 米.21·世纪*教育网
( http: / / www.21cnjy.com / )
12.若将△ABC的各边都扩大为原来的2倍,则该三角形的周长会扩大为原来的 倍.
13.在平行四边形ABCD中,E是AD延长线上的一点,,BE和CD相交于点F,若,则 .www-2-1-cnjy-com
14.已知在 中, , 点 是 的重心, 那么点 到斜边 的距离是 .21教育网
15.如图,过的重心G作分别交边AC、BC于点E、D,联结AD,如果AD平分,,那么 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
16.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中 开门, 出北门一百步立一表, 出西门二百二十五步适可见之, 问邑方几何 ” 它的意思是:如图、N分别是正方形 的边 的中点, 过点 A, 且 步, 步, 那么该正方形城邑边长 约为 步.21*cnjy*com
( http: / / www.21cnjy.com / )
17.如图,在Rt△ABC中 ( http: / / www.21cnjy.com ),AB=4,BC=3 ,点D在斜边AB 上,连接CD把△ACD沿直线CD 翻折,使点A落在同一平面内的点A'处.当A'D与Rt△ABC的直角边垂直时, AD的长为 .
( http: / / www.21cnjy.com / )
18.如图,在平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,反比例函数的图象经过顶点C和对角线OB的中点D.作交y轴于点E.若的面积为12,则k的值为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
三、解答题
19.如图, ,点P在 上移动,当以P,C,D为顶点的三角形与 相似时,求 的长. 【出处:21教育名师】
( http: / / www.21cnjy.com / )
20.已知:如图,在 中, .求证: .
( http: / / www.21cnjy.com / )
21.如图,Rt△ABC中,∠A ( http: / / www.21cnjy.com )CB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?21世纪教育网版权所有
( http: / / www.21cnjy.com / )
22.如图,点D在 的内部, , , , ,求AD的长.
( http: / / www.21cnjy.com / )
23.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长21·cn·jy·com
( http: / / www.21cnjy.com / )
24.如图,小明同学为了测量教学楼的高度 ,先在操场上点A处放一面镜子,从点A处后退 到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动 放在C处,从点C处向后退 点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度 , 为 ,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度 .
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】D
11.【答案】2.5
12.【答案】2
13.【答案】80
14.【答案】
15.【答案】8
16.【答案】300
17.【答案】1或
18.【答案】32
19.【答案】解:设DP=x,则BP=BD-x=14-x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当 时,△ABP∽△CDP,即 ,
解得 ;
当 时,△ABP∽△PDC,即 ,
整理得x2-14x+24=0,
解得x1=2,x2=12,
BP=14-2=12,BP=14-12=2,
∴当BP为8.4或2或12时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
20.【答案】证明:∵ ,
∴ .
∵ , 且 ,
∴ ,
∴ .
21.【答案】解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm,
分两种情况:
①当∠EDB=∠ACB=90°时,
DE∥AC,△EBD∽△ABC,
∵D为BC的中点,
∴BD=CD= BC=1cm,E为AB的中点,AE=BE= AB=2cm,
∴t=2s;
②当∠DEB=∠ACB=90°时,
∵∠B=∠B,
∴△DBE∽△ABC,
∴∠BDE=∠A=30°,
∴BE= BD=cm,
∴AE=3.5cm,
∴t=3.5s;
综上所述:当以B、D、E为顶点的三角形与△ABC相似时,t的值为2或3.5;
22.【答案】解:延长AD,如图所示
. ( http: / / www.21cnjy.com / )
∵∠1+∠BAC=180°,∠1+∠BDE=180°,
∴∠BAC=∠BDE.
又∵∠BAC=∠BAD+∠CAD,∠BDE=∠BAD+∠B,
∴∠B=∠CAD.
∵∠1=∠2,
∴△ABD∽△CAD,
∴ ,即 ,
∴ .
23.【答案】解::∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴
∴ ,
∴AD=4.
24.【答案】解:由已知得, , , ,
, ,
( http: / / www.21cnjy.com / )
∴在 和 中
∴
∴ ,即 ,
∴ ,
在 和 中
∴
∴ ,即 ,
∴
∴ ,
∴
∴ ,
答:教学楼的高度 为 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
