28.1 锐角三角函数同步练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册28.1锐角三角函数小测
一、单选题
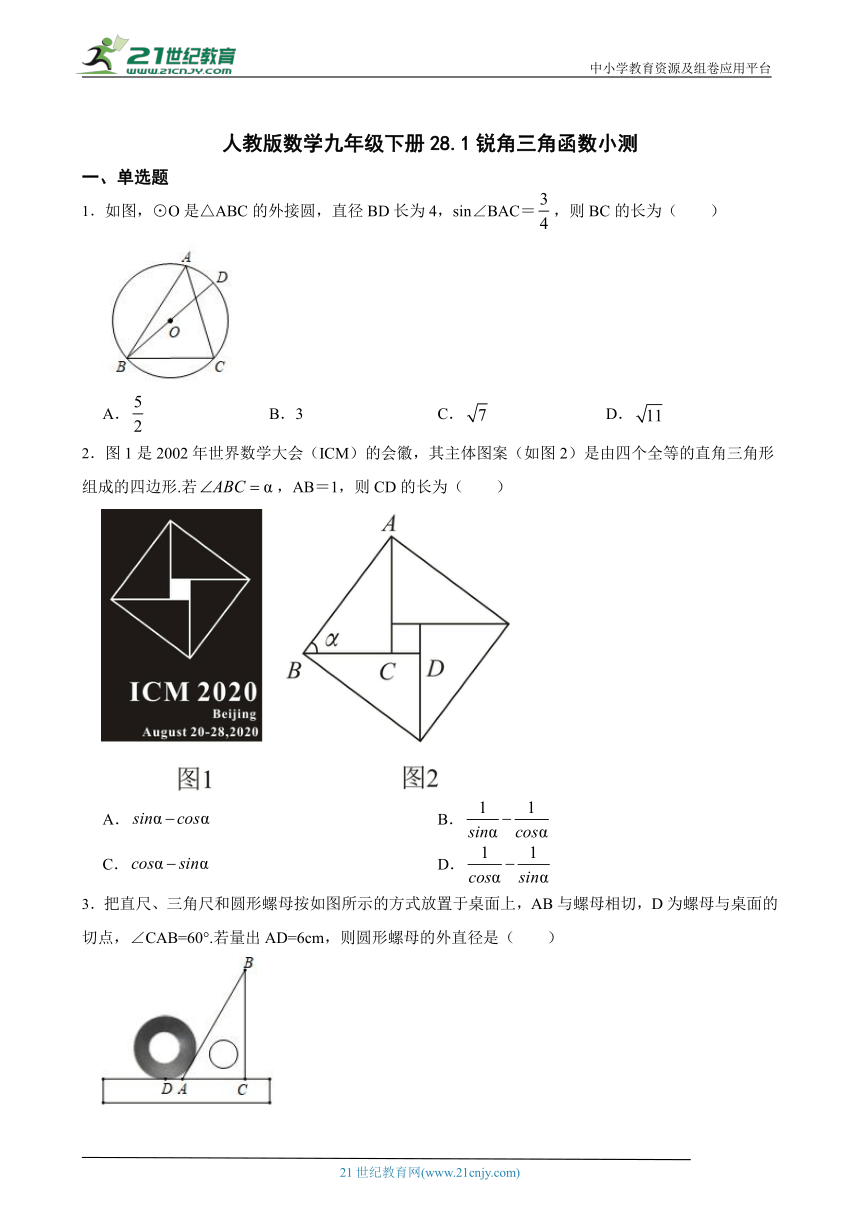
1.如图,⊙O是△ABC的外接圆,直径BD长为4,sin∠BAC=,则BC的长为( )
( http: / / www.21cnjy.com / )
A. B.3 C. D.
2.图1是2002年世界数学大会(ICM)的会徽,其主体图案(如图2)是由四个全等的直角三角形组成的四边形.若,AB=1,则CD的长为( )21教育网
( http: / / www.21cnjy.com / )
A. B.
C. D.
3.把直尺、三角尺和圆形螺母按如图所示的方 ( http: / / www.21cnjy.com )式放置于桌面上,AB与螺母相切,D为螺母与桌面的切点,∠CAB=60°.若量出AD=6cm,则圆形螺母的外直径是( )21cnjy.com
( http: / / www.21cnjy.com / )
A.cm B.12cm C.cm D.cm
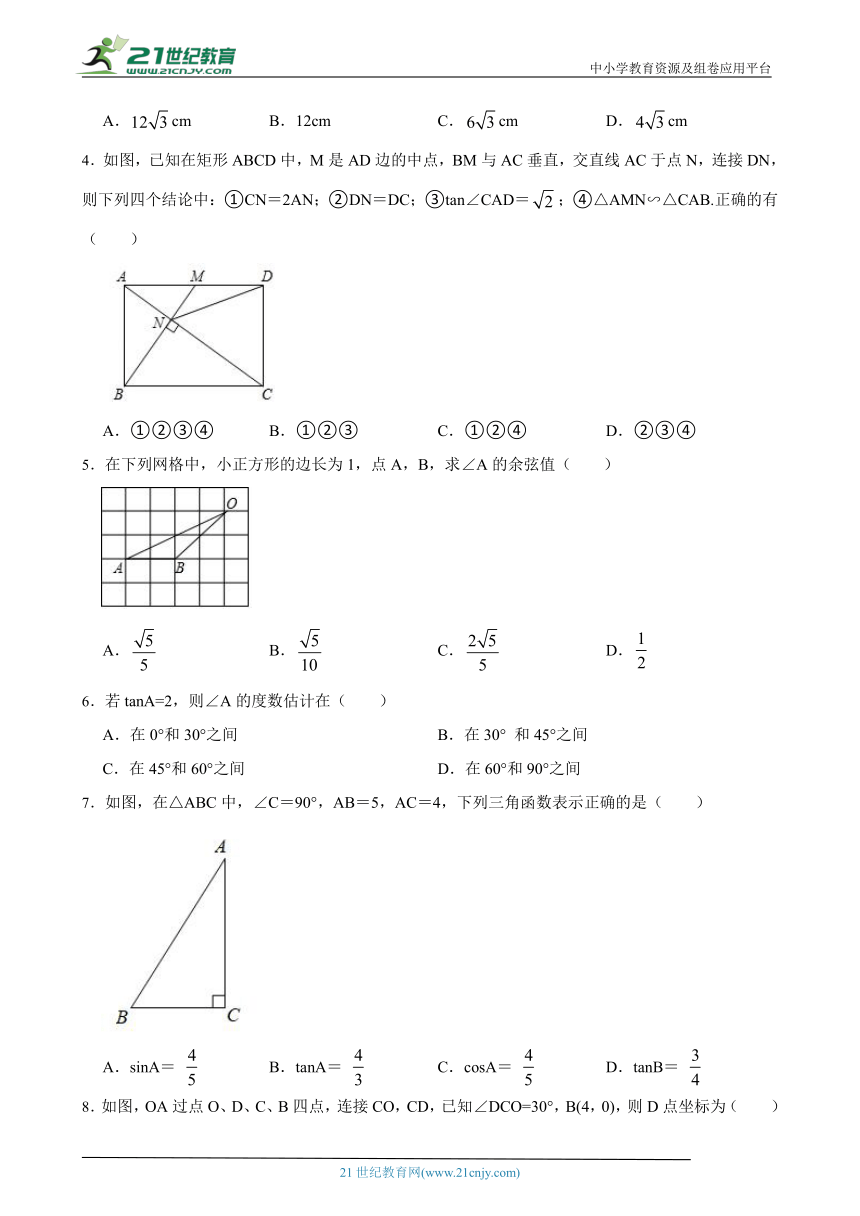
4.如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.①②③④ B.①②③ C.①②④ D.②③④
5.在下列网格中,小正方形的边长为1,点A,B,求∠A的余弦值( )
( http: / / www.21cnjy.com / )
A. B. C. D.
6.若tanA=2,则∠A的度数估计在( )
A.在0°和30°之间 B.在30° 和45°之间
C.在45°和60°之间 D.在60°和90°之间
7.如图,在△ABC中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是( )
( http: / / www.21cnjy.com / )
A.sinA= B.tanA= C.cosA= D.tanB=
8.如图,OA过点O、D、C、B四点,连接CO,CD,已知∠DCO=30°,B(4,0),则D点坐标为( )
( http: / / www.21cnjy.com / )
A.(0,2) B.(0, ) C.(0, ) D.(0,3)
9.如图,在平面直角坐标系中, 的顶点A,C的坐标分别是 , , , ,函数 的图象经过点B,则k的值为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在 ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作 ,交边AB于点E,G是 的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( ) 21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
11.将直线向下平移1个单位长度得到直线l,直线l与x轴交于点A,与y轴交于点B,则 .www.21-cn-jy.com
12.如图,墙上有一个矩形门洞ABCD,现要将其改为直径为4m的圆弧形,圆弧经过点B,C分别交AB,CD于E,F.若m,m,则要打掉的墙体面积为 .
( http: / / www.21cnjy.com / )
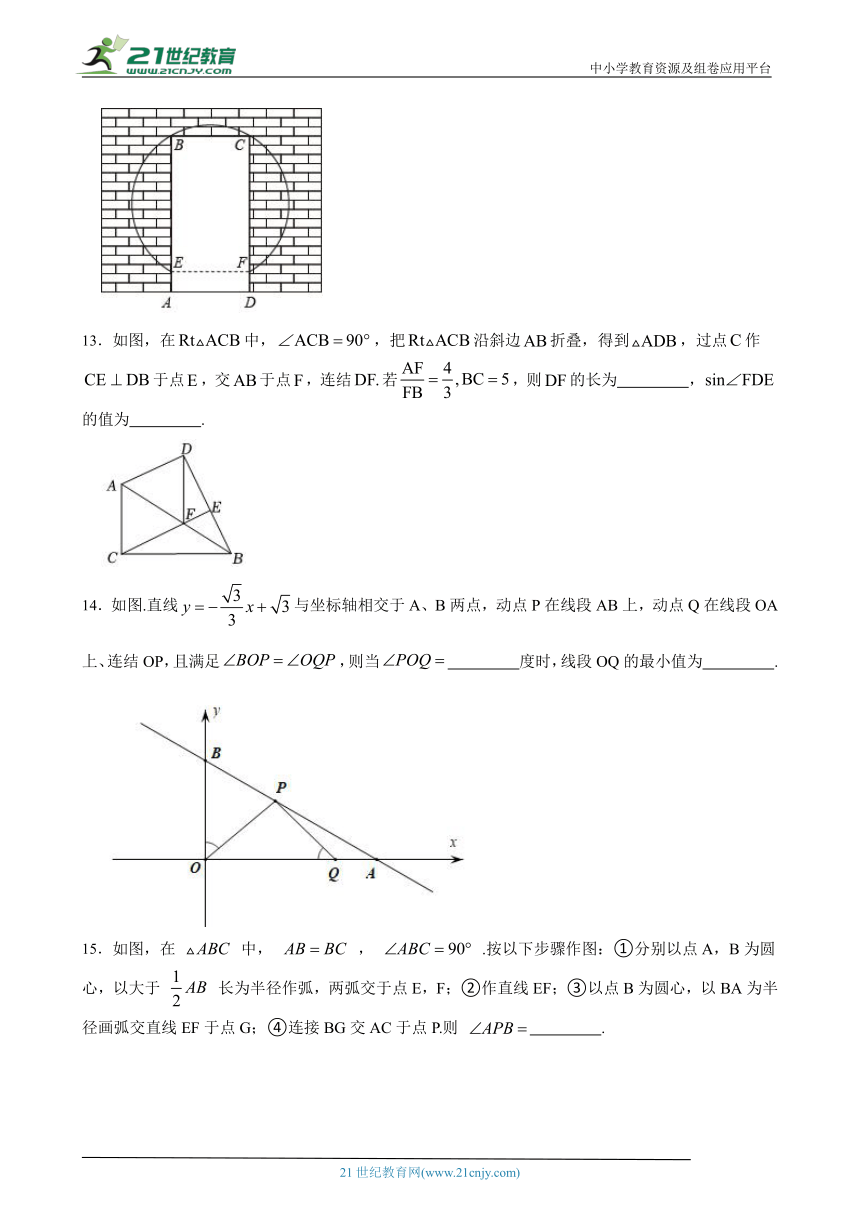
13.如图,在中,,把沿斜边折叠,得到,过点作于点,交于点,连结若,则的长为 ,的值为 .2·1·c·n·j·y
( http: / / www.21cnjy.com / )
14.如图.直线与坐标轴相交于A、B两点,动点P在线段AB上,动点Q在线段OA上、连结OP,且满足,则当 度时,线段OQ的最小值为 .
( http: / / www.21cnjy.com / )
15.如图,在 中, , .按以下步骤作图:①分别以点A,B为圆心,以大于 长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则 .21·世纪*教育网
( http: / / www.21cnjy.com / )
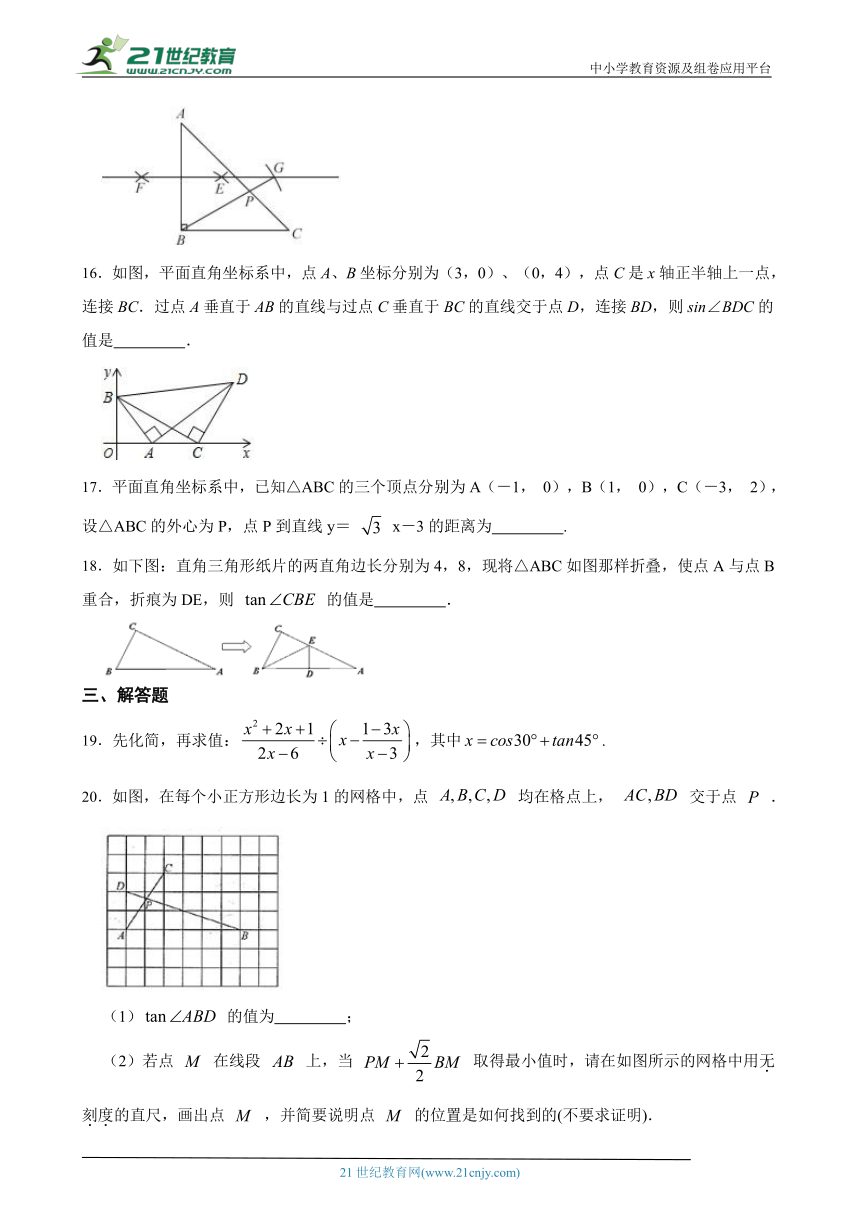
16.如图,平面直角坐标系中,点 ( http: / / www.21cnjy.com )A、B坐标分别为(3,0)、(0,4),点C是x轴正半轴上一点,连接BC.过点A垂直于AB的直线与过点C垂直于BC的直线交于点D,连接BD,则sin∠BDC的值是 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
17.平面直角坐标系中,已知△ABC的三个顶点分别为A(-1, 0),B(1, 0),C(-3, 2),设△ABC的外心为P,点P到直线y= x-3的距离为 . 21*cnjy*com
18.如下图:直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则 的值是 . 【来源:21cnj*y.co*m】
三、解答题
19.先化简,再求值:,其中.
20.如图,在每个小正方形边长为1的网格中,点 均在格点上, 交于点 .
( http: / / www.21cnjy.com / )
(1) 的值为 ;
(2)若点 在线段 上,当 取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明).
21.已知四边形ABCD是⊙O的内接四边形,∠DAB=120°,BC=CD,AD=4,AC=7,求AB的长度.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
22.已知:如图,在 中, ,垂足为 ,若 .求 的长.
( http: / / www.21cnjy.com / )
23.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
求此菱形的周长.
( http: / / www.21cnjy.com / )
24.如图,⊙O是△ABC的外接圆,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.【出处:21教育名师】
( http: / / www.21cnjy.com / )
(1)求证:AF是⊙O的切线;
(2)若AB=8,tanB= ,求线段CF、PC的长.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】()
13.【答案】;
14.【答案】30;2
15.【答案】75°
16.【答案】
17.【答案】3
18.【答案】
19.【答案】解:
=
=
=
=
=
=
当= 时,
原式=
=
=
20.【答案】(1)
(2)解:如图:取格点 ,连接 与 相交,得点 .连接 ,与 相交,得点 ,点 即为所求. 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
21.【答案】解:作DE⊥AC,BF⊥AC,
( http: / / www.21cnjy.com / )
∵BC=CD,
∴ ,
∴∠CAB=∠DAC,
∵∠DAB=120°,
∴∠DAC=∠CAB=60°,
∵DE⊥AC,
∴∠DEA=∠DEC=90°,
∴sin60°= ,cos60°= ,
∴DE=2 ,AE=2,
∵AC=7,
∴CE=5,
∴DC= ,
∴BC= ,
∵BF⊥AC,
∴∠BFA=∠BFC=90°,
∴tan60°= ,BF2+CF2=BC2,
∴BF= AF,
∴ ,
∴AF=2或AF= ,
∵cos60°= ,
∴AB=2AF,
当AF=2时,AB=2AF=4,
∴AB=AD,
∵DC=BC,AC=AC,
∴△ADC≌△ABC(SSS),
∴∠ADC=∠ABC,
∵ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=∠ABC=90°,
但AC2=49, ,
AC2≠AD2+DC2,
∴AB=4(不合题意,舍去),
当AF= 时,AB=2AF=3,
∴AB=3.
22.【答案】解:在 中, , ,
∴ ,
∴ ,
在 中, , , ,
∴
∴
23.【答案】解:∵ ,
设DE=12x,则AD=13x,勾股定理得AE=5x,
∵四边形ABCD是菱形,
∴AD=AB=13x,
∵BE=16cm,
∴13x-5x=16,解得x=2,
∴ AD=13×2=26cm ,
则菱形的周长=AD×4=26×4=104 cm
24.【答案】(1)证明:连接OC,如图所示:
( http: / / www.21cnjy.com / )
∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)∵ ,
∴ ,
设AC=3x,则BC=4x,
在Rt△ABC中,由勾股定理,得AB2=BC2+AC2,
即82=(4x)2+(3x)2,
解得 ,
∴ , .
∵OF∥BC,
∴ ,
∴ ,
∵AO=4,
∴AF=3,
∴CF=AF=3.
在Rt△AOF中,AF=3,AO=4,
∴FO=5.
∵OF∥BC,
∴△PCB∽△PFO,
∴ ,即 ,
解得 ,
∴ .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册28.1锐角三角函数小测
一、单选题
1.如图,⊙O是△ABC的外接圆,直径BD长为4,sin∠BAC=,则BC的长为( )
( http: / / www.21cnjy.com / )
A. B.3 C. D.
2.图1是2002年世界数学大会(ICM)的会徽,其主体图案(如图2)是由四个全等的直角三角形组成的四边形.若,AB=1,则CD的长为( )21教育网
( http: / / www.21cnjy.com / )
A. B.
C. D.
3.把直尺、三角尺和圆形螺母按如图所示的方 ( http: / / www.21cnjy.com )式放置于桌面上,AB与螺母相切,D为螺母与桌面的切点,∠CAB=60°.若量出AD=6cm,则圆形螺母的外直径是( )21cnjy.com
( http: / / www.21cnjy.com / )
A.cm B.12cm C.cm D.cm
4.如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.①②③④ B.①②③ C.①②④ D.②③④
5.在下列网格中,小正方形的边长为1,点A,B,求∠A的余弦值( )
( http: / / www.21cnjy.com / )
A. B. C. D.
6.若tanA=2,则∠A的度数估计在( )
A.在0°和30°之间 B.在30° 和45°之间
C.在45°和60°之间 D.在60°和90°之间
7.如图,在△ABC中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是( )
( http: / / www.21cnjy.com / )
A.sinA= B.tanA= C.cosA= D.tanB=
8.如图,OA过点O、D、C、B四点,连接CO,CD,已知∠DCO=30°,B(4,0),则D点坐标为( )
( http: / / www.21cnjy.com / )
A.(0,2) B.(0, ) C.(0, ) D.(0,3)
9.如图,在平面直角坐标系中, 的顶点A,C的坐标分别是 , , , ,函数 的图象经过点B,则k的值为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,在 ABCD中,∠A=60°,AD=2.以点A为圆心,AD为半径作 ,交边AB于点E,G是 的中点,作GF∥BC交CD于点F,以点F为旋转中心,将线段FG按逆时针方向旋转90°至线段FG′,若点G′恰好落在边BC上,则AB的长为( ) 21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
11.将直线向下平移1个单位长度得到直线l,直线l与x轴交于点A,与y轴交于点B,则 .www.21-cn-jy.com
12.如图,墙上有一个矩形门洞ABCD,现要将其改为直径为4m的圆弧形,圆弧经过点B,C分别交AB,CD于E,F.若m,m,则要打掉的墙体面积为 .
( http: / / www.21cnjy.com / )
13.如图,在中,,把沿斜边折叠,得到,过点作于点,交于点,连结若,则的长为 ,的值为 .2·1·c·n·j·y
( http: / / www.21cnjy.com / )
14.如图.直线与坐标轴相交于A、B两点,动点P在线段AB上,动点Q在线段OA上、连结OP,且满足,则当 度时,线段OQ的最小值为 .
( http: / / www.21cnjy.com / )
15.如图,在 中, , .按以下步骤作图:①分别以点A,B为圆心,以大于 长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则 .21·世纪*教育网
( http: / / www.21cnjy.com / )
16.如图,平面直角坐标系中,点 ( http: / / www.21cnjy.com )A、B坐标分别为(3,0)、(0,4),点C是x轴正半轴上一点,连接BC.过点A垂直于AB的直线与过点C垂直于BC的直线交于点D,连接BD,则sin∠BDC的值是 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
17.平面直角坐标系中,已知△ABC的三个顶点分别为A(-1, 0),B(1, 0),C(-3, 2),设△ABC的外心为P,点P到直线y= x-3的距离为 . 21*cnjy*com
18.如下图:直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则 的值是 . 【来源:21cnj*y.co*m】
三、解答题
19.先化简,再求值:,其中.
20.如图,在每个小正方形边长为1的网格中,点 均在格点上, 交于点 .
( http: / / www.21cnjy.com / )
(1) 的值为 ;
(2)若点 在线段 上,当 取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明).
21.已知四边形ABCD是⊙O的内接四边形,∠DAB=120°,BC=CD,AD=4,AC=7,求AB的长度.www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
22.已知:如图,在 中, ,垂足为 ,若 .求 的长.
( http: / / www.21cnjy.com / )
23.已知:如图,在菱形ABCD中,DE⊥AB于E,BE=16cm,
求此菱形的周长.
( http: / / www.21cnjy.com / )
24.如图,⊙O是△ABC的外接圆,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.【出处:21教育名师】
( http: / / www.21cnjy.com / )
(1)求证:AF是⊙O的切线;
(2)若AB=8,tanB= ,求线段CF、PC的长.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】D
11.【答案】
12.【答案】()
13.【答案】;
14.【答案】30;2
15.【答案】75°
16.【答案】
17.【答案】3
18.【答案】
19.【答案】解:
=
=
=
=
=
=
当= 时,
原式=
=
=
20.【答案】(1)
(2)解:如图:取格点 ,连接 与 相交,得点 .连接 ,与 相交,得点 ,点 即为所求. 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
21.【答案】解:作DE⊥AC,BF⊥AC,
( http: / / www.21cnjy.com / )
∵BC=CD,
∴ ,
∴∠CAB=∠DAC,
∵∠DAB=120°,
∴∠DAC=∠CAB=60°,
∵DE⊥AC,
∴∠DEA=∠DEC=90°,
∴sin60°= ,cos60°= ,
∴DE=2 ,AE=2,
∵AC=7,
∴CE=5,
∴DC= ,
∴BC= ,
∵BF⊥AC,
∴∠BFA=∠BFC=90°,
∴tan60°= ,BF2+CF2=BC2,
∴BF= AF,
∴ ,
∴AF=2或AF= ,
∵cos60°= ,
∴AB=2AF,
当AF=2时,AB=2AF=4,
∴AB=AD,
∵DC=BC,AC=AC,
∴△ADC≌△ABC(SSS),
∴∠ADC=∠ABC,
∵ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=∠ABC=90°,
但AC2=49, ,
AC2≠AD2+DC2,
∴AB=4(不合题意,舍去),
当AF= 时,AB=2AF=3,
∴AB=3.
22.【答案】解:在 中, , ,
∴ ,
∴ ,
在 中, , , ,
∴
∴
23.【答案】解:∵ ,
设DE=12x,则AD=13x,勾股定理得AE=5x,
∵四边形ABCD是菱形,
∴AD=AB=13x,
∵BE=16cm,
∴13x-5x=16,解得x=2,
∴ AD=13×2=26cm ,
则菱形的周长=AD×4=26×4=104 cm
24.【答案】(1)证明:连接OC,如图所示:
( http: / / www.21cnjy.com / )
∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)∵ ,
∴ ,
设AC=3x,则BC=4x,
在Rt△ABC中,由勾股定理,得AB2=BC2+AC2,
即82=(4x)2+(3x)2,
解得 ,
∴ , .
∵OF∥BC,
∴ ,
∴ ,
∵AO=4,
∴AF=3,
∴CF=AF=3.
在Rt△AOF中,AF=3,AO=4,
∴FO=5.
∵OF∥BC,
∴△PCB∽△PFO,
∴ ,即 ,
解得 ,
∴ .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
