28.2 解直角三角形及其应用同步练习(含答案)
文档属性
| 名称 | 28.2 解直角三角形及其应用同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 18:11:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册28.2解直角三角形及其应用小测
一、单选题
1.如图,在中,,,,则的面积是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
2.如图是简化的冬奥会跳台滑雪的雪道示意图,AB为助滑道,BC为着陆坡,着陆坡倾角为,A点与B点的高度差为h,A点与C点的高度差为120m,着陆坡BC长度为( )
( http: / / www.21cnjy.com / )
A. B.
C. D.
3.如图,点A到点C的距离为100米,要 ( http: / / www.21cnjy.com )测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( )
( http: / / www.21cnjy.com / )
A.100米 B.50米 C.米 D.50米
4.等腰三角形底边与底边上的高的比是2: ,则它的顶角为( )
A.30° B.45° C.60° D.120°
5.在Rt ABC中,∠C=90°,sinA ,BC=2,则AB等于( )
A. B.4 C.4 D.6
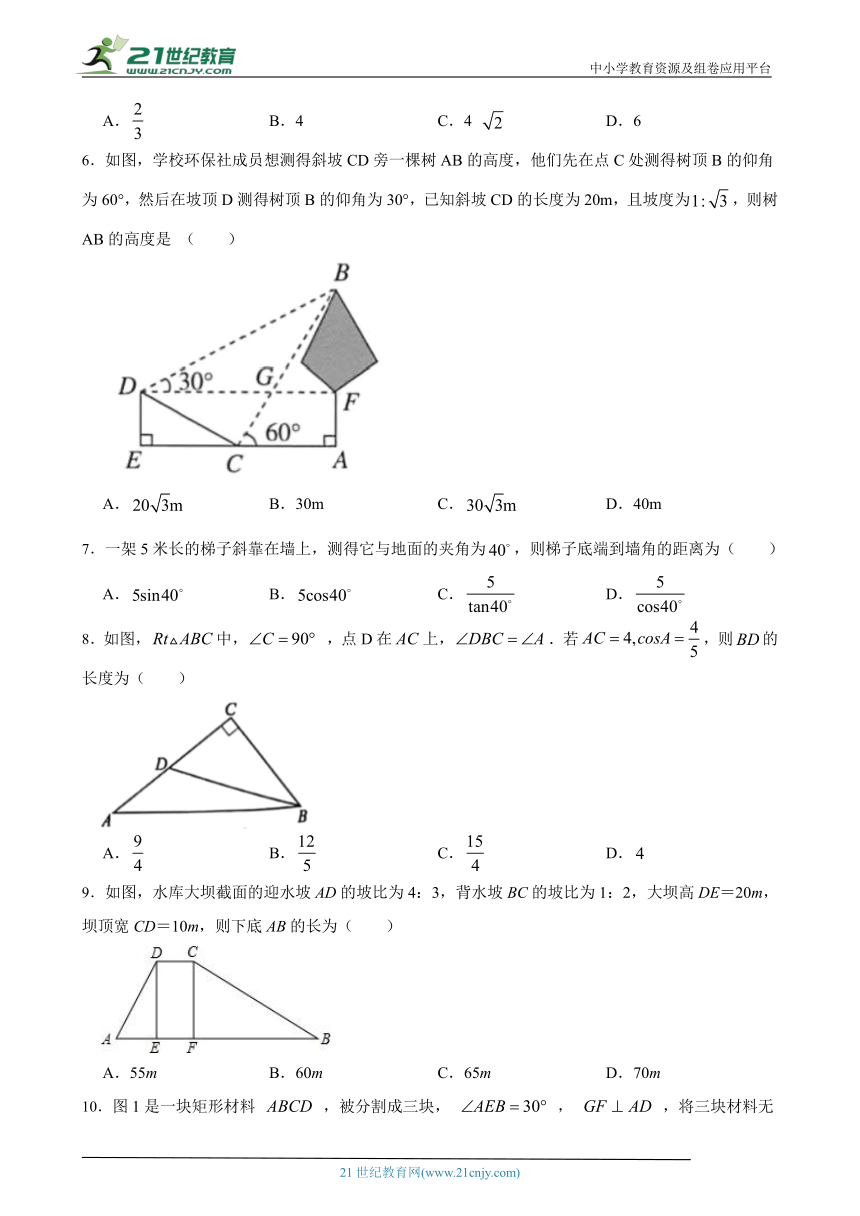
6.如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为,则树AB的高度是 ( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B.30m C. D.40m
7.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为,则梯子底端到墙角的距离为( )
A. B. C. D.
8.如图,中, ,点D在上,.若,则的长度为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9.如图,水库大坝截面的 ( http: / / www.21cnjy.com )迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( ) 21教育网
( http: / / www.21cnjy.com / )
A.55m B.60m C.65m D.70m
10.图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则 21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
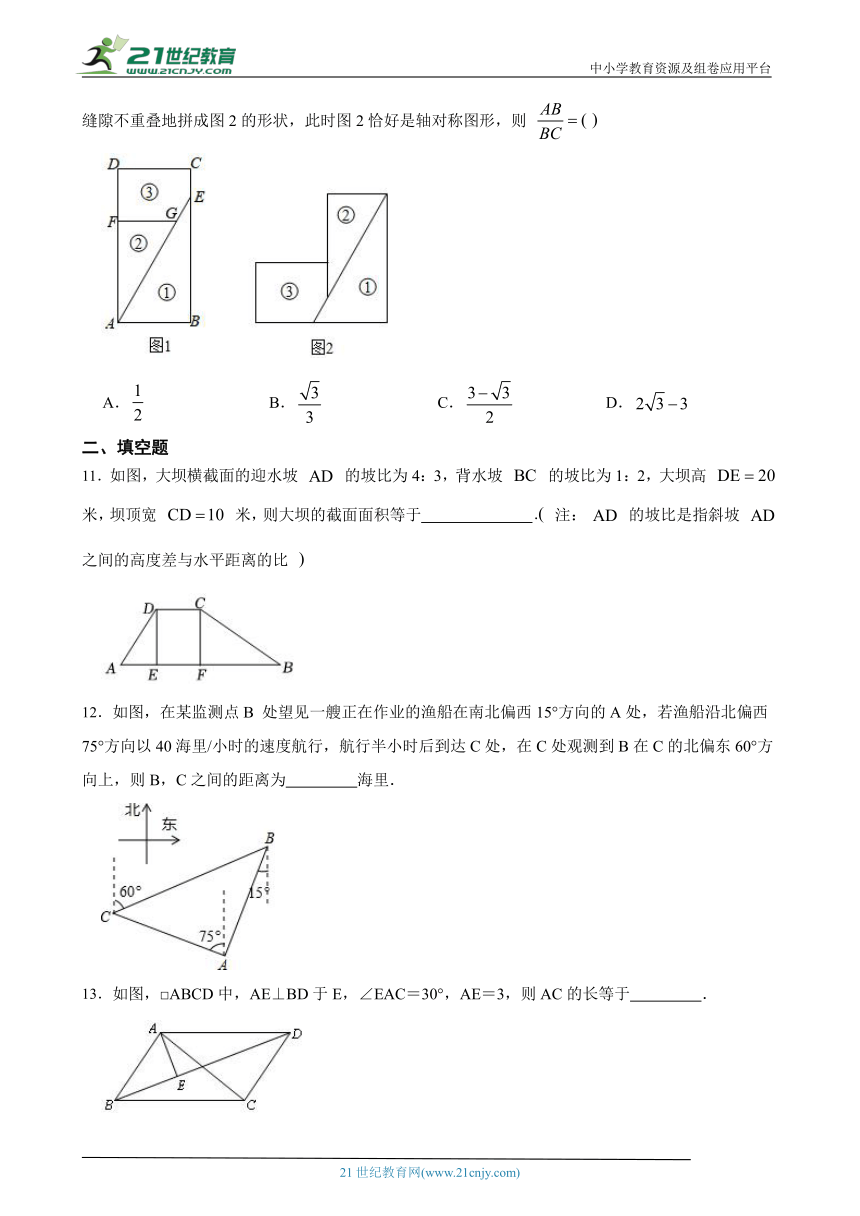
11.如图,大坝横截面的迎水坡 的坡比为4:3,背水坡 的坡比为1:2,大坝高 米,坝顶宽 米,则大坝的截面面积等于 注: 的坡比是指斜坡 之间的高度差与水平距离的比 www.21-cn-jy.com
( http: / / www.21cnjy.com / )
12.如图,在某监测点B 处望见一 ( http: / / www.21cnjy.com )艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为 海里.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
13.如图,□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 .
( http: / / www.21cnjy.com / )
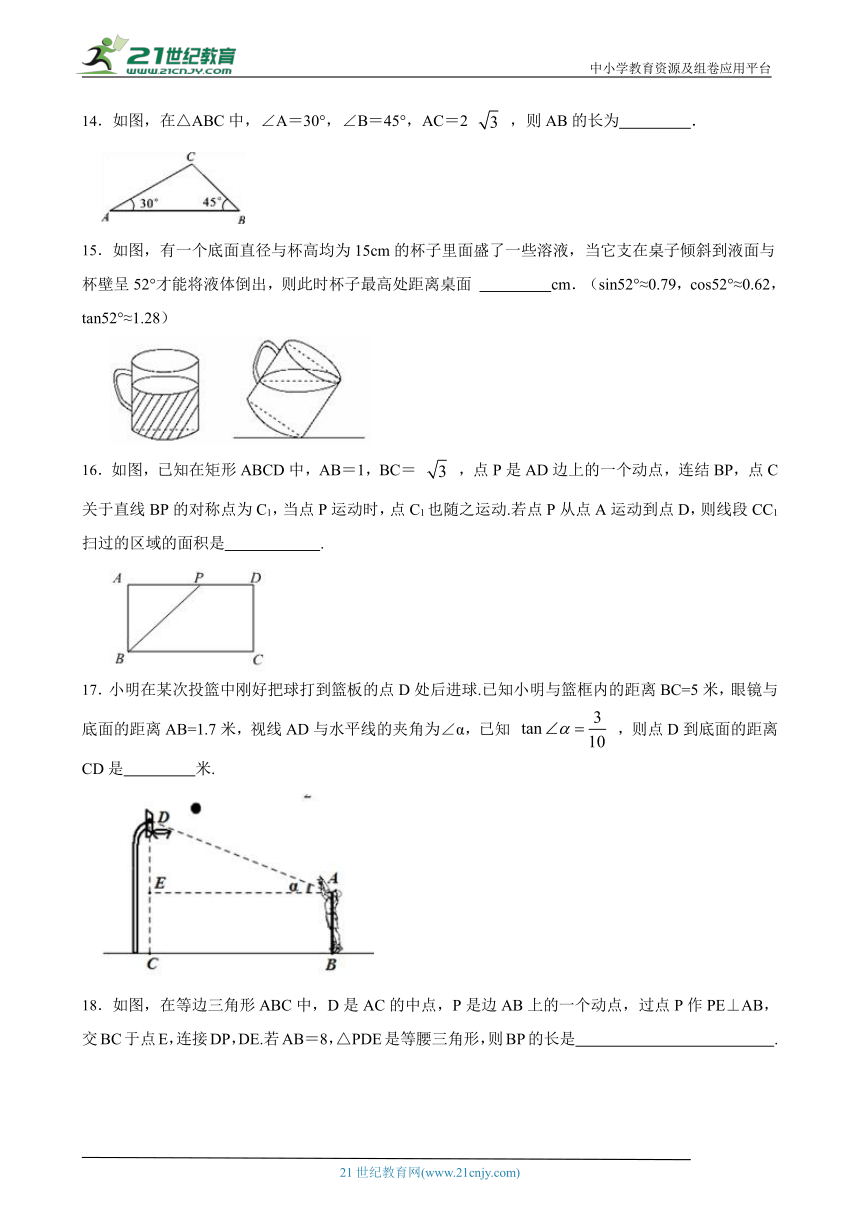
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=2 ,则AB的长为 .
15.如图,有一个底面直径 ( http: / / www.21cnjy.com )与杯高均为15cm的杯子里面盛了一些溶液,当它支在桌子倾斜到液面与杯壁呈52°才能将液体倒出,则此时杯子最高处距离桌面 cm.(sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)21·世纪*教育网
( http: / / www.21cnjy.com / )
16.如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1,当点P运动时,点C1也随之运动.若点P从点A运动到点D,则线段CC1扫过的区域的面积是 . www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
17.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框内的距离BC=5米,眼镜与底面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知 ,则点D到底面的距离CD是 米.21cnjy.com
( http: / / www.21cnjy.com / )
18.如图,在等边三角形AB ( http: / / www.21cnjy.com )C中,D是AC的中点,P是边AB上的一个动点,过点P作PE⊥AB,交BC于点E,连接DP,DE.若AB=8,△PDE是等腰三角形,则BP的长是 .
( http: / / www.21cnjy.com / )
三、解答题
19.我国海域辽阔,渔业资源丰富,如图,现有渔船以18km/h的速度在海面上沿正东方向航行,当行至A处时,发现它的东南方向有一灯塔B,船续向东航行30min后达到C处,发现灯塔B在它的南偏东15°方向,求此时渔船与灯塔B的距离.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
20.如图是一种机器零件的左视大致图形,已测得,,,,,,求点E到直线CD之间距离EF的长.(结果精确到0.1,参考数据:,,,)2-1-c-n-j-y
( http: / / www.21cnjy.com / )
21.为了维护我国海域安全,某巡逻艇从码头A出发向东航行40海里后到达B处,再从B处沿北偏东方向行驶40海里到达C处,然后沿北偏西方向航行到D处,发现码头A在正南方向.求此时巡逻艇与码头A的距离.21*cnjy*com
( http: / / www.21cnjy.com / )
22.如图(1),在豫西南邓 ( http: / / www.21cnjy.com )州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
23.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )
( http: / / www.21cnjy.com / )
24.图1是放置在水平地面上的 ( http: / / www.21cnjy.com )落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED=48°,BE=110cm,DE=80cm,求活动杆端点D离地面的高度DF.(结果精确到1cm,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】750平方米
12.【答案】20
13.【答案】4
14.【答案】3+
15.【答案】21.15
16.【答案】π+
17.【答案】3.2
18.【答案】12﹣4 或 ﹣3或4
19.【答案】解:如图,作CE⊥AB于E,
( http: / / www.21cnjy.com / )
∴AC=9km,
∵∠CAB=45°,
∴CE=AC sin45°=9km,
∵灯塔B在它的南偏东15°方向,
∴∠NCB=75°,∠CAB=45°,
∴∠B=30°,
∴BC==18(km),
答:此时渔船与灯塔B的距离为18km.
20.【答案】解:如图,分别过点A作交CD的延长线于点M,作于点N,则四边形AMFN是矩形,
( http: / / www.21cnjy.com / )
∴,,,
∴.
在中,,
∴,
∴.
在中,,
则.
在中,.
∵,
∴.
∴.
故点E到直线CD之间的距离EF的长约为37.7cm.
21.【答案】解:连接BD,如图所示,
( http: / / www.21cnjy.com / )
由题意得:AB=BC=40海里,BE∥CF,∠A=90°,∠EBC=30°,∠DCF=60°,∠ABC=∠ABE+∠EBC=120°,
∴∠BCF=180°-∠EBC=150°,
∴∠BCD=90°=∠A,
∵BD=BD,
∴△ABD≌△CBD(HL),
∴,
∴海里;
答:此时巡逻艇与码头A的距离为海里.
22.【答案】解:如图,作DM⊥AB于M,交CB于F,CG⊥DM于G,则四边形DECG为矩形,
( http: / / www.21cnjy.com / )
∴CG=DE=5,DG=EC=1.3,
设FM=x米,由题意得,∠BDM=40°,∠BFM=∠BCA=45°,
∴∠CFG=45°,BM=FM=x,
∴GF=GC=5,
∴DF=DG+GF=5+1.3=6.3,
在Rt△BDM中,tan∠BDM=,
∴DM=,
由题意得,DM﹣DF=FM,即,
解得,x≈33.2,则BA=BM+AM=38.2≈38(米),
答:该塔AB的高度约为38米.
23.【答案】解:过点C作 交AB的延长线于点C,作 于点F,如图所示:
( http: / / www.21cnjy.com / )
在 中, ,
∴ ,
在 中, ,
∴ ,
解得: ,
∴
24.【答案】解:过点E作 ,
( http: / / www.21cnjy.com / )
∵ , , ,
∴ ,
∴四边形EBFM是矩形,
∴ ,
∵∠AED=48°,
∴ ,
∴ ,
∴ .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册28.2解直角三角形及其应用小测
一、单选题
1.如图,在中,,,,则的面积是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
2.如图是简化的冬奥会跳台滑雪的雪道示意图,AB为助滑道,BC为着陆坡,着陆坡倾角为,A点与B点的高度差为h,A点与C点的高度差为120m,着陆坡BC长度为( )
( http: / / www.21cnjy.com / )
A. B.
C. D.
3.如图,点A到点C的距离为100米,要 ( http: / / www.21cnjy.com )测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( )
( http: / / www.21cnjy.com / )
A.100米 B.50米 C.米 D.50米
4.等腰三角形底边与底边上的高的比是2: ,则它的顶角为( )
A.30° B.45° C.60° D.120°
5.在Rt ABC中,∠C=90°,sinA ,BC=2,则AB等于( )
A. B.4 C.4 D.6
6.如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为,则树AB的高度是 ( )21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. B.30m C. D.40m
7.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为,则梯子底端到墙角的距离为( )
A. B. C. D.
8.如图,中, ,点D在上,.若,则的长度为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9.如图,水库大坝截面的 ( http: / / www.21cnjy.com )迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( ) 21教育网
( http: / / www.21cnjy.com / )
A.55m B.60m C.65m D.70m
10.图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则 21·cn·jy·com
( http: / / www.21cnjy.com / )
A. B. C. D.
二、填空题
11.如图,大坝横截面的迎水坡 的坡比为4:3,背水坡 的坡比为1:2,大坝高 米,坝顶宽 米,则大坝的截面面积等于 注: 的坡比是指斜坡 之间的高度差与水平距离的比 www.21-cn-jy.com
( http: / / www.21cnjy.com / )
12.如图,在某监测点B 处望见一 ( http: / / www.21cnjy.com )艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为 海里.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
13.如图,□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 .
( http: / / www.21cnjy.com / )
14.如图,在△ABC中,∠A=30°,∠B=45°,AC=2 ,则AB的长为 .
15.如图,有一个底面直径 ( http: / / www.21cnjy.com )与杯高均为15cm的杯子里面盛了一些溶液,当它支在桌子倾斜到液面与杯壁呈52°才能将液体倒出,则此时杯子最高处距离桌面 cm.(sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)21·世纪*教育网
( http: / / www.21cnjy.com / )
16.如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1,当点P运动时,点C1也随之运动.若点P从点A运动到点D,则线段CC1扫过的区域的面积是 . www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
17.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框内的距离BC=5米,眼镜与底面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知 ,则点D到底面的距离CD是 米.21cnjy.com
( http: / / www.21cnjy.com / )
18.如图,在等边三角形AB ( http: / / www.21cnjy.com )C中,D是AC的中点,P是边AB上的一个动点,过点P作PE⊥AB,交BC于点E,连接DP,DE.若AB=8,△PDE是等腰三角形,则BP的长是 .
( http: / / www.21cnjy.com / )
三、解答题
19.我国海域辽阔,渔业资源丰富,如图,现有渔船以18km/h的速度在海面上沿正东方向航行,当行至A处时,发现它的东南方向有一灯塔B,船续向东航行30min后达到C处,发现灯塔B在它的南偏东15°方向,求此时渔船与灯塔B的距离.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
20.如图是一种机器零件的左视大致图形,已测得,,,,,,求点E到直线CD之间距离EF的长.(结果精确到0.1,参考数据:,,,)2-1-c-n-j-y
( http: / / www.21cnjy.com / )
21.为了维护我国海域安全,某巡逻艇从码头A出发向东航行40海里后到达B处,再从B处沿北偏东方向行驶40海里到达C处,然后沿北偏西方向航行到D处,发现码头A在正南方向.求此时巡逻艇与码头A的距离.21*cnjy*com
( http: / / www.21cnjy.com / )
22.如图(1),在豫西南邓 ( http: / / www.21cnjy.com )州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
23.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )
( http: / / www.21cnjy.com / )
24.图1是放置在水平地面上的 ( http: / / www.21cnjy.com )落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED=48°,BE=110cm,DE=80cm,求活动杆端点D离地面的高度DF.(结果精确到1cm,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】750平方米
12.【答案】20
13.【答案】4
14.【答案】3+
15.【答案】21.15
16.【答案】π+
17.【答案】3.2
18.【答案】12﹣4 或 ﹣3或4
19.【答案】解:如图,作CE⊥AB于E,
( http: / / www.21cnjy.com / )
∴AC=9km,
∵∠CAB=45°,
∴CE=AC sin45°=9km,
∵灯塔B在它的南偏东15°方向,
∴∠NCB=75°,∠CAB=45°,
∴∠B=30°,
∴BC==18(km),
答:此时渔船与灯塔B的距离为18km.
20.【答案】解:如图,分别过点A作交CD的延长线于点M,作于点N,则四边形AMFN是矩形,
( http: / / www.21cnjy.com / )
∴,,,
∴.
在中,,
∴,
∴.
在中,,
则.
在中,.
∵,
∴.
∴.
故点E到直线CD之间的距离EF的长约为37.7cm.
21.【答案】解:连接BD,如图所示,
( http: / / www.21cnjy.com / )
由题意得:AB=BC=40海里,BE∥CF,∠A=90°,∠EBC=30°,∠DCF=60°,∠ABC=∠ABE+∠EBC=120°,
∴∠BCF=180°-∠EBC=150°,
∴∠BCD=90°=∠A,
∵BD=BD,
∴△ABD≌△CBD(HL),
∴,
∴海里;
答:此时巡逻艇与码头A的距离为海里.
22.【答案】解:如图,作DM⊥AB于M,交CB于F,CG⊥DM于G,则四边形DECG为矩形,
( http: / / www.21cnjy.com / )
∴CG=DE=5,DG=EC=1.3,
设FM=x米,由题意得,∠BDM=40°,∠BFM=∠BCA=45°,
∴∠CFG=45°,BM=FM=x,
∴GF=GC=5,
∴DF=DG+GF=5+1.3=6.3,
在Rt△BDM中,tan∠BDM=,
∴DM=,
由题意得,DM﹣DF=FM,即,
解得,x≈33.2,则BA=BM+AM=38.2≈38(米),
答:该塔AB的高度约为38米.
23.【答案】解:过点C作 交AB的延长线于点C,作 于点F,如图所示:
( http: / / www.21cnjy.com / )
在 中, ,
∴ ,
在 中, ,
∴ ,
解得: ,
∴
24.【答案】解:过点E作 ,
( http: / / www.21cnjy.com / )
∵ , , ,
∴ ,
∴四边形EBFM是矩形,
∴ ,
∵∠AED=48°,
∴ ,
∴ ,
∴ .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
