26.1.2 反比例函数的图像与性质同步练习(含答案)
文档属性
| 名称 | 26.1.2 反比例函数的图像与性质同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 18:16:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册第二十六章1.2反比例函数的图像与性质章节小测
一、单选题
1.反比例函数y=(k≠0)的图象经过点(﹣4,3),这个反比例函数的图象一定经过( )
A.(﹣4,﹣3) B.(3,﹣4)
C.(3,4) D.(﹣3,﹣4)
2.已知函数y=,经过点P1(﹣2,y1),P2(3,y2),那么( )
A.y1>0>y2 B.y2>0>y1 C.y2<y1<0 D.0<y2<y1
3.若反比例函数 在每个象限内的函数值 随 的增大而增大,则( )
A. B. C. D.
4.已知正比例函数y=k1x和反比例函数y=,在同一直角坐标系下的图象如图所示,其中符合k1 k2>0的是( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.①② B.①④ C.②③ D.③④
5.已知点A(a,y1),B(a+1,y2)在反比例函数y=(a是常数)的图象上,且y1<y2,则a的取值范围是( )2·1·c·n·j·y
A.a<0 B.a>0 C.0<a<1 D.﹣1<a<0
6.下列各点中,在函数y=图象上的是( )
A.(-2,6) B.(3,-4)
C.(-2,-6) D.(-3,4)
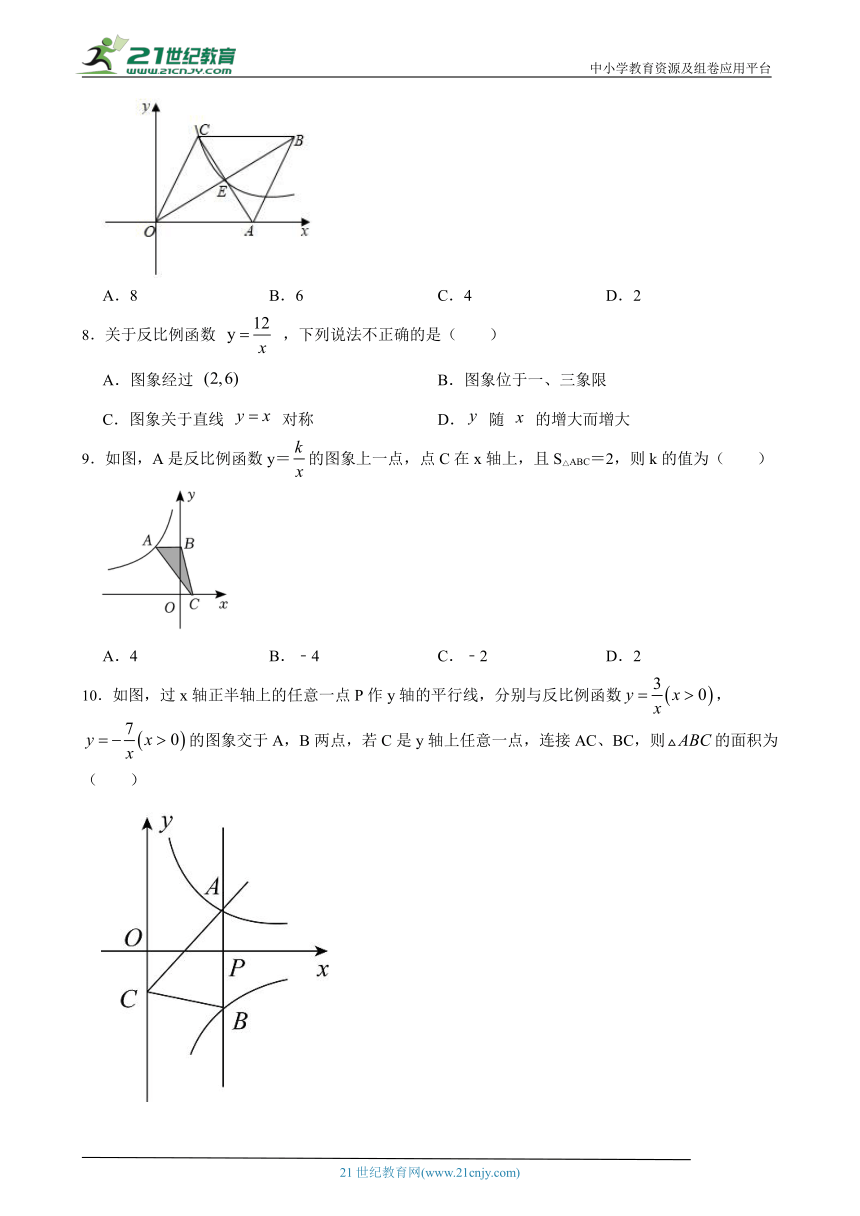
7.如图,反比例函数的图象经过的顶点和对角线的交点,顶点在轴上.若的面积为12,则的值为( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A.8 B.6 C.4 D.2
8.关于反比例函数 ,下列说法不正确的是( )
A.图象经过 B.图象位于一、三象限
C.图象关于直线 对称 D. 随 的增大而增大
9.如图,A是反比例函数y=的图象上一点,点C在x轴上,且S△ABC=2,则k的值为( )
( http: / / www.21cnjy.com / )
A.4 B.﹣4 C.﹣2 D.2
10.如图,过x轴正半轴上的任意一点P作y轴的平行线,分别与反比例函数,的图象交于A,B两点,若C是y轴上任意一点,连接AC、BC,则的面积为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.10 B. C.5 D.
二、填空题
11.已知反比例函数的图象在第二、四象限,则取值范围是
12.已知点A(﹣1,y1),B(﹣2,y2)在反比例函数y= (k>0)的图象上,则y1 y2(填“>”“<”或“=”). www-2-1-cnjy-com
13.直线y=kx与双曲线y= 交于A(x1,y1)、B(x2,y2)两点,则x1y2﹣3x2y1的值为 .
14.请写出一个反比例函数的表达式,满足条件 ( http: / / www.21cnjy.com ):在各自象限内,y的值随x值的增大而增大 .(写出一个即可)2-1-c-n-j-y
15.已知点P(1,a)在反比例函数 的图象上,其中 (m为实数),则这个函数的图象在第 象限.21*cnjy*com
16.如图,点A在双曲线y= (x>0)上,点B在双曲线y= (x>0)上,且AB∥x轴,BC∥y轴,点C在x轴上,则△ABC的面积为 . 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
17.如图,直线L:y=-x+1与坐标轴交于A、B两点,点C是反比例函数(x>0)图象上任意一点,过C分别作横纵轴的垂线CD、CG,交线段AB于E、F两点.设OE=a,EF=b,FA=c,请写出在点C移动过程中,a、b、c保持不变的数量关系 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
18.如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点C的坐标是(2,0),tan∠AOC=2,过点A的反比例函数的图象过BC边的中点D,则k的值是 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
三、综合题
19.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,顶点D在直线y=x位于第一象限的图象上,反比例函数y=(x>0)的图象经过点D,交BC于点E,AB=4.
( http: / / www.21cnjy.com / )
(1)如果BC=6,求点E的坐标;
(2)连接DE,当DE⊥OD时,求点D的坐标.
20.已知A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点.
( http: / / www.21cnjy.com / )
(1)求出m的值;
(2)写出反比例函数的表达式,并画出图象.
21.在平面直角坐标系中,设函数(k1是常数、k1>0、x>0)与函数y2=k2x(k2是常数、k2≠0)的图象交于点A,点A关于y轴的对称点为点B,若点B的坐标为(-1,2).
( http: / / www.21cnjy.com / )
(1)求k1、k2的值;
(2)当y1<y2时,直接写出x的取值范围.
22.已知反比例函数y= (k≠0)的图象经过点A(﹣3,﹣6).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,﹣5)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的增大如何变化?
23.九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:21·cn·jy·com
(1)绘制函数图象,
列表:下表是x与y的几组对应值 ( http: / / www.21cnjy.com ),其中m= .21cnjy.com
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … 1 2 4 4 2 1 m …
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;
( http: / / www.21cnjy.com / )
(2)通过观察图象,下列关于该函数的性质表述正确的是: ;(填写代号)
①函数值y随x的增大而增大;②关于y轴对称;③关于原点对称;
(3)在上图中,若直线y=2交函数的图象于A,B两点(A在B左边),连接OA.过点B作BCOA交x轴于C.则= .21世纪教育网版权所有
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】m>5
12.【答案】<
13.【答案】4
14.【答案】y=- (答案不唯一)
15.【答案】一、三
16.【答案】1.5
17.【答案】a2=b(b+c)
18.【答案】
19.【答案】(1)解: BC=6,则AD=BC=6,
当y=6时,y==6,解得:x=4,故点D(4,6),
将点D的坐标代入反比例函数表达式得:k=4×6=24,
故反比例函数表达式为:y=,
∵OB=OA+AB=8,即点E的横坐标为8,则y==3,
故点E(8,3);
(2)解:设点D(2a,3a)(a≠0),
∵四边形ABCD为矩形,故∠DAO=∠ADC=90°,
∵DE⊥OD,∠ODA=∠EDC,
又∵∠OAD=∠EDC=90°,
∴△OAD∽△ECD,
∴,即,解得:CE=,
故点E(2a+4,3a﹣),
∵点D、E都在反比例函数图象上,
∴2a 3a=(2a+4)(3a﹣),解得:a=,
故点D.
20.【答案】(1)解:∵A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点,
∴2(m+3)=m,
解得m=﹣6;
∴m的值为-6;
(2)解:由(1)知:m=﹣6,
∴B(3,-2),
设反比例函数的表达式为:,
把B(3,-2)代入得:k=﹣6,
∴反比例函数的表达式为:,
列表:
x -6 -4 -3 -2 -1 1 2 3 4 6
y 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
描点,连线,反比例函数的图象如图所示.
( http: / / www.21cnjy.com / )
21.【答案】(1)解:点B的坐标为(-1,2),点A关于y轴的对称点为点B,
点A的坐标是(1,2),
∵函数(k1是常数,k1>0,x>0),y2=k2x(k2是常数,k2≠0)的图象交于点A,
∴2=,2=k2,
∴k1=2,k2=2;
(2)解:由图象可知,当y1<y2时,x的取值范围是x>1;
22.【答案】(1)解:∵反比例函数y= (k≠0)的图象经过点A(﹣3,﹣6).
∴﹣6= ,解得,k=18
则反比例函数解析式为y= ;
(2)解:点B(4, ),C(2,﹣5),
∴4× =18,2×(﹣5)=-10,
∴点B(4, )在这个函数的图象上,
点C(2,﹣5)不在这个函数的图象上;
(3)解:∵k=18>0,
∴这个函数的图象位于一、三象限,
在每一个象限内,函数值y随自变量x的增大而减小.
23.【答案】(1)解:将x=3代入 得=, 故m= 故答案为:. 图象补充完整如图1: ( http: / / www.21cnjy.com / )21教育网
(2)②
(3)4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册第二十六章1.2反比例函数的图像与性质章节小测
一、单选题
1.反比例函数y=(k≠0)的图象经过点(﹣4,3),这个反比例函数的图象一定经过( )
A.(﹣4,﹣3) B.(3,﹣4)
C.(3,4) D.(﹣3,﹣4)
2.已知函数y=,经过点P1(﹣2,y1),P2(3,y2),那么( )
A.y1>0>y2 B.y2>0>y1 C.y2<y1<0 D.0<y2<y1
3.若反比例函数 在每个象限内的函数值 随 的增大而增大,则( )
A. B. C. D.
4.已知正比例函数y=k1x和反比例函数y=,在同一直角坐标系下的图象如图所示,其中符合k1 k2>0的是( )www.21-cn-jy.com
( http: / / www.21cnjy.com / )
A.①② B.①④ C.②③ D.③④
5.已知点A(a,y1),B(a+1,y2)在反比例函数y=(a是常数)的图象上,且y1<y2,则a的取值范围是( )2·1·c·n·j·y
A.a<0 B.a>0 C.0<a<1 D.﹣1<a<0
6.下列各点中,在函数y=图象上的是( )
A.(-2,6) B.(3,-4)
C.(-2,-6) D.(-3,4)
7.如图,反比例函数的图象经过的顶点和对角线的交点,顶点在轴上.若的面积为12,则的值为( )21·世纪*教育网
( http: / / www.21cnjy.com / )
A.8 B.6 C.4 D.2
8.关于反比例函数 ,下列说法不正确的是( )
A.图象经过 B.图象位于一、三象限
C.图象关于直线 对称 D. 随 的增大而增大
9.如图,A是反比例函数y=的图象上一点,点C在x轴上,且S△ABC=2,则k的值为( )
( http: / / www.21cnjy.com / )
A.4 B.﹣4 C.﹣2 D.2
10.如图,过x轴正半轴上的任意一点P作y轴的平行线,分别与反比例函数,的图象交于A,B两点,若C是y轴上任意一点,连接AC、BC,则的面积为( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.10 B. C.5 D.
二、填空题
11.已知反比例函数的图象在第二、四象限,则取值范围是
12.已知点A(﹣1,y1),B(﹣2,y2)在反比例函数y= (k>0)的图象上,则y1 y2(填“>”“<”或“=”). www-2-1-cnjy-com
13.直线y=kx与双曲线y= 交于A(x1,y1)、B(x2,y2)两点,则x1y2﹣3x2y1的值为 .
14.请写出一个反比例函数的表达式,满足条件 ( http: / / www.21cnjy.com ):在各自象限内,y的值随x值的增大而增大 .(写出一个即可)2-1-c-n-j-y
15.已知点P(1,a)在反比例函数 的图象上,其中 (m为实数),则这个函数的图象在第 象限.21*cnjy*com
16.如图,点A在双曲线y= (x>0)上,点B在双曲线y= (x>0)上,且AB∥x轴,BC∥y轴,点C在x轴上,则△ABC的面积为 . 【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
17.如图,直线L:y=-x+1与坐标轴交于A、B两点,点C是反比例函数(x>0)图象上任意一点,过C分别作横纵轴的垂线CD、CG,交线段AB于E、F两点.设OE=a,EF=b,FA=c,请写出在点C移动过程中,a、b、c保持不变的数量关系 .【出处:21教育名师】
( http: / / www.21cnjy.com / )
18.如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点C的坐标是(2,0),tan∠AOC=2,过点A的反比例函数的图象过BC边的中点D,则k的值是 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
三、综合题
19.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,顶点D在直线y=x位于第一象限的图象上,反比例函数y=(x>0)的图象经过点D,交BC于点E,AB=4.
( http: / / www.21cnjy.com / )
(1)如果BC=6,求点E的坐标;
(2)连接DE,当DE⊥OD时,求点D的坐标.
20.已知A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点.
( http: / / www.21cnjy.com / )
(1)求出m的值;
(2)写出反比例函数的表达式,并画出图象.
21.在平面直角坐标系中,设函数(k1是常数、k1>0、x>0)与函数y2=k2x(k2是常数、k2≠0)的图象交于点A,点A关于y轴的对称点为点B,若点B的坐标为(-1,2).
( http: / / www.21cnjy.com / )
(1)求k1、k2的值;
(2)当y1<y2时,直接写出x的取值范围.
22.已知反比例函数y= (k≠0)的图象经过点A(﹣3,﹣6).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,﹣5)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的增大如何变化?
23.九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:21·cn·jy·com
(1)绘制函数图象,
列表:下表是x与y的几组对应值 ( http: / / www.21cnjy.com ),其中m= .21cnjy.com
x … ﹣3 ﹣2 ﹣1 1 2 3 …
y … 1 2 4 4 2 1 m …
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;
( http: / / www.21cnjy.com / )
(2)通过观察图象,下列关于该函数的性质表述正确的是: ;(填写代号)
①函数值y随x的增大而增大;②关于y轴对称;③关于原点对称;
(3)在上图中,若直线y=2交函数的图象于A,B两点(A在B左边),连接OA.过点B作BCOA交x轴于C.则= .21世纪教育网版权所有
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】m>5
12.【答案】<
13.【答案】4
14.【答案】y=- (答案不唯一)
15.【答案】一、三
16.【答案】1.5
17.【答案】a2=b(b+c)
18.【答案】
19.【答案】(1)解: BC=6,则AD=BC=6,
当y=6时,y==6,解得:x=4,故点D(4,6),
将点D的坐标代入反比例函数表达式得:k=4×6=24,
故反比例函数表达式为:y=,
∵OB=OA+AB=8,即点E的横坐标为8,则y==3,
故点E(8,3);
(2)解:设点D(2a,3a)(a≠0),
∵四边形ABCD为矩形,故∠DAO=∠ADC=90°,
∵DE⊥OD,∠ODA=∠EDC,
又∵∠OAD=∠EDC=90°,
∴△OAD∽△ECD,
∴,即,解得:CE=,
故点E(2a+4,3a﹣),
∵点D、E都在反比例函数图象上,
∴2a 3a=(2a+4)(3a﹣),解得:a=,
故点D.
20.【答案】(1)解:∵A(m+3,2)和B(3,)是同一个反比例函数图象上的两个点,
∴2(m+3)=m,
解得m=﹣6;
∴m的值为-6;
(2)解:由(1)知:m=﹣6,
∴B(3,-2),
设反比例函数的表达式为:,
把B(3,-2)代入得:k=﹣6,
∴反比例函数的表达式为:,
列表:
x -6 -4 -3 -2 -1 1 2 3 4 6
y 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
描点,连线,反比例函数的图象如图所示.
( http: / / www.21cnjy.com / )
21.【答案】(1)解:点B的坐标为(-1,2),点A关于y轴的对称点为点B,
点A的坐标是(1,2),
∵函数(k1是常数,k1>0,x>0),y2=k2x(k2是常数,k2≠0)的图象交于点A,
∴2=,2=k2,
∴k1=2,k2=2;
(2)解:由图象可知,当y1<y2时,x的取值范围是x>1;
22.【答案】(1)解:∵反比例函数y= (k≠0)的图象经过点A(﹣3,﹣6).
∴﹣6= ,解得,k=18
则反比例函数解析式为y= ;
(2)解:点B(4, ),C(2,﹣5),
∴4× =18,2×(﹣5)=-10,
∴点B(4, )在这个函数的图象上,
点C(2,﹣5)不在这个函数的图象上;
(3)解:∵k=18>0,
∴这个函数的图象位于一、三象限,
在每一个象限内,函数值y随自变量x的增大而减小.
23.【答案】(1)解:将x=3代入 得=, 故m= 故答案为:. 图象补充完整如图1: ( http: / / www.21cnjy.com / )21教育网
(2)②
(3)4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
