第二十七章 相似单元检测卷(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册第二十七章相似单元复习
一、单选题
1.下列说法正确的是( )
A.对应边成比例的两个五边形相似
B.对应角相等的多边形相似
C.位似可以改变图形的形状、大小和位置
D.经过复制、放大、缩小后的四边形与原图形相似
2.一个五边形ABCDE各边的边长为2,3, ( http: / / www.21cnjy.com )4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( ) 21世纪教育网版权所有
A.8 B.6 C.4 D.2
3.如图,一张矩形纸片沿它的长边A ( http: / / www.21cnjy.com )D对折(折痕为EF),得到两个全等的小矩形,若小矩形与原来的矩形相似,那么原来矩形的长边与短边之比为( ) 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.1:1 B. :1 C. :1 D.2:1
4.已知△ABC中,∠BAC=90°,用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形,其作法错误的是( ) www-2-1-cnjy-com
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
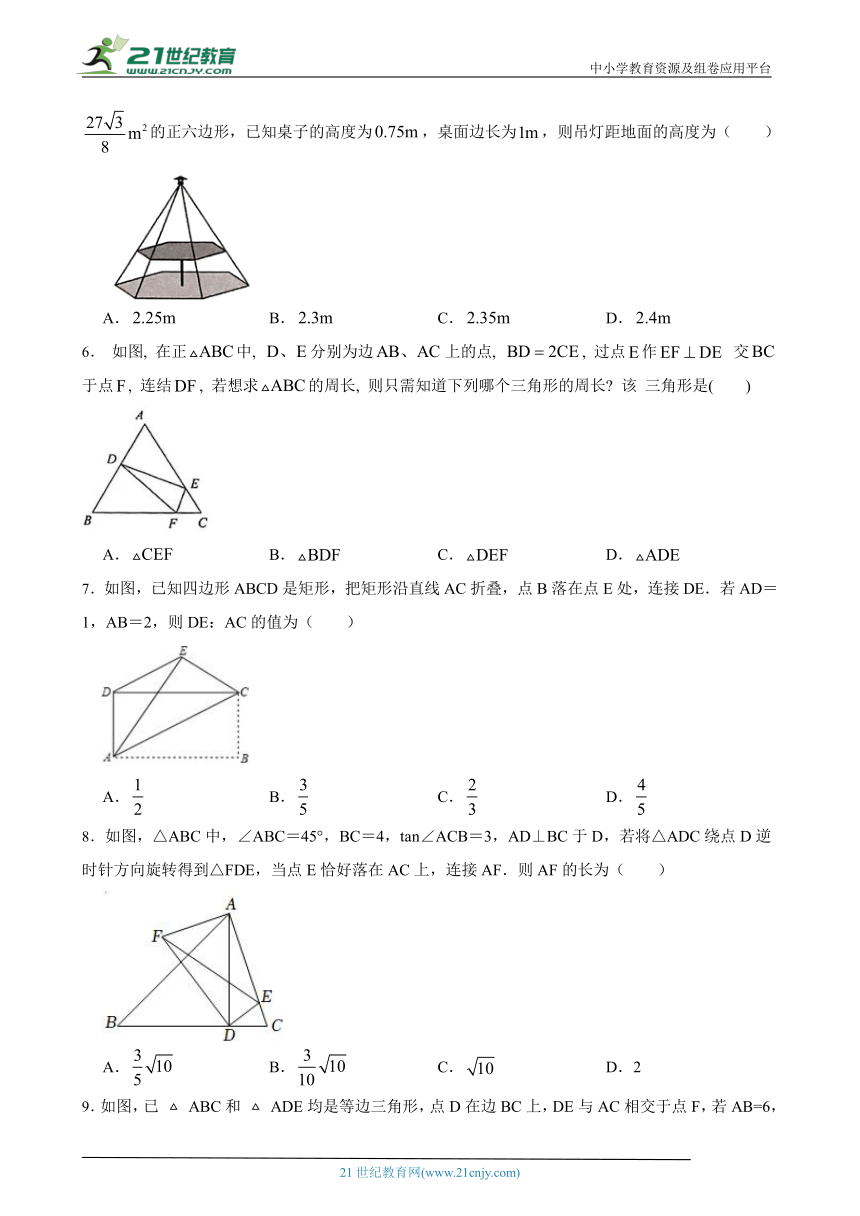
5.如图,在正六边形桌面中心正上方有一盏吊灯,在灯光下,桌面在水平地面的投影是一个面积为的正六边形,已知桌子的高度为,桌面边长为,则吊灯距地面的高度为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
6. 如图, 在正中, 分别为边上的点, , 过点作 交于点, 连结, 若想求的周长, 则只需知道下列哪个三角形的周长 该 三角形是( )
( http: / / www.21cnjy.com / )21*cnjy*com
A. B. C. D.
7.如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若AD=1,AB=2,则DE:AC的值为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,△ABC中,∠ABC=45 ( http: / / www.21cnjy.com )°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.2
9.如图,已 ABC和 ADE均是等边三角形,点D在边BC上,DE与AC相交于点F,若AB=6,AD=5,CD=4,则EF=( ) 【出处:21教育名师】
( http: / / www.21cnjy.com / )
A. B. C. D.
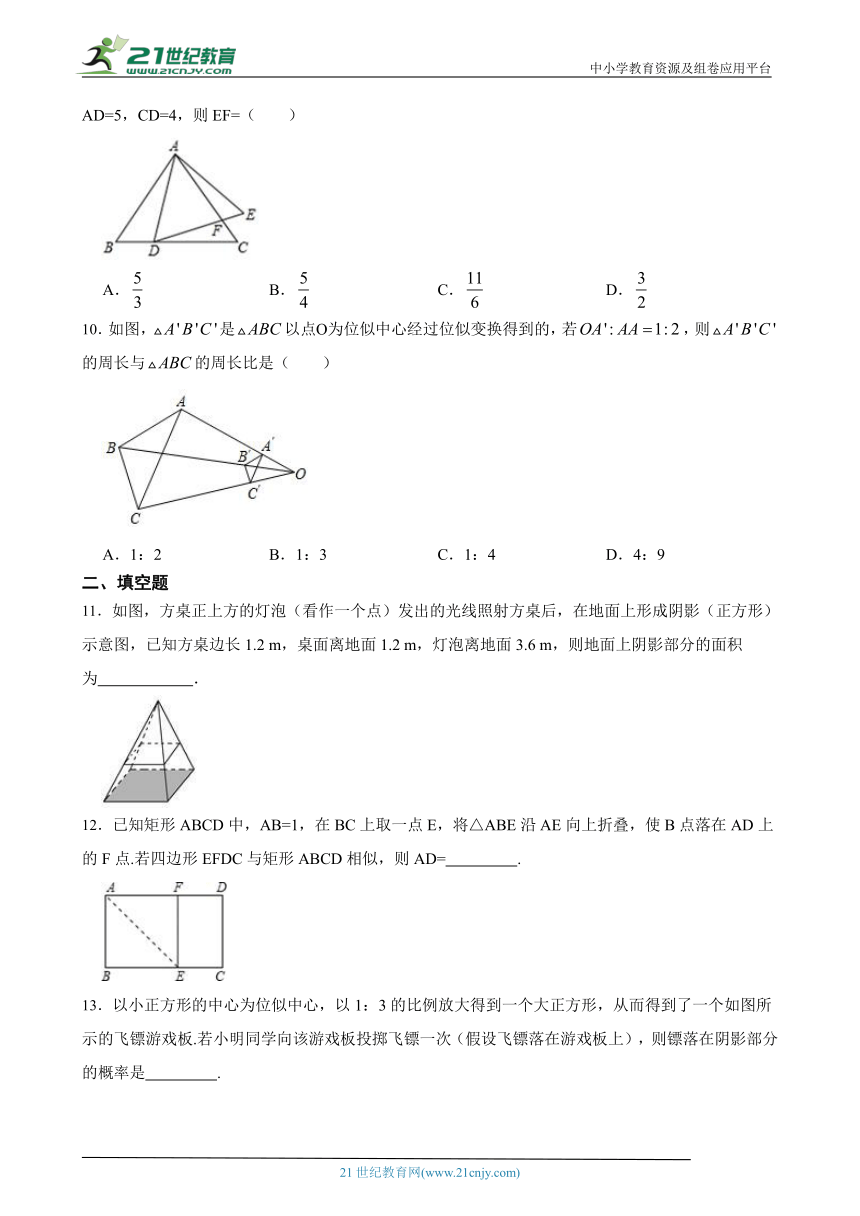
10.如图,是以点О为位似中心经过位似变换得到的,若,则的周长与的周长比是( )
( http: / / www.21cnjy.com / )
A.1:2 B.1:3 C.1:4 D.4:9
二、填空题
11.如图,方桌正上方的灯泡(看作一个点)发 ( http: / / www.21cnjy.com )出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
12.已知矩形ABCD中,AB=1 ( http: / / www.21cnjy.com ),在BC上取一点E,将△ABE沿AE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= .21教育名师原创作品
( http: / / www.21cnjy.com / )
13.以小正方形的中心为位似中心,以 ( http: / / www.21cnjy.com )1:3的比例放大得到一个大正方形,从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则镖落在阴影部分的概率是 .2·1·c·n·j·y
( http: / / www.21cnjy.com / )
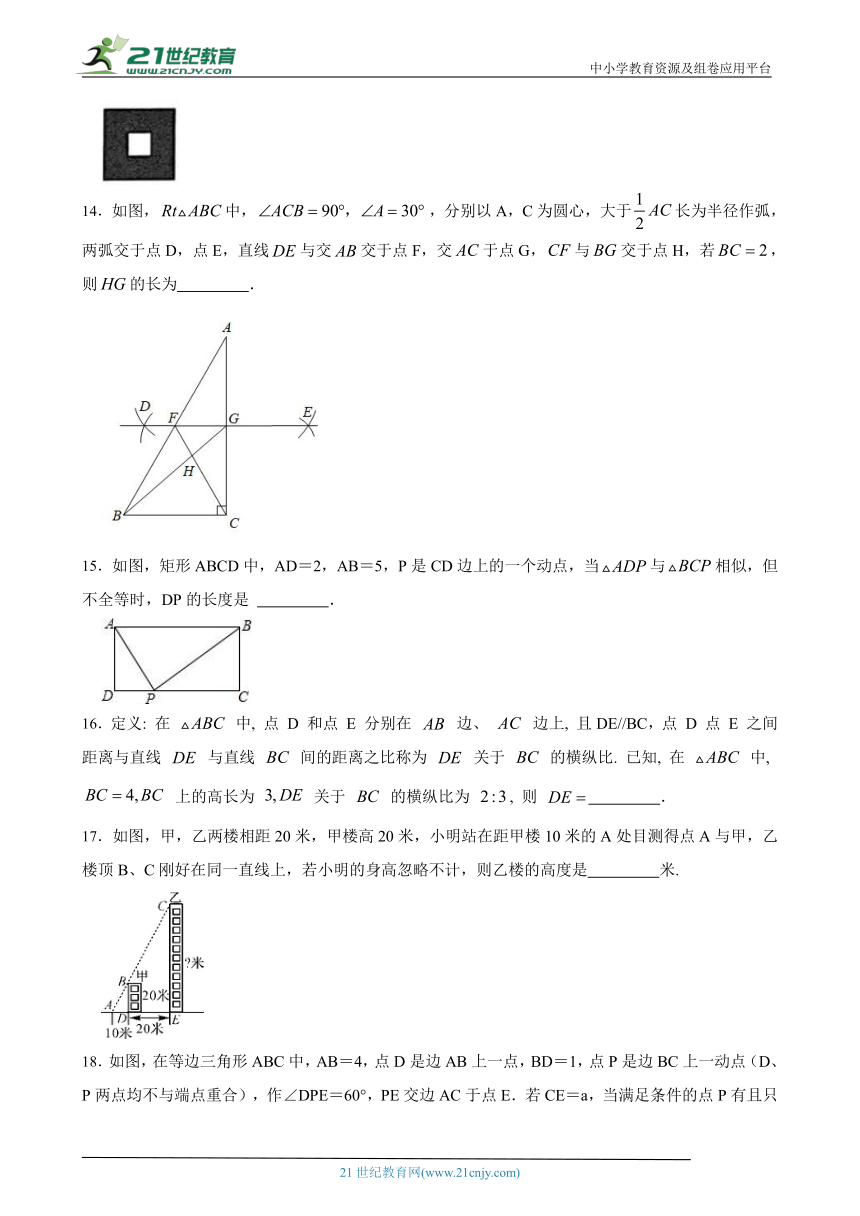
14.如图,中,,分别以A,C为圆心,大于长为半径作弧,两弧交于点D,点E,直线与交交于点F,交于点G,与交于点H,若,则的长为 .21*cnjy*com
( http: / / www.21cnjy.com / )
15.如图,矩形ABCD中,AD=2,AB=5,P是CD边上的一个动点,当与相似,但不全等时,DP的长度是 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
16.定义: 在 中, 点 D 和点 E 分别在 边、 边上, 且DE//BC,点 D 点 E 之间距离与直线 与直线 间的距离之比称为 关于 的横纵比. 已知, 在 中, 上的高长为 关于 的横纵比为 , 则 .
17.如图,甲,乙两楼相 ( http: / / www.21cnjy.com )距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲,乙楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
( http: / / www.21cnjy.com / )
18.如图,在等边三角形ABC ( http: / / www.21cnjy.com )中,AB=4,点D是边AB上一点,BD=1,点P是边BC上一动点(D、P两点均不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=a,当满足条件的点P有且只有一个时,则a的值为 .21cnjy.com
( http: / / www.21cnjy.com / )
三、解答题
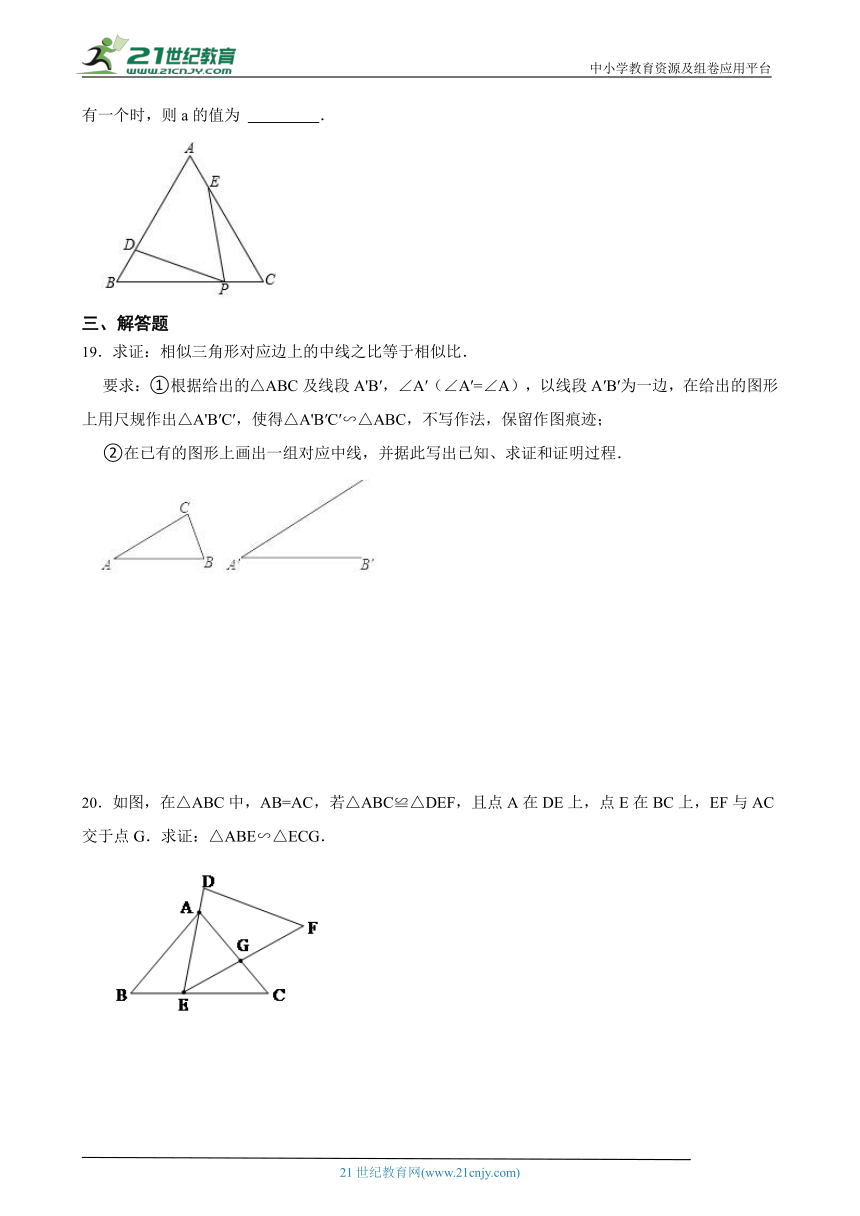
19.求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′ ( http: / / www.21cnjy.com ),∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
( http: / / www.21cnjy.com / )
20.如图,在△ABC中,AB=AC,若△ABC≌△DEF,且点A在DE上,点E在BC上,EF与AC交于点G.求证:△ABE∽△ECG.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
21.如图,在平行四边形ABCD中,AB=3,AD= ,AF交BC于E,交DC的延长线于F,且CF=1,求CE的长 21·cn·jy·com
( http: / / www.21cnjy.com / )
22.如图,一天早上,明明正向着教学楼 ( http: / / www.21cnjy.com )AB走去,他发现教学楼后面有一5G信号接收塔DC,可过了一会抬头一看:“怎么看不到接收塔了?”心里很是纳闷.经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离为30m,明明的眼睛距地面1.6m.当明明刚发现接收塔的顶部D被教学楼的顶部A挡住时,他与教学楼之间的距离为多少米?21·世纪*教育网
( http: / / www.21cnjy.com / )
23.如图,小明晚上从路灯AC走向路灯B ( http: / / www.21cnjy.com )D,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的顶部.已知小明的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
( http: / / www.21cnjy.com / )
24.在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏.如图,点 为放映机的光源, 是胶片上面的画面, 为银幕上看到的画面.若胶片上图片的规格是 ,放映的银幕规格是 ,光源 与胶片的距离是 ,则银幕应距离光源 多远时,放映的图象正好布满整个银幕?21教育网
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】3.24 m2
12.【答案】
13.【答案】
14.【答案】
15.【答案】1或4
16.【答案】
17.【答案】60
18.【答案】4
19.【答案】解:①如图所示,△A'B′C′即为所求; ( http: / / www.21cnjy.com / )②已知,如图, ( http: / / www.21cnjy.com / )△ABC∽△A'B'C', = = =k,D是AB的中点,D'是A'B'的中点,求证: =k.证明:∵D是AB的中点,D'是A'B'的中点,∴AD= AB,A'D'= A'B',∴ = ,即∵△ABC∽△A'B'C',∴ = ,∠A'=∠A,∵ = ,∠A'=∠A,∴△A'C'D'∽△ACD,∴ = =k.
20.【答案】证明:∵AB=AC,∴∠B=∠C, ∵△ABC≌△DEF,∴∠AEF=∠B
又∵∠AEF+∠CEG=∠AEC=∠B+∠BAE, ∴∠CEG=∠BAE, ∴△ABE∽△ECG .
21.【答案】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC= ,AB=3,
∴∠BAE=∠F,∠ABE=∠ECF,
∴△ABE∽△FCE,
∴ ,
∴BE=3CE,
∵BC=BE+CE= ,
∴CE= ,
22.【答案】解:如图,过点E作EG∥CD,交AB于H,
( http: / / www.21cnjy.com / )
得矩形EFCG、EFBH、HBCG和Rt△AHE、Rt△DGE,CG=BH=EF=1.6m,
则AH=AB-HB=21.6-1.6=20m,CG=DC-GC=31.6-1.6=30m,
由AH∥DG,则△AEH∽△DEG,
则EH:EG=AH:DG, EG=EH+HG=EH+30,
EH:( EH+30)=20:30,
解得EH=60m .
答:小张与教学楼的距离为60m.
23.【答案】解:∵EP⊥AB, FQ⊥AB, AC⊥AB, BD⊥AB, AC=BD=9,EP=FQ=1.5,
△APE≌△BQF,
AP=BQ, △APE∽△ABD,
设AP=BQ=x,
则 , 即 , x=5,
AB=20+2X=30
24.【答案】解:图中 是 的位似图形,
设银幕距离光源 为 时,放映的图象正好布满整个银幕,
则位似比 ,
解得 ).
答:银幕应距离光源 为 时,放映的图象正好布满整个银幕.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级下册第二十七章相似单元复习
一、单选题
1.下列说法正确的是( )
A.对应边成比例的两个五边形相似
B.对应角相等的多边形相似
C.位似可以改变图形的形状、大小和位置
D.经过复制、放大、缩小后的四边形与原图形相似
2.一个五边形ABCDE各边的边长为2,3, ( http: / / www.21cnjy.com )4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( ) 21世纪教育网版权所有
A.8 B.6 C.4 D.2
3.如图,一张矩形纸片沿它的长边A ( http: / / www.21cnjy.com )D对折(折痕为EF),得到两个全等的小矩形,若小矩形与原来的矩形相似,那么原来矩形的长边与短边之比为( ) 【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A.1:1 B. :1 C. :1 D.2:1
4.已知△ABC中,∠BAC=90°,用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形,其作法错误的是( ) www-2-1-cnjy-com
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
5.如图,在正六边形桌面中心正上方有一盏吊灯,在灯光下,桌面在水平地面的投影是一个面积为的正六边形,已知桌子的高度为,桌面边长为,则吊灯距地面的高度为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
6. 如图, 在正中, 分别为边上的点, , 过点作 交于点, 连结, 若想求的周长, 则只需知道下列哪个三角形的周长 该 三角形是( )
( http: / / www.21cnjy.com / )21*cnjy*com
A. B. C. D.
7.如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若AD=1,AB=2,则DE:AC的值为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,△ABC中,∠ABC=45 ( http: / / www.21cnjy.com )°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.2
9.如图,已 ABC和 ADE均是等边三角形,点D在边BC上,DE与AC相交于点F,若AB=6,AD=5,CD=4,则EF=( ) 【出处:21教育名师】
( http: / / www.21cnjy.com / )
A. B. C. D.
10.如图,是以点О为位似中心经过位似变换得到的,若,则的周长与的周长比是( )
( http: / / www.21cnjy.com / )
A.1:2 B.1:3 C.1:4 D.4:9
二、填空题
11.如图,方桌正上方的灯泡(看作一个点)发 ( http: / / www.21cnjy.com )出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为 .【版权所有:21教育】
( http: / / www.21cnjy.com / )
12.已知矩形ABCD中,AB=1 ( http: / / www.21cnjy.com ),在BC上取一点E,将△ABE沿AE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD= .21教育名师原创作品
( http: / / www.21cnjy.com / )
13.以小正方形的中心为位似中心,以 ( http: / / www.21cnjy.com )1:3的比例放大得到一个大正方形,从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则镖落在阴影部分的概率是 .2·1·c·n·j·y
( http: / / www.21cnjy.com / )
14.如图,中,,分别以A,C为圆心,大于长为半径作弧,两弧交于点D,点E,直线与交交于点F,交于点G,与交于点H,若,则的长为 .21*cnjy*com
( http: / / www.21cnjy.com / )
15.如图,矩形ABCD中,AD=2,AB=5,P是CD边上的一个动点,当与相似,但不全等时,DP的长度是 .2-1-c-n-j-y
( http: / / www.21cnjy.com / )
16.定义: 在 中, 点 D 和点 E 分别在 边、 边上, 且DE//BC,点 D 点 E 之间距离与直线 与直线 间的距离之比称为 关于 的横纵比. 已知, 在 中, 上的高长为 关于 的横纵比为 , 则 .
17.如图,甲,乙两楼相 ( http: / / www.21cnjy.com )距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲,乙楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
( http: / / www.21cnjy.com / )
18.如图,在等边三角形ABC ( http: / / www.21cnjy.com )中,AB=4,点D是边AB上一点,BD=1,点P是边BC上一动点(D、P两点均不与端点重合),作∠DPE=60°,PE交边AC于点E.若CE=a,当满足条件的点P有且只有一个时,则a的值为 .21cnjy.com
( http: / / www.21cnjy.com / )
三、解答题
19.求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′ ( http: / / www.21cnjy.com ),∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
( http: / / www.21cnjy.com / )
20.如图,在△ABC中,AB=AC,若△ABC≌△DEF,且点A在DE上,点E在BC上,EF与AC交于点G.求证:△ABE∽△ECG.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
21.如图,在平行四边形ABCD中,AB=3,AD= ,AF交BC于E,交DC的延长线于F,且CF=1,求CE的长 21·cn·jy·com
( http: / / www.21cnjy.com / )
22.如图,一天早上,明明正向着教学楼 ( http: / / www.21cnjy.com )AB走去,他发现教学楼后面有一5G信号接收塔DC,可过了一会抬头一看:“怎么看不到接收塔了?”心里很是纳闷.经过了解,教学楼、接收塔的高分别是21.6m和31.6m,它们之间的距离为30m,明明的眼睛距地面1.6m.当明明刚发现接收塔的顶部D被教学楼的顶部A挡住时,他与教学楼之间的距离为多少米?21·世纪*教育网
( http: / / www.21cnjy.com / )
23.如图,小明晚上从路灯AC走向路灯B ( http: / / www.21cnjy.com )D,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的顶部.已知小明的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
( http: / / www.21cnjy.com / )
24.在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏.如图,点 为放映机的光源, 是胶片上面的画面, 为银幕上看到的画面.若胶片上图片的规格是 ,放映的银幕规格是 ,光源 与胶片的距离是 ,则银幕应距离光源 多远时,放映的图象正好布满整个银幕?21教育网
( http: / / www.21cnjy.com / )
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】3.24 m2
12.【答案】
13.【答案】
14.【答案】
15.【答案】1或4
16.【答案】
17.【答案】60
18.【答案】4
19.【答案】解:①如图所示,△A'B′C′即为所求; ( http: / / www.21cnjy.com / )②已知,如图, ( http: / / www.21cnjy.com / )△ABC∽△A'B'C', = = =k,D是AB的中点,D'是A'B'的中点,求证: =k.证明:∵D是AB的中点,D'是A'B'的中点,∴AD= AB,A'D'= A'B',∴ = ,即∵△ABC∽△A'B'C',∴ = ,∠A'=∠A,∵ = ,∠A'=∠A,∴△A'C'D'∽△ACD,∴ = =k.
20.【答案】证明:∵AB=AC,∴∠B=∠C, ∵△ABC≌△DEF,∴∠AEF=∠B
又∵∠AEF+∠CEG=∠AEC=∠B+∠BAE, ∴∠CEG=∠BAE, ∴△ABE∽△ECG .
21.【答案】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC= ,AB=3,
∴∠BAE=∠F,∠ABE=∠ECF,
∴△ABE∽△FCE,
∴ ,
∴BE=3CE,
∵BC=BE+CE= ,
∴CE= ,
22.【答案】解:如图,过点E作EG∥CD,交AB于H,
( http: / / www.21cnjy.com / )
得矩形EFCG、EFBH、HBCG和Rt△AHE、Rt△DGE,CG=BH=EF=1.6m,
则AH=AB-HB=21.6-1.6=20m,CG=DC-GC=31.6-1.6=30m,
由AH∥DG,则△AEH∽△DEG,
则EH:EG=AH:DG, EG=EH+HG=EH+30,
EH:( EH+30)=20:30,
解得EH=60m .
答:小张与教学楼的距离为60m.
23.【答案】解:∵EP⊥AB, FQ⊥AB, AC⊥AB, BD⊥AB, AC=BD=9,EP=FQ=1.5,
△APE≌△BQF,
AP=BQ, △APE∽△ABD,
设AP=BQ=x,
则 , 即 , x=5,
AB=20+2X=30
24.【答案】解:图中 是 的位似图形,
设银幕距离光源 为 时,放映的图象正好布满整个银幕,
则位似比 ,
解得 ).
答:银幕应距离光源 为 时,放映的图象正好布满整个银幕.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
