人教版五年级下学期数学9总复习(课件)(共19张PPT)
文档属性
| 名称 | 人教版五年级下学期数学9总复习(课件)(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
总复习
整理复习
知识梳理
在探索图形的活动中,我们发现了多个小正方体拼成的大正方体涂色的规律。你能说一说吗?
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
因数和倍数的概念
因数 求因数、倍数的方法
和 2、5、3的倍数的特征
倍数 偶数与奇数
质数与合数的概念
100以内的质数
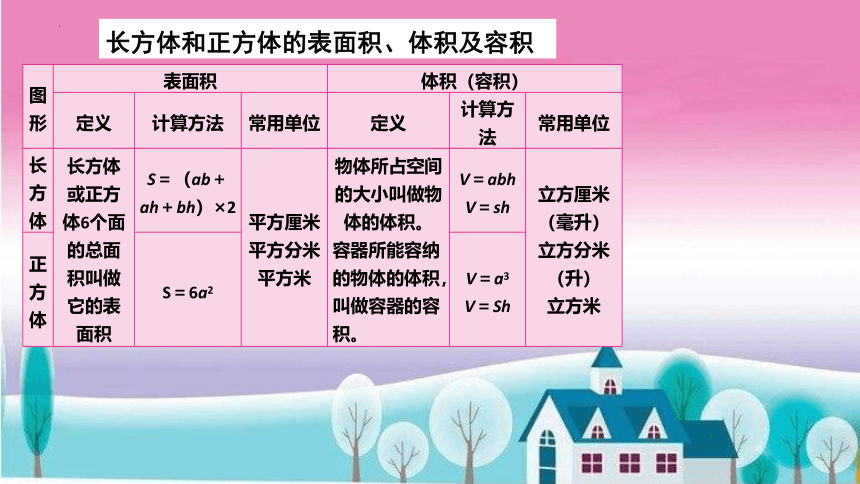
长方体和正方体的表面积、体积及容积
图形 表面积 体积(容积)
定义 计算方法 常用单位 定义 计算方法 常用单位
长方体 长方体或正方体6个面的总面积叫做它的表面积 S=(ab+ah+bh)×2 平方厘米 平方分米 平方米 物体所占空间的大小叫做物体的体积。 容器所能容纳的物体的体积,叫做容器的容积。 V=abh V=sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 S=6a2 V=a3 V=Sh
解决问题的三个步骤:
阅读与理解
分析与解答
回顾与反思
知识梳理
在找次品的活动中,你又有什么发现?最优的方法是什么?
把待测的物品数量平均分成3份,不能平均分的尽量平均分,保证有两份数量相同,并只比另一份多1或少1,这是最优的方法。
难点突破
1.(1)我们学过的统计知识中,最清楚地表示数量增减变化情况的是( )统计图。
(2)医生需要监测病人体温情况,应选用( )统计图。
(3)统计第26-30届奥运会我国运动员获得的金牌数和美国运动员获得的金牌数的变化情况,应选用( )统计图比较合适。
折线
折线
复式折线
1、2的倍数的特征:个位上是0、2、4、6、8的数都是2的倍数,例如,2、4、12、16、20、28、128等。5的倍数的特征:个位上是0或5的数都是5的倍数,例如,5、10、15、20、35、135等。3的倍数的特征:一个数各位上的数字的和是3的倍数,这个数就是3的倍数,例如,3、6、9、18、27、138等。
2、整数中,是2的倍数的数叫偶数,例如,0、2、8、16、124等,整数中,不是2的倍数的数叫奇数,例如,1、3、5、13、123等。
准确辨析,仔细判断。(对的画“√”,错的画“×”)
[★★★]
(1)一个自然数不是质数就是合数。 ( )
(2)真分数一定比1小,假分数一定比1大。 ( )
×
×
“1”既不是质数,也不是合数。
“大于1或等于1的分数叫做假分数”,例如 。
难点突破
0
销售额/万元
400
600
800
1000
1200
1400
1600
1800
2000
1
2
月份
3
4
甲、乙商场2012年1-4月销售额统计图
甲
乙
1100
1300
700
850
720
550
500
550
甲、乙两商场1-4月的销售额都呈下降趋势。
(2)包装这个盒子至少需要多少平方厘米的彩纸
(接缝处忽略不计)
(10×15+10×8+15×8)×2=700(cm2)
答:包装这个盒子至少需要700 cm2的彩纸。
随堂检测
4. 有15盒饼干,其中的14盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干?
平衡:(2次)
平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
15(5,5,5)5,5
平衡:(2次)
不平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
判断
1、自然数按照因数的个数分为 质数和合数。( )
2、自然数不是奇数就是偶数。( )
3、自然数不是合数就是质数。( )
4、自然数个数是无限的,所以质数和合数也是无限的。( )
5、10以内的质数有1、3、5、7。( )
6、偶数中除了2以外都是合数。( )
7、质数都是奇数。( )
学习提示:先独立完成,后小组交流,全班展示。
当堂检测
随堂检测
某地区1990-2010年年人均支出和年人均食品支出如下图所示。
(1)每年年人均食品支出各占年人均支出的几分之几?
(2)比较这几个分数的大小,你能发现什么?
2
1
20
9
5
2
4593
2324
5612
2831
人均食品支出占人均支出的比例先下降,后上升。
下面是2017-2021年A市第一季度人均支出和人均食品支出的情况统计表。[★★★★]
(1)请你根据表中的数据,画出复式折线统计图。
500
700
1000
2200
4200
400
500
600
1100
1600
(2)2017年A市第一季度人均食品支出占人均支出的 。
(3)2021年A市第一季度人均食品支出占人均支出的 。
4
5
8
21
下面是在一个长6 cm、宽1 cm、高3cm的长方体铁块的左、右两个角各切掉一个正方体后加工成的一个零件(如图)。 [★★★★★]
(1)给这个零件前后两面涂上黄漆,其他露出来的部分涂上蓝漆。涂黄漆和蓝漆的面积各是多少
黄漆:(6×3-1×1×2)×2=32(cm2)
蓝漆:3×1×2+6×1×2=18(cm2)
答:涂黄漆的面积是32cm2,涂蓝漆的面积是18cm2。
聪明出于勤奋,天才在于积累。
总复习
整理复习
知识梳理
在探索图形的活动中,我们发现了多个小正方体拼成的大正方体涂色的规律。你能说一说吗?
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
因数和倍数的概念
因数 求因数、倍数的方法
和 2、5、3的倍数的特征
倍数 偶数与奇数
质数与合数的概念
100以内的质数
长方体和正方体的表面积、体积及容积
图形 表面积 体积(容积)
定义 计算方法 常用单位 定义 计算方法 常用单位
长方体 长方体或正方体6个面的总面积叫做它的表面积 S=(ab+ah+bh)×2 平方厘米 平方分米 平方米 物体所占空间的大小叫做物体的体积。 容器所能容纳的物体的体积,叫做容器的容积。 V=abh V=sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 S=6a2 V=a3 V=Sh
解决问题的三个步骤:
阅读与理解
分析与解答
回顾与反思
知识梳理
在找次品的活动中,你又有什么发现?最优的方法是什么?
把待测的物品数量平均分成3份,不能平均分的尽量平均分,保证有两份数量相同,并只比另一份多1或少1,这是最优的方法。
难点突破
1.(1)我们学过的统计知识中,最清楚地表示数量增减变化情况的是( )统计图。
(2)医生需要监测病人体温情况,应选用( )统计图。
(3)统计第26-30届奥运会我国运动员获得的金牌数和美国运动员获得的金牌数的变化情况,应选用( )统计图比较合适。
折线
折线
复式折线
1、2的倍数的特征:个位上是0、2、4、6、8的数都是2的倍数,例如,2、4、12、16、20、28、128等。5的倍数的特征:个位上是0或5的数都是5的倍数,例如,5、10、15、20、35、135等。3的倍数的特征:一个数各位上的数字的和是3的倍数,这个数就是3的倍数,例如,3、6、9、18、27、138等。
2、整数中,是2的倍数的数叫偶数,例如,0、2、8、16、124等,整数中,不是2的倍数的数叫奇数,例如,1、3、5、13、123等。
准确辨析,仔细判断。(对的画“√”,错的画“×”)
[★★★]
(1)一个自然数不是质数就是合数。 ( )
(2)真分数一定比1小,假分数一定比1大。 ( )
×
×
“1”既不是质数,也不是合数。
“大于1或等于1的分数叫做假分数”,例如 。
难点突破
0
销售额/万元
400
600
800
1000
1200
1400
1600
1800
2000
1
2
月份
3
4
甲、乙商场2012年1-4月销售额统计图
甲
乙
1100
1300
700
850
720
550
500
550
甲、乙两商场1-4月的销售额都呈下降趋势。
(2)包装这个盒子至少需要多少平方厘米的彩纸
(接缝处忽略不计)
(10×15+10×8+15×8)×2=700(cm2)
答:包装这个盒子至少需要700 cm2的彩纸。
随堂检测
4. 有15盒饼干,其中的14盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干?
平衡:(2次)
平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
15(5,5,5)5,5
平衡:(2次)
不平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
判断
1、自然数按照因数的个数分为 质数和合数。( )
2、自然数不是奇数就是偶数。( )
3、自然数不是合数就是质数。( )
4、自然数个数是无限的,所以质数和合数也是无限的。( )
5、10以内的质数有1、3、5、7。( )
6、偶数中除了2以外都是合数。( )
7、质数都是奇数。( )
学习提示:先独立完成,后小组交流,全班展示。
当堂检测
随堂检测
某地区1990-2010年年人均支出和年人均食品支出如下图所示。
(1)每年年人均食品支出各占年人均支出的几分之几?
(2)比较这几个分数的大小,你能发现什么?
2
1
20
9
5
2
4593
2324
5612
2831
人均食品支出占人均支出的比例先下降,后上升。
下面是2017-2021年A市第一季度人均支出和人均食品支出的情况统计表。[★★★★]
(1)请你根据表中的数据,画出复式折线统计图。
500
700
1000
2200
4200
400
500
600
1100
1600
(2)2017年A市第一季度人均食品支出占人均支出的 。
(3)2021年A市第一季度人均食品支出占人均支出的 。
4
5
8
21
下面是在一个长6 cm、宽1 cm、高3cm的长方体铁块的左、右两个角各切掉一个正方体后加工成的一个零件(如图)。 [★★★★★]
(1)给这个零件前后两面涂上黄漆,其他露出来的部分涂上蓝漆。涂黄漆和蓝漆的面积各是多少
黄漆:(6×3-1×1×2)×2=32(cm2)
蓝漆:3×1×2+6×1×2=18(cm2)
答:涂黄漆的面积是32cm2,涂蓝漆的面积是18cm2。
聪明出于勤奋,天才在于积累。
