人教版数学九年级下册 27.2.1 相似三角形的判定 第1课时-教案
文档属性
| 名称 | 人教版数学九年级下册 27.2.1 相似三角形的判定 第1课时-教案 |  | |
| 格式 | doc | ||
| 文件大小 | 100.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 07:07:39 | ||
图片预览

文档简介
27.2.1 相似三角形的判定
第1课时
教学目标
【知识与技能】
1.了解相似三角形的概念及其表示方法;
2.掌握平行线分线段成比例定理及平行于三角形一边的直线的性质
定理;
3.掌握相似三角形判定的预备定理.
【过程与方法】
经历从探究到归纳证明的过程,发展学生的合情推理能力和逻辑思维能力.
【情感态度】
体验从一般到特殊及由特殊到一般的认知规律,发展辩证思维能力.
教学重难点
【教学重点】
平行线分线段成比例定理及判定三角形相似的预备定理.
【教学难点】
探索平行线分线段成比例定理的过程.
课前准备
无
教学过程
一、情境导入,初步认识
问题1 相似多边形的性质是否也适用于相似三角形呢?
问题2 如果△ABC与△A1B1C1相似,能类似于两个三角形全等,给出一种相似表示方法吗?△ABC与△A1B1C1的相似比为k,那么△A1B1C1与△ABC的相似比也是k吗?
问题3 如何判定两个三角形相似呢?
【教学说明】通过上述三个问题的设置,既帮助学生认识了相似三角形的一些基本知识,又为引出平行线分线段成比例定理作些铺塾,教师可釆用自问自答形式讲述这部分内容.
二、思考探究,获取新知
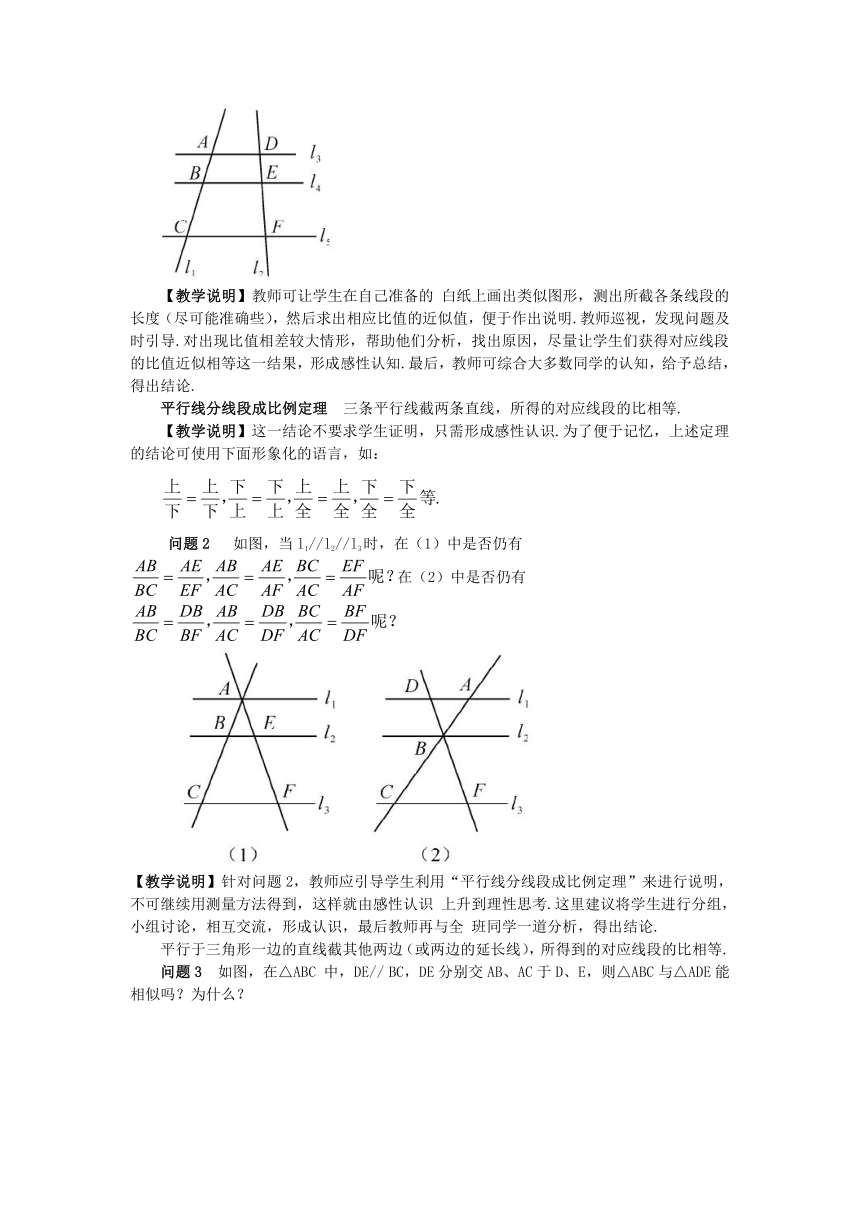
问题1 如图,任意画两条直线l1,l2,再画三条与l1,l2相交的平行线l3,l4,l5分别度量AB,BC,DE,EF长度,则相等吗?
【教学说明】教师可让学生在自己准备的 白纸上画出类似图形,测出所截各条线段的长度(尽可能准确些),然后求出相应比值的近似值,便于作出说明.教师巡视,发现问题及时引导.对出现比值相差较大情形,帮助他们分析,找出原因,尽量让学生们获得对应线段的比值近似相等这一结果,形成感性认知.最后,教师可综合大多数同学的认知,给予总结,得出结论.
平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段的比相等.
【教学说明】这一结论不要求学生证明,只需形成感性认识.为了便于记忆,上述定理的结论可使用下面形象化的语言,如:
问题2 如图,当l1//l2//l3时,在(1)中是否仍有在(2)中是否仍有
【教学说明】针对问题2,教师应引导学生利用“平行线分线段成比例定理”来进行说明,不可继续用测量方法得到,这样就由感性认识 上升到理性思考.这里建议将学生进行分组,小组讨论,相互交流,形成认识,最后教师再与全 班同学一道分析,得出结论.
平行于三角形一边的直线截其他两边(或两边的延长线),所得到的对应线段的比相等.
问题3 如图,在△ABC 中,DE// BC,DE分别交AB、AC于D、E,则△ABC与△ADE能相似吗?为什么?
问题4 如图,已知DE//BC,DE分别交AB.AC的反向延长线于D、E,则△ADE与△ABC能相似吗?为什么 ?
【教学说明】将全班学生分成两组,分别完成问题3、4的探究,教师应先给予点拨,突破难点(即添加辅助线,达到两个三角形的三边的比能相等的目的),然后学生自主完成,锻炼逻辑思维能力和推理能力.
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似 (相似三角形判定的预备定理).
三、运用新知,深化理解
1.如图,DE//BC,EF//AB,请尽可能多地找出图中的相似三角形,并
用符号表示出来.
2.如图D为△ABC中BC边的中点,E为AD 中点,连接并延长BE交
AC于F.过E作EG//AC交BC于G.
求的值;(2)求的值;(3)求的值.
3.如图,已知在△ABC中,DE//BC,AD=EC,BD=1cm,AE=4cm,BC=5cm,
求 DE 的长.
【教学说明】 让学生自主完成,也可合作完成,在练习中加深理解.教师巡视指导,及时点拨.在完成上述题目后,教师引导学生完成创 优作业中本课时的“名师导学”部分.
【答案】1.解:△ADE~△ABC,△CEF~△CAB, △ADE~△EFC.
2.解:(1)∵EG//AC,∴△DGE~△DCA,∴.
(2)∵EG//AC,E是AD的中点,∴G是CD的中点,即CG=DG.又D是BC的中点,∴BD=CD,∴BG=3CG,BC=4CG,∴ . ∵EG//FC, ∴△BEG~△BFC,∴.
(3)过D点作DH//CF,交BF于H.易得DH=AF,∴.
3.解:∵DE//BC,∴,又AD=CE,∴AD2=4,∴AD=2,∴AB=3.由DE//BC可知△ADE~△ABC,∴.
四、师生互动,课堂小结
1.这节课你学到了哪些知识?
2.你还有哪些疑惑?
【教学说明】师生以交谈方式回顾本节知识,重点应关注哪些内容,还有什么地方不太明白,及时解疑.
课后作业
完成创优作业中本课时的“课时作业”部分.
教学反思
本课时教学思路应从探究、猜想、验证归纳出发,遵循学生的理解认知能力,由浅入深、逐步推进,激发学生自主探究的学习热情,培养学生的自主学习能力.
第1课时
教学目标
【知识与技能】
1.了解相似三角形的概念及其表示方法;
2.掌握平行线分线段成比例定理及平行于三角形一边的直线的性质
定理;
3.掌握相似三角形判定的预备定理.
【过程与方法】
经历从探究到归纳证明的过程,发展学生的合情推理能力和逻辑思维能力.
【情感态度】
体验从一般到特殊及由特殊到一般的认知规律,发展辩证思维能力.
教学重难点
【教学重点】
平行线分线段成比例定理及判定三角形相似的预备定理.
【教学难点】
探索平行线分线段成比例定理的过程.
课前准备
无
教学过程
一、情境导入,初步认识
问题1 相似多边形的性质是否也适用于相似三角形呢?
问题2 如果△ABC与△A1B1C1相似,能类似于两个三角形全等,给出一种相似表示方法吗?△ABC与△A1B1C1的相似比为k,那么△A1B1C1与△ABC的相似比也是k吗?
问题3 如何判定两个三角形相似呢?
【教学说明】通过上述三个问题的设置,既帮助学生认识了相似三角形的一些基本知识,又为引出平行线分线段成比例定理作些铺塾,教师可釆用自问自答形式讲述这部分内容.
二、思考探究,获取新知
问题1 如图,任意画两条直线l1,l2,再画三条与l1,l2相交的平行线l3,l4,l5分别度量AB,BC,DE,EF长度,则相等吗?
【教学说明】教师可让学生在自己准备的 白纸上画出类似图形,测出所截各条线段的长度(尽可能准确些),然后求出相应比值的近似值,便于作出说明.教师巡视,发现问题及时引导.对出现比值相差较大情形,帮助他们分析,找出原因,尽量让学生们获得对应线段的比值近似相等这一结果,形成感性认知.最后,教师可综合大多数同学的认知,给予总结,得出结论.
平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段的比相等.
【教学说明】这一结论不要求学生证明,只需形成感性认识.为了便于记忆,上述定理的结论可使用下面形象化的语言,如:
问题2 如图,当l1//l2//l3时,在(1)中是否仍有在(2)中是否仍有
【教学说明】针对问题2,教师应引导学生利用“平行线分线段成比例定理”来进行说明,不可继续用测量方法得到,这样就由感性认识 上升到理性思考.这里建议将学生进行分组,小组讨论,相互交流,形成认识,最后教师再与全 班同学一道分析,得出结论.
平行于三角形一边的直线截其他两边(或两边的延长线),所得到的对应线段的比相等.
问题3 如图,在△ABC 中,DE// BC,DE分别交AB、AC于D、E,则△ABC与△ADE能相似吗?为什么?
问题4 如图,已知DE//BC,DE分别交AB.AC的反向延长线于D、E,则△ADE与△ABC能相似吗?为什么 ?
【教学说明】将全班学生分成两组,分别完成问题3、4的探究,教师应先给予点拨,突破难点(即添加辅助线,达到两个三角形的三边的比能相等的目的),然后学生自主完成,锻炼逻辑思维能力和推理能力.
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似 (相似三角形判定的预备定理).
三、运用新知,深化理解
1.如图,DE//BC,EF//AB,请尽可能多地找出图中的相似三角形,并
用符号表示出来.
2.如图D为△ABC中BC边的中点,E为AD 中点,连接并延长BE交
AC于F.过E作EG//AC交BC于G.
求的值;(2)求的值;(3)求的值.
3.如图,已知在△ABC中,DE//BC,AD=EC,BD=1cm,AE=4cm,BC=5cm,
求 DE 的长.
【教学说明】 让学生自主完成,也可合作完成,在练习中加深理解.教师巡视指导,及时点拨.在完成上述题目后,教师引导学生完成创 优作业中本课时的“名师导学”部分.
【答案】1.解:△ADE~△ABC,△CEF~△CAB, △ADE~△EFC.
2.解:(1)∵EG//AC,∴△DGE~△DCA,∴.
(2)∵EG//AC,E是AD的中点,∴G是CD的中点,即CG=DG.又D是BC的中点,∴BD=CD,∴BG=3CG,BC=4CG,∴ . ∵EG//FC, ∴△BEG~△BFC,∴.
(3)过D点作DH//CF,交BF于H.易得DH=AF,∴.
3.解:∵DE//BC,∴,又AD=CE,∴AD2=4,∴AD=2,∴AB=3.由DE//BC可知△ADE~△ABC,∴.
四、师生互动,课堂小结
1.这节课你学到了哪些知识?
2.你还有哪些疑惑?
【教学说明】师生以交谈方式回顾本节知识,重点应关注哪些内容,还有什么地方不太明白,及时解疑.
课后作业
完成创优作业中本课时的“课时作业”部分.
教学反思
本课时教学思路应从探究、猜想、验证归纳出发,遵循学生的理解认知能力,由浅入深、逐步推进,激发学生自主探究的学习热情,培养学生的自主学习能力.
