北师大版九年级下册 1.1.1锐角三角函数课件(共34张PPT)
文档属性
| 名称 | 北师大版九年级下册 1.1.1锐角三角函数课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 729.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 08:18:22 | ||
图片预览




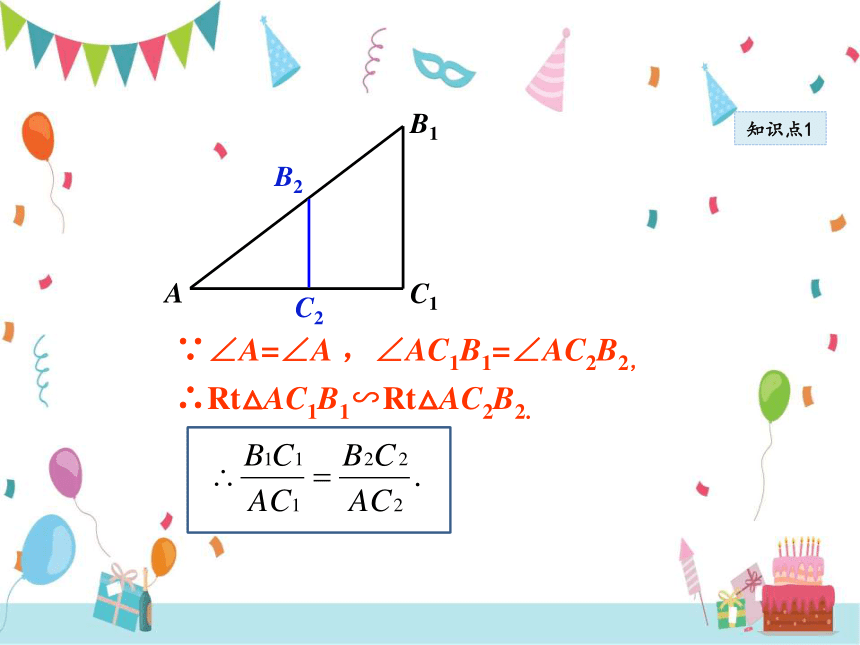

文档简介
(共34张PPT)
第一章
直角三角形的边角关系
1 锐角三角函数
(第1课时)
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念.
2.了解坡度、坡角的概念,并能用正切进行简单的计算.
学习目标
重点难点
重点:理解正切的概念.
难点:理解正切为什么能够刻画梯子的倾斜程度.
生活中的梯子
梯子是我们日常生活中常见的物体.
情境导入
你会比较两个梯子哪个更陡吗?你有哪些办法?
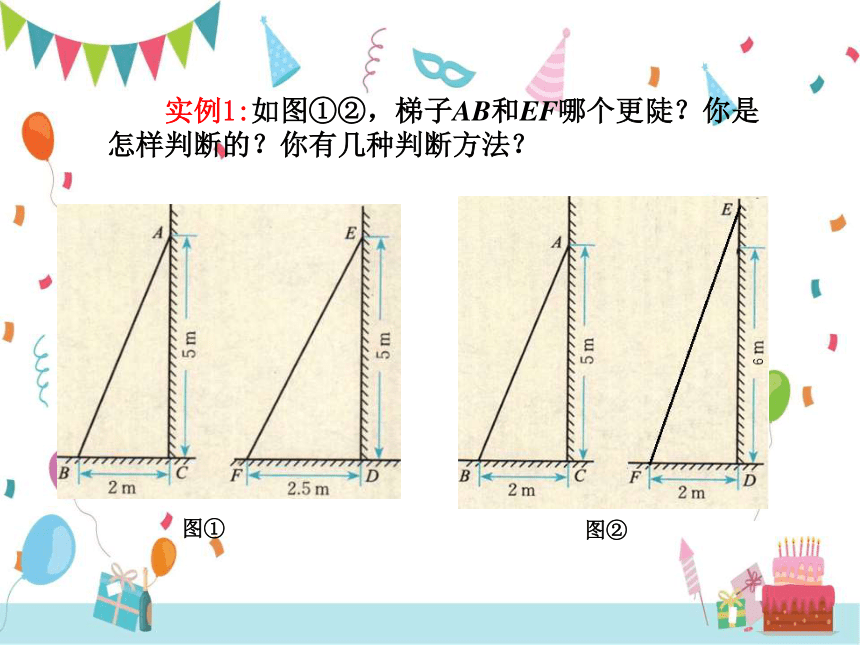
实例1:如图①②,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?
图①
图②
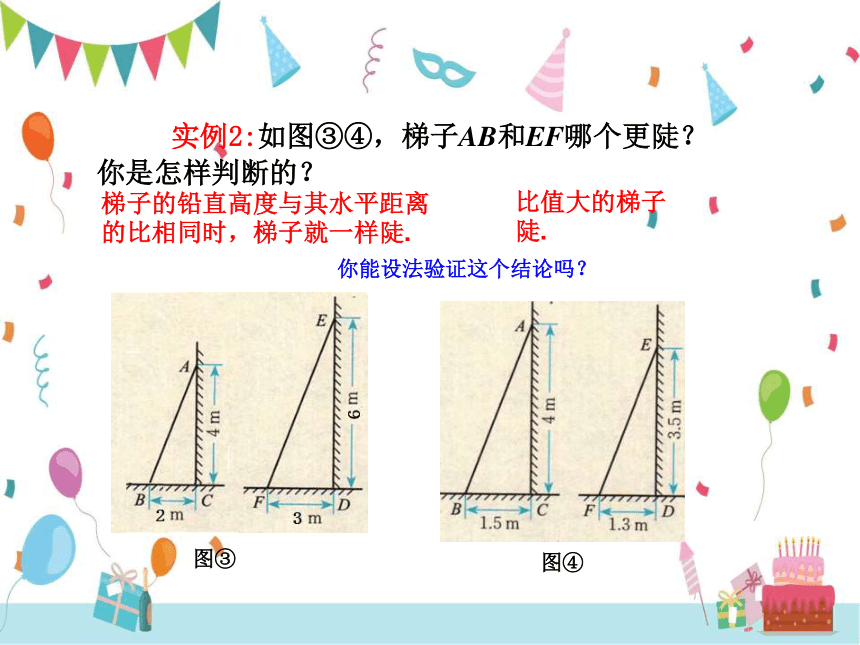
实例2:如图③④,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
图③
图④
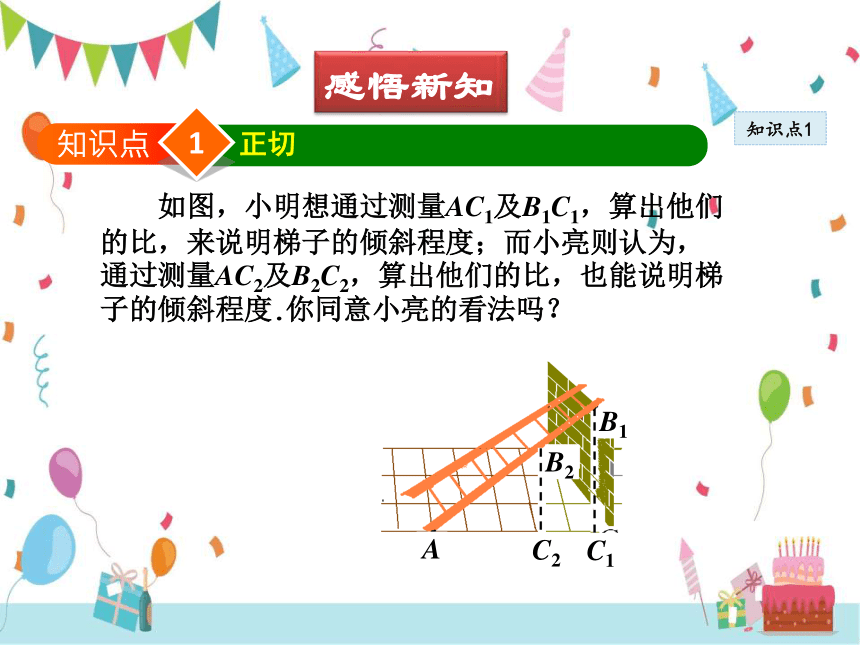
如图,小明想通过测量AC1及B1C1,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量AC2及B2C2,算出他们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
A
C2
C1
B2
B1
1
知识点
正切
知识点1
感悟新知
C2
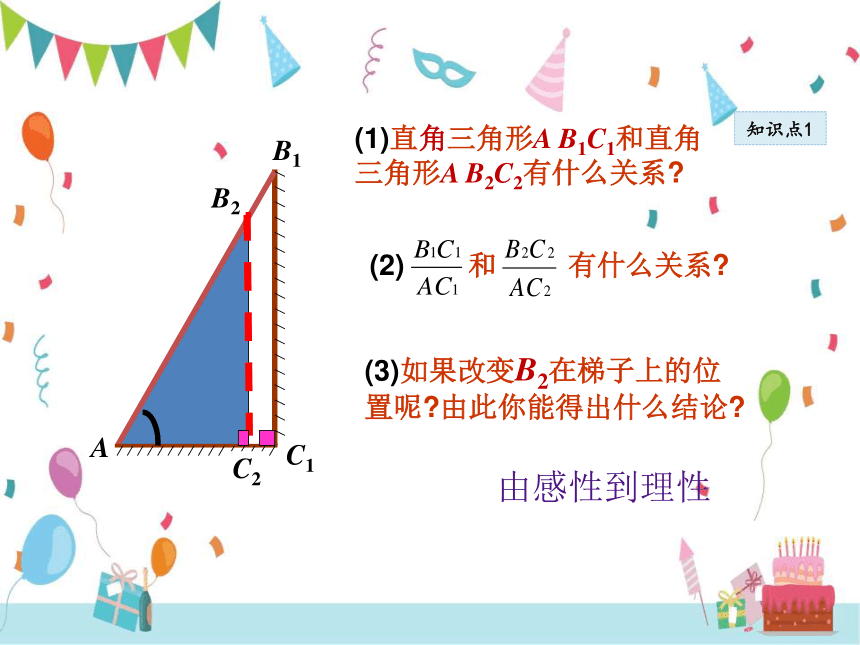
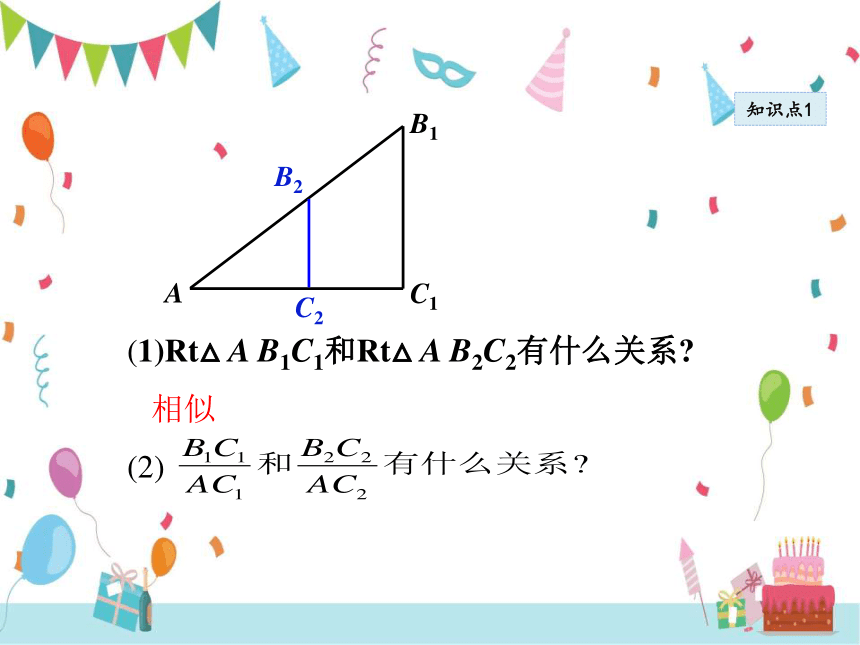
(1)直角三角形A B1C1和直角三角形A B2C2有什么关系
(2) 和 有什么关系
(3)如果改变B2在梯子上的位置呢 由此你能得出什么结论
由感性到理性
C2
C1
A
B2
B1
知识点1
(1)Rt△ A B1C1和Rt△ A B2C2有什么关系
相似
(2)
A
C2
C1
B2
B1
知识点1
∵∠A=∠A ,∠AC1B1=∠AC2B2,
∴Rt△AC1B1∽Rt△AC2B2.
A
C2
C1
B2
B1
知识点1
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的.
归 纳
知识点1
A
B
C
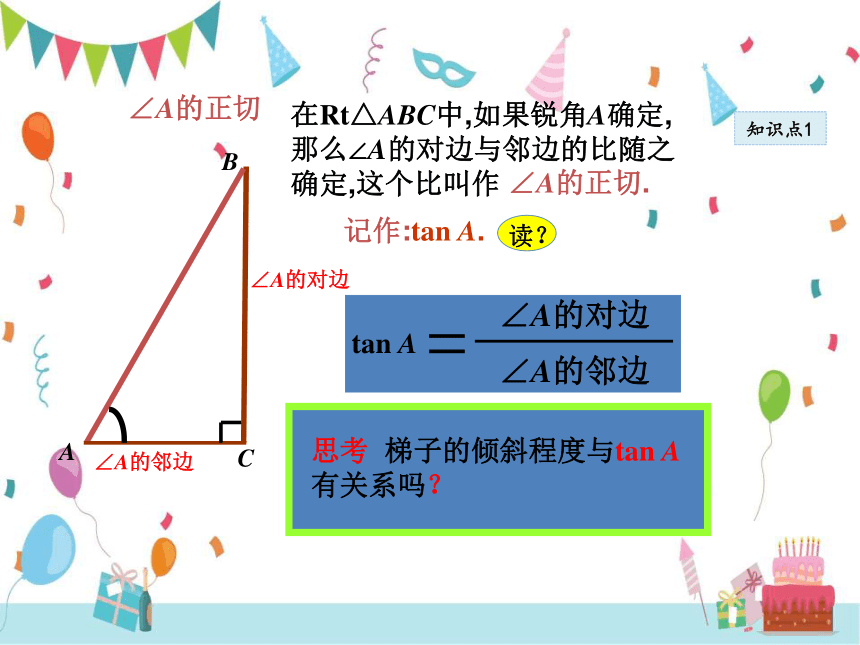
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan A
∠A的正切
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫作
∠A的正切.
记作:tan A.
读?
思考 梯子的倾斜程度与tan A有关系吗?
知识点1
(1)tan A是在直角三角形中定义的,∠A是一个锐角(注意构造直角三角形).
(2)tan A是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.
注意:
知识点1
(3)tan A是一个比值(直角边之比,注意比的顺序);且tan A ﹥0,无单位.
(4)tan A的大小只与∠A的大小有关,而与直角三角形的大小无关.
知识点1
议一议:
梯子的倾斜程度与tan B有什么关系?
tan B的值越大,梯子越陡,∠B越大.
怎样解答
A
B
C
知识点1
归 纳
(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程
度,因为夹角的正切值越大,则夹角越大,物体放
置得越“陡”.
知识点1
例1 如图表示两个自动扶梯,哪一个自动扶梯比较陡?
乙
甲
13 m
5 m
6 m
8 m
知识点1
解:甲梯中,
tan α= .
乙梯中,
tan β= .
因为tan β>tan α,所以乙梯更陡.
知识点1
例2 在△ABC中,∠C=90°,BC=12 cm,AB=20 cm,求tan A和tan B的值.
20
12
怎样解答
A
B
C
知识点1
tan A=
tan B=
.
解:在△ABC中,∠C=90°,所以AC= =16(cm),
知识点1
解题小结
直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义
求解.
知识点1
例3(桂林中考)如下图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD=________.
根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=
解析:
答案:
知识点1
解题小结
直接求某个锐角的正切值有困难时,可以考虑利
用中间量进行转化,可以是相等的角作为中间量,还
可以利用相似,得到相等的比作为中间量.
知识点1
2
知识点
坡度和坡角
探究
如图是某一大坝的横断面.
坡面AB的垂直高度与水平宽度AE的长度之比与α有什么关系?
α
A
C
B
D
E
坡面AB与水平面的夹角叫作坡角.
知识点2
正切通常也用来描述山坡的坡度.
坡度:铅直高度与水平宽度的比,记作 i ,也称为坡比.
E
F
A
B
C
D
50 m
60 m
tan A=5/6
知识点2
例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
B
知识点2
特别提醒:坡度的概念,一要记住是一个比值而不是角度,二要明确坡度其实就是坡角的正切.
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
例5 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
知识点2
1.判断对错:
(1)如图1, tan A= . ( )
(2)如图1, tan B = . ( )
图1
错
错
怎样解答
A
B
C
随堂练习
(4)如图2,tan B= . ( )
图2
(3)如图2,tan A=0.7 m. ( )
错
对
怎样解答
A
B
C
10 m
7 m
2.在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tan A的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tan C吗?
tan C=
B
A
C
D
4
1.5
4. 在等腰△ABC中,AB=AC=13,BC=10,求tan B.
tan B=12/5
13
13
10
D
5
12
B
A
C
D
5.如图,∠C=90°,CD⊥AB,则
tan B= .
CD
BD
AC
BC
AD
CD
A
B
C
D
(1)正切的定义:∠A的对边与邻边的比叫作∠A的正切,记作tan A,即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
(2)正切与坡度(角)的关系:
坡度就是坡角的正切.
课堂小结
(3)数形结合的方法;构造直角三角形的意识.
第一章
直角三角形的边角关系
1 锐角三角函数
(第1课时)
1.经历探索刻画梯子倾斜程度的过程,理解正切的概念.
2.了解坡度、坡角的概念,并能用正切进行简单的计算.
学习目标
重点难点
重点:理解正切的概念.
难点:理解正切为什么能够刻画梯子的倾斜程度.
生活中的梯子
梯子是我们日常生活中常见的物体.
情境导入
你会比较两个梯子哪个更陡吗?你有哪些办法?
实例1:如图①②,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?
图①
图②
实例2:如图③④,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
图③
图④
如图,小明想通过测量AC1及B1C1,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量AC2及B2C2,算出他们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
A
C2
C1
B2
B1
1
知识点
正切
知识点1
感悟新知
C2
(1)直角三角形A B1C1和直角三角形A B2C2有什么关系
(2) 和 有什么关系
(3)如果改变B2在梯子上的位置呢 由此你能得出什么结论
由感性到理性
C2
C1
A
B2
B1
知识点1
(1)Rt△ A B1C1和Rt△ A B2C2有什么关系
相似
(2)
A
C2
C1
B2
B1
知识点1
∵∠A=∠A ,∠AC1B1=∠AC2B2,
∴Rt△AC1B1∽Rt△AC2B2.
A
C2
C1
B2
B1
知识点1
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的.
归 纳
知识点1
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tan A
∠A的正切
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫作
∠A的正切.
记作:tan A.
读?
思考 梯子的倾斜程度与tan A有关系吗?
知识点1
(1)tan A是在直角三角形中定义的,∠A是一个锐角(注意构造直角三角形).
(2)tan A是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.
注意:
知识点1
(3)tan A是一个比值(直角边之比,注意比的顺序);且tan A ﹥0,无单位.
(4)tan A的大小只与∠A的大小有关,而与直角三角形的大小无关.
知识点1
议一议:
梯子的倾斜程度与tan B有什么关系?
tan B的值越大,梯子越陡,∠B越大.
怎样解答
A
B
C
知识点1
归 纳
(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程
度,因为夹角的正切值越大,则夹角越大,物体放
置得越“陡”.
知识点1
例1 如图表示两个自动扶梯,哪一个自动扶梯比较陡?
乙
甲
13 m
5 m
6 m
8 m
知识点1
解:甲梯中,
tan α= .
乙梯中,
tan β= .
因为tan β>tan α,所以乙梯更陡.
知识点1
例2 在△ABC中,∠C=90°,BC=12 cm,AB=20 cm,求tan A和tan B的值.
20
12
怎样解答
A
B
C
知识点1
tan A=
tan B=
.
解:在△ABC中,∠C=90°,所以AC= =16(cm),
知识点1
解题小结
直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利
用勾股定理求出未知的直角边,再利用正切的定义
求解.
知识点1
例3(桂林中考)如下图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD=________.
根据题意得∠BCD=∠CAB,
所以tan ∠BCD=tan ∠CAB=
解析:
答案:
知识点1
解题小结
直接求某个锐角的正切值有困难时,可以考虑利
用中间量进行转化,可以是相等的角作为中间量,还
可以利用相似,得到相等的比作为中间量.
知识点1
2
知识点
坡度和坡角
探究
如图是某一大坝的横断面.
坡面AB的垂直高度与水平宽度AE的长度之比与α有什么关系?
α
A
C
B
D
E
坡面AB与水平面的夹角叫作坡角.
知识点2
正切通常也用来描述山坡的坡度.
坡度:铅直高度与水平宽度的比,记作 i ,也称为坡比.
E
F
A
B
C
D
50 m
60 m
tan A=5/6
知识点2
例4 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
错解分析:概念不清,误以为坡度是一个角度,而猜测
坡度即为倾斜角的度数.
B
知识点2
特别提醒:坡度的概念,一要记住是一个比值而不是角度,二要明确坡度其实就是坡角的正切.
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
例5 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
知识点2
1.判断对错:
(1)如图1, tan A= . ( )
(2)如图1, tan B = . ( )
图1
错
错
怎样解答
A
B
C
随堂练习
(4)如图2,tan B= . ( )
图2
(3)如图2,tan A=0.7 m. ( )
错
对
怎样解答
A
B
C
10 m
7 m
2.在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tan A的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tan C吗?
tan C=
B
A
C
D
4
1.5
4. 在等腰△ABC中,AB=AC=13,BC=10,求tan B.
tan B=12/5
13
13
10
D
5
12
B
A
C
D
5.如图,∠C=90°,CD⊥AB,则
tan B= .
CD
BD
AC
BC
AD
CD
A
B
C
D
(1)正切的定义:∠A的对边与邻边的比叫作∠A的正切,记作tan A,即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
(2)正切与坡度(角)的关系:
坡度就是坡角的正切.
课堂小结
(3)数形结合的方法;构造直角三角形的意识.
