冀教版 数学四年级下册 4.3 三角形内角和课件 (共13张PPT)
文档属性
| 名称 | 冀教版 数学四年级下册 4.3 三角形内角和课件 (共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 17:08:54 | ||
图片预览




文档简介
(共13张PPT)
三角形内角和
情境导入
探究新知
课堂小结
课后作业
多边形的认识
课堂练习
4
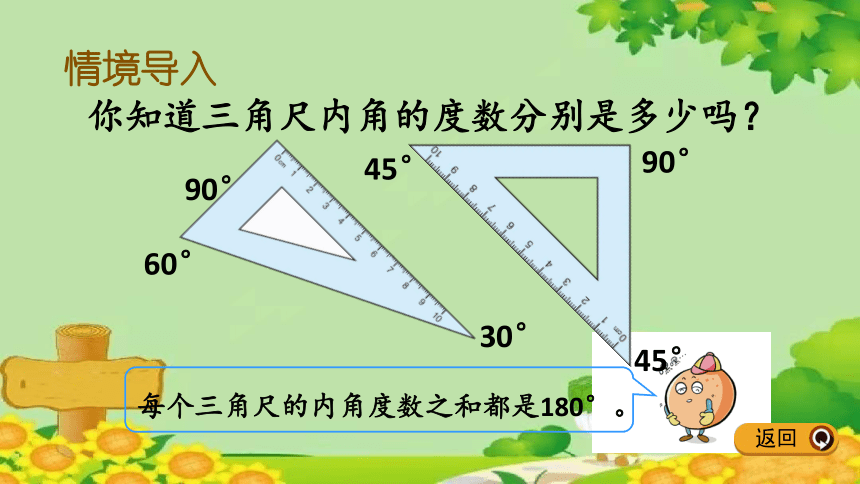
每个三角尺的内角度数之和都是180°。
30°
60°
90°
45°
90°
45°
情境导入
返回
你知道三角尺内角的度数分别是多少吗?
例 1
(1)观察下面两个特殊的三角形,
猜猜:它们的角有什么特点?
探究新知
返回
等腰三角形两条腰相等,两个底角相等 。
等边三角形三条边相等,三个角都相等 。
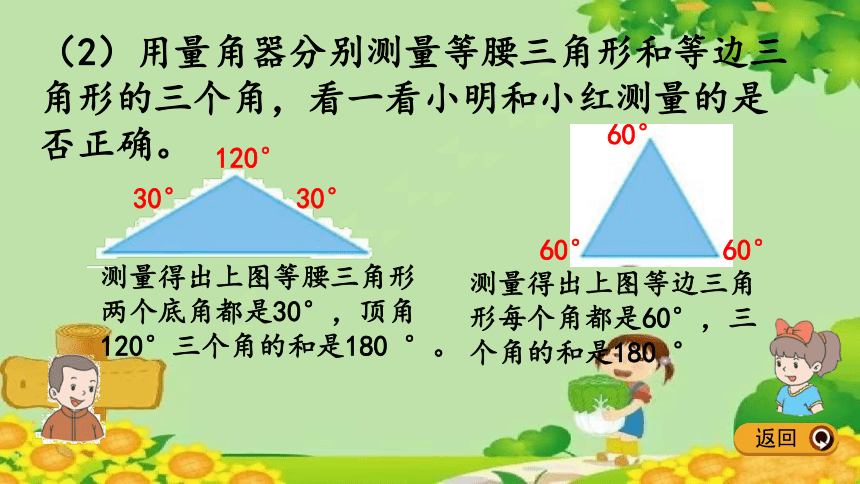
(2)用量角器分别测量等腰三角形和等边三角形的三个角,看一看小明和小红测量的是否正确。
30°
30°
60°
60°
120°
60°
返回
测量得出上图等腰三角形
两个底角都是30°,顶角
120°三个角的和是180 °。
测量得出上图等边三角
形每个角都是60°,三
个角的和是180 °
(1)任意画一个三角形,测量并记录三个内角的度数。
2
3
1
∠1, ∠2, ∠3都叫做三角形的内角。
∠1+ ∠2+ ∠3=三角形内角和。
返回
例 2
(2)把小组内几个同学的测量结果进行统计,并计算内角的和。
测量发现:任意三角形的内角和都是180°。
有什么方法能验证你们的想法?想一想,做一做。
3
2
3
1
平角:180°
返回
(1)直角三角形中两个锐角的和是多少度?
30°
60°
90°
45°
90°
45°
60°+30°=90° 45°+45°=90°
两个锐角的和:180°-90°=90°
返回
(2)一个三角形至少有几个锐角?为什么?
假设只有1个锐角,那就会有2个直角或钝角,这时三角形的内角和会超过180°。
假设有2个锐角,那要保证内角和是180°,第三个角可以是锐角、钝角、直角的任何一种。
假设没有锐角,2个直角的和就已经是180°了,不能再加第三个角,所以不符合。
所以一个三角形至少有2个锐角。
返回
填出下面各角的度数。
77°
55°
115°
180°-75°-28°=77°
180°-90°-35°=55°
180°-45°-20°=77°
课堂练习
返回
(1) ∠1=50°,∠2=35°,∠3=( )。
这是一个( )角三角形。
(2) ∠1=42°,∠2=48°,∠3=( )。
这是一个( )角三角形。
(3) ∠1=70°,∠2=55°,∠3=( )。
这是一个( )角三角形,也是一个( )三角形。
95°
钝
90°
直
55°
锐
等腰
算一算,判一判。∠1,∠2,∠3是三角形的三个内角。
返回
1.三角形的内角和:三角形的三个内角的和叫做三角形的内角和。
2.直角三角形中两个锐角的和是90°。一个三角形至少有两个锐角。
这节课你们都学会了哪些知识?
课堂小结
返回
课本:
第37页第1、2题
返回
课后作业
三角形内角和
情境导入
探究新知
课堂小结
课后作业
多边形的认识
课堂练习
4
每个三角尺的内角度数之和都是180°。
30°
60°
90°
45°
90°
45°
情境导入
返回
你知道三角尺内角的度数分别是多少吗?
例 1
(1)观察下面两个特殊的三角形,
猜猜:它们的角有什么特点?
探究新知
返回
等腰三角形两条腰相等,两个底角相等 。
等边三角形三条边相等,三个角都相等 。
(2)用量角器分别测量等腰三角形和等边三角形的三个角,看一看小明和小红测量的是否正确。
30°
30°
60°
60°
120°
60°
返回
测量得出上图等腰三角形
两个底角都是30°,顶角
120°三个角的和是180 °。
测量得出上图等边三角
形每个角都是60°,三
个角的和是180 °
(1)任意画一个三角形,测量并记录三个内角的度数。
2
3
1
∠1, ∠2, ∠3都叫做三角形的内角。
∠1+ ∠2+ ∠3=三角形内角和。
返回
例 2
(2)把小组内几个同学的测量结果进行统计,并计算内角的和。
测量发现:任意三角形的内角和都是180°。
有什么方法能验证你们的想法?想一想,做一做。
3
2
3
1
平角:180°
返回
(1)直角三角形中两个锐角的和是多少度?
30°
60°
90°
45°
90°
45°
60°+30°=90° 45°+45°=90°
两个锐角的和:180°-90°=90°
返回
(2)一个三角形至少有几个锐角?为什么?
假设只有1个锐角,那就会有2个直角或钝角,这时三角形的内角和会超过180°。
假设有2个锐角,那要保证内角和是180°,第三个角可以是锐角、钝角、直角的任何一种。
假设没有锐角,2个直角的和就已经是180°了,不能再加第三个角,所以不符合。
所以一个三角形至少有2个锐角。
返回
填出下面各角的度数。
77°
55°
115°
180°-75°-28°=77°
180°-90°-35°=55°
180°-45°-20°=77°
课堂练习
返回
(1) ∠1=50°,∠2=35°,∠3=( )。
这是一个( )角三角形。
(2) ∠1=42°,∠2=48°,∠3=( )。
这是一个( )角三角形。
(3) ∠1=70°,∠2=55°,∠3=( )。
这是一个( )角三角形,也是一个( )三角形。
95°
钝
90°
直
55°
锐
等腰
算一算,判一判。∠1,∠2,∠3是三角形的三个内角。
返回
1.三角形的内角和:三角形的三个内角的和叫做三角形的内角和。
2.直角三角形中两个锐角的和是90°。一个三角形至少有两个锐角。
这节课你们都学会了哪些知识?
课堂小结
返回
课本:
第37页第1、2题
返回
课后作业
