数学高中苏教版选修(2-3)2.4《二项分布》课件1
文档属性
| 名称 | 数学高中苏教版选修(2-3)2.4《二项分布》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-01 00:00:00 | ||
图片预览






文档简介
课件14张PPT。2.4二项分布教学目标:
1、理解n次独立重复试验的模型( n重复伯努利试验)及其意义;
2、理解二项分布,并能解决一些简单的实际问题§2.4 二项分布什么叫做X服从参数为n,p的二项分布?
用符号如何表示?本节课的教学目标
——如何回答以下这些问题?请用3分钟快速阅读课本,然后回答以上问题 我们称这样的随机变量ξ服从二项分布,记作 ,其中n,p为参数,并记 如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中这个事件恰好发生k次的概率是多少?在这个试验中,随机变量是什么?二项分布其中k = 0,1,…,n .p = 1- q.于是得到随机变量ξ的概率分布如下:请大家打开教材阅读二项分布的引入部分
看自己是否理解何为二项分布?应用二项分布解决实际问题的步骤:
(1)判断问题是否为独立重复试验;
(2)在不同的实际问题中找出概率模型
中的n、k、p;
(3)运用公式求概率. 打开教材阅读第61-62页上的例题1、2
注意:理解解答过程、学习解题格式例1. 1名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在交通岗遇到红灯的事件是独立的,并且概率都是1/3.(1)求这名学生在途中遇到红灯的次数ξ的分布列.(2)求这名学生在途中至少遇到一次红灯的概率.解:(2)至少遇到一次红灯的概率为
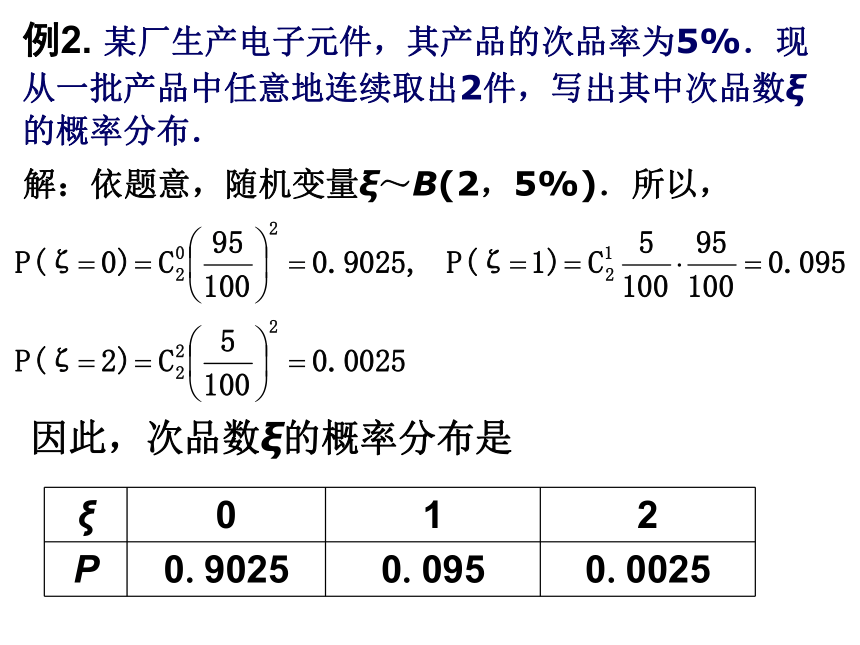
例2. 某厂生产电子元件,其产品的次品率为5%.现
从一批产品中任意地连续取出2件,写出其中次品数ξ
的概率分布.解:依题意,随机变量ξ~B(2,5%).所以,因此,次品数ξ的概率分布是问题: 在一袋中装有一只红球和九只白球,每次从袋中任取一球取后放回,直到取得红球为止,求取球次数ξ的分布.分析:袋中虽然只有10个球,由于每次任取一球,取后又放回,因此应注意以下几点:
(1)一次取球两个结果:取红球A或取白球ā,且P(A)=0.1;
(2)取球次数ξ可能取1,2,…;
(3)由于取后放回.因此,各次取球相互独立.于是得到随机变量ξ的概率分布如下:称ξ服从几何分布,并记 g (k , p) = p·qk-1在独立重复试验中,某事件A第一次发生时所作的试验
次数ξ也是一个取值为正整数的随机变量. “ξ =k”表
示在第k次独立重复试验时事件 A 第一次发生.如果把
第k次实验时事件A发生记为 A k, p( A k )=p,那么例 3. 某人射击击中目标的概率是0.2,射击中每次射击
的结果是相互独立的,求他在10次射击中击中目标的
次数不超过5次的概率(精确到0.01).解:设在这10次射击中击中目标的次数是ξ,则
ξ~B(10,0.2).答:他在10次射击中击中目标的次数不超过5次的概率为0.99.例4. 某人每次投篮投中的概率为 0.1,各次投篮的结果互相独立 .求他首次投篮投中时投篮次数的分布列以及他在5次内投中的概率(精确到0.01).解:设他首次投篮投中时投篮的次数是ξ,则ξ服从几何
分布,其中p = 0.1,ξ的分布列为答:他在5次内投中的概率为0.41.例5. 某射手有5发子弹,射击一次命中的概率为0.9
⑴如果命中了就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.
⑵如果命中2次就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.解:⑴的所有取值为:1、2、3、4、5表示第一次就射中,它的概率为:表示第一次没射中,第二次射中,∴同理表示前四次都没射中,∴注意学习此题解答方法和书写格式!某射手有5发子弹,射击一次命中的概率为0.9.⑴如果命中了就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布列.⑵如果命中2次就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.解:⑵的所有取值为:2、3、4、5表示前二次都射中,它的概率为:表示前二次恰有一次射中,第三次射中,∴表示前四次中恰有一次射中,或前四次全部没射中 同理 注意学习此题解答方法和书写格式! 从一批有10个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同,在下列三种情况下,分别求出直到取出合格品为止时所需抽取的次数 的分布.解:表示只取一次就取到合格品表示第一次取到次品,第二次取到合格品表示第一、二次都取到次品,第三次取到合格品∴随机变量的分布为:的所有取值为:1、2、3、4.每次取出的产品都不放回此批产品中;注意学习此题解答方法和书写格式!一、理解n次独立重复试验的模型(n重伯努利试验)及其意义课堂小结作业:
课本: P64 8、10、11
步步高课时作业: P33-36 2. 4二项分布(一)、(二)
自选强化练习:优化方案相应部分
复习计数原理、排列、组合、二项式定理二、理解理解二项分布,并能解决一些简单的实际问题.
1、理解n次独立重复试验的模型( n重复伯努利试验)及其意义;
2、理解二项分布,并能解决一些简单的实际问题§2.4 二项分布什么叫做X服从参数为n,p的二项分布?
用符号如何表示?本节课的教学目标
——如何回答以下这些问题?请用3分钟快速阅读课本,然后回答以上问题 我们称这样的随机变量ξ服从二项分布,记作 ,其中n,p为参数,并记 如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中这个事件恰好发生k次的概率是多少?在这个试验中,随机变量是什么?二项分布其中k = 0,1,…,n .p = 1- q.于是得到随机变量ξ的概率分布如下:请大家打开教材阅读二项分布的引入部分
看自己是否理解何为二项分布?应用二项分布解决实际问题的步骤:
(1)判断问题是否为独立重复试验;
(2)在不同的实际问题中找出概率模型
中的n、k、p;
(3)运用公式求概率. 打开教材阅读第61-62页上的例题1、2
注意:理解解答过程、学习解题格式例1. 1名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在交通岗遇到红灯的事件是独立的,并且概率都是1/3.(1)求这名学生在途中遇到红灯的次数ξ的分布列.(2)求这名学生在途中至少遇到一次红灯的概率.解:(2)至少遇到一次红灯的概率为
例2. 某厂生产电子元件,其产品的次品率为5%.现
从一批产品中任意地连续取出2件,写出其中次品数ξ
的概率分布.解:依题意,随机变量ξ~B(2,5%).所以,因此,次品数ξ的概率分布是问题: 在一袋中装有一只红球和九只白球,每次从袋中任取一球取后放回,直到取得红球为止,求取球次数ξ的分布.分析:袋中虽然只有10个球,由于每次任取一球,取后又放回,因此应注意以下几点:
(1)一次取球两个结果:取红球A或取白球ā,且P(A)=0.1;
(2)取球次数ξ可能取1,2,…;
(3)由于取后放回.因此,各次取球相互独立.于是得到随机变量ξ的概率分布如下:称ξ服从几何分布,并记 g (k , p) = p·qk-1在独立重复试验中,某事件A第一次发生时所作的试验
次数ξ也是一个取值为正整数的随机变量. “ξ =k”表
示在第k次独立重复试验时事件 A 第一次发生.如果把
第k次实验时事件A发生记为 A k, p( A k )=p,那么例 3. 某人射击击中目标的概率是0.2,射击中每次射击
的结果是相互独立的,求他在10次射击中击中目标的
次数不超过5次的概率(精确到0.01).解:设在这10次射击中击中目标的次数是ξ,则
ξ~B(10,0.2).答:他在10次射击中击中目标的次数不超过5次的概率为0.99.例4. 某人每次投篮投中的概率为 0.1,各次投篮的结果互相独立 .求他首次投篮投中时投篮次数的分布列以及他在5次内投中的概率(精确到0.01).解:设他首次投篮投中时投篮的次数是ξ,则ξ服从几何
分布,其中p = 0.1,ξ的分布列为答:他在5次内投中的概率为0.41.例5. 某射手有5发子弹,射击一次命中的概率为0.9
⑴如果命中了就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.
⑵如果命中2次就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.解:⑴的所有取值为:1、2、3、4、5表示第一次就射中,它的概率为:表示第一次没射中,第二次射中,∴同理表示前四次都没射中,∴注意学习此题解答方法和书写格式!某射手有5发子弹,射击一次命中的概率为0.9.⑴如果命中了就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布列.⑵如果命中2次就停止射击,否则一直射击到子弹用完,求耗用子弹数 的分布.解:⑵的所有取值为:2、3、4、5表示前二次都射中,它的概率为:表示前二次恰有一次射中,第三次射中,∴表示前四次中恰有一次射中,或前四次全部没射中 同理 注意学习此题解答方法和书写格式! 从一批有10个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同,在下列三种情况下,分别求出直到取出合格品为止时所需抽取的次数 的分布.解:表示只取一次就取到合格品表示第一次取到次品,第二次取到合格品表示第一、二次都取到次品,第三次取到合格品∴随机变量的分布为:的所有取值为:1、2、3、4.每次取出的产品都不放回此批产品中;注意学习此题解答方法和书写格式!一、理解n次独立重复试验的模型(n重伯努利试验)及其意义课堂小结作业:
课本: P64 8、10、11
步步高课时作业: P33-36 2. 4二项分布(一)、(二)
自选强化练习:优化方案相应部分
复习计数原理、排列、组合、二项式定理二、理解理解二项分布,并能解决一些简单的实际问题.
